
- •Глава 5. Уравнения первого порядка, не разрешенные относительно производной.
- •§ 1. Общие положения.
- •§ 2. Уравнения 1-го порядка: многочлен - ой степени относительно символа .
- •§ 3. Уравнение, разрешенное относительно y и не содержащее X.
- •§ 4. Уравнение, разрешенное относительно X и не содержащее y.
- •§ 5. Уравнение, не разрешенное относительно y и не содержащее X.
- •§ 6. Уравнение, не разрешенное относительно X и не содержащее y.
- •§ 7. Уравнение Лагранжа.
- •§ 7. Применение уравнений первого порядка, не разрешенных относительно производной: задачи из геометрии
- •§ 8. Применение уравнений первого порядка, не разрешенных относительно производной: задачи из физики
§ 3. Уравнение, разрешенное относительно y и не содержащее X.
Из
названия параграфа следует, что
дифференциальное уравнение имеет вид:
![]() .
Для решения таких уравнений разработан
специальный способ – поиск решения в
параметрической форме:
.
Для решения таких уравнений разработан
специальный способ – поиск решения в
параметрической форме:
1). Примем:
![]() =
=![]() ,
то есть
,
то есть
![]() .
Перепишем исходное уравнение:
.
Перепишем исходное уравнение:
![]() .
Так как
.
Так как
![]() есть некоторая функция переменной
есть некоторая функция переменной
![]() ,
то и
,
то и
![]() .
.
2). Имея:
![]() ,
запишем
,
запишем
![]() .
В то же время
.
В то же время
![]() .
Учитывая оба выражения для дифференциала
.
Учитывая оба выражения для дифференциала
![]() ,
нетрудно записать:
,
нетрудно записать:
![]() =
=![]() – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
3). Учтём
решение
![]() ,
то есть
,
то есть
![]() =0.
Принимая
=0.
Принимая
![]() ,
можем записать:
,
можем записать:
![]() =
=![]() .
Интегрируя последнее, получаем:
.
Интегрируя последнее, получаем:
![]() =
=![]() .
.
4).
Составим систему:
![]() – это параметрическое решение уравнения
– это параметрическое решение уравнения
![]() .
.
☺☺
Пример 5–02:
Найти общее решение уравнения:
![]() в параметрической форме.
в параметрической форме.
Решение:
1). Форма
записи уравнения имеет вид:
![]() .
Примем:
.
Примем:
![]() =
=![]() ,
то есть
,
то есть
![]() .
Перепишем исходное уравнение:
.
Перепишем исходное уравнение:
![]() =
=![]() .
Так как
.
Так как
![]() есть некоторая функция переменной
есть некоторая функция переменной
![]() ,
то и
,
то и
![]() .
.
2). Имея:
![]() ,
запишем
,
запишем
![]() ,
где
,
где
![]() =
=![]() .
В то же время
.
В то же время
![]() .
Учитывая оба выражения для дифференциала
.
Учитывая оба выражения для дифференциала
![]() ,
нетрудно записать:
,
нетрудно записать:
![]() =
=![]() .
В нашем случае:
.
В нашем случае:
![]() =
=![]() – уравнение с разделяющимися переменными!
– уравнение с разделяющимися переменными!
3). Учитывая,
что
![]() ,
можем записать:
,
можем записать:
![]() =
=![]() ,
которое легко интегрируется:
,
которое легко интегрируется:
![]() =
=![]() ,
то есть
,
то есть
![]() =
=![]() .
.
4). Составим
систему:
![]() ,
или
,
или
![]() –
это параметрическое решение.
–
это параметрическое решение.
Замечание:
Можно было бы попробовать выразить из
системы решение в виде:
![]() .
Так как для нас важнее освоение самого
метода параметрического решения, то
дальнейшие алгебраические упражнения
советуем не выполнять!..
.
Так как для нас важнее освоение самого
метода параметрического решения, то
дальнейшие алгебраические упражнения
советуем не выполнять!..
Ответ:
общее решение:
![]() в параметрической форме.
в параметрической форме.
Пример 5–03:
Найти общее решение уравнения:
![]() в параметрической форме.
в параметрической форме.
Решение:
1). Форма
записи уравнения имеет вид:
![]() .
Примем:
.
Примем:
![]() =
=![]() ,
то есть
,
то есть
![]() .
Перепишем исходное уравнение:
.
Перепишем исходное уравнение:
![]() =
=![]() .
Так как
.
Так как
![]() есть некоторая функция переменной
есть некоторая функция переменной
![]() ,
то и
,
то и
![]() .
.
2). Имея:
![]() ,
запишем
,
запишем
![]() ,
где
,
где
![]() =
=![]() .
В то же время
.
В то же время
![]() .
Учитывая оба выражения для дифференциала
.
Учитывая оба выражения для дифференциала
![]() ,
нетрудно записать:
,
нетрудно записать:
![]() =
=![]() .
В нашем случае:
.
В нашем случае:
![]() =
=![]() – уравнение с разделяющимися переменными!
– уравнение с разделяющимися переменными!
3). Учтём
решение
![]() ,
то есть
,
то есть
![]() .
Принимая
.
Принимая
![]() ,
можем записать:
,
можем записать:
![]() =
=![]() .
.
4). Запишем:
![]() =
=![]() +
+![]() +
+![]() =
=![]() .
Вычислим
.
Вычислим
![]() =
=![]()
![]() ;
применим замену:
;
применим замену:
![]() и запишем
и запишем
![]() =
=![]()
![]() ;
применим замену:
;
применим замену:
![]() и запишем
и запишем
![]() =
=![]() =
=![]() =
=![]() =
=![]() ;
используя замену
;
используя замену
![]() ,
запишем окончательно:
,
запишем окончательно:
![]() =
=
![]() .
Что касается вычисления интеграла
.
Что касается вычисления интеграла
![]() ,
то здесь применением замены:
,
то здесь применением замены:
![]() сразу можем записать:
сразу можем записать:
![]() =
=![]() .
.
5). Окончательное
выражение для неизвестной
![]() имеет
вид:
имеет
вид:
![]() =
=![]() +
+![]() +
+![]() .
.
6). Составим
систему:
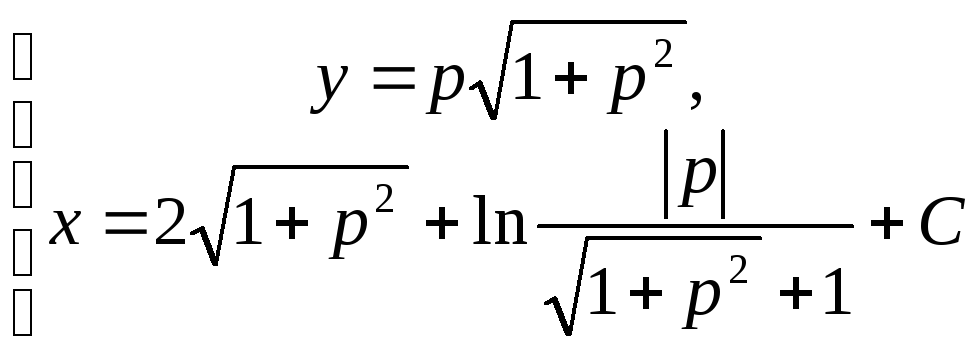 –
это параметрическое решение.
–
это параметрическое решение.
Замечание:
Можно было бы попробовать выразить из
системы решение в виде:
![]() .
В нашем случае лучше не пробовать: не
получится!..
.
В нашем случае лучше не пробовать: не
получится!..
Ответ:
 –
общее решение в параметрической форме,
также решение
–
общее решение в параметрической форме,
также решение
![]() .
.
☻
§ 4. Уравнение, разрешенное относительно X и не содержащее y.
Из
названия параграфа следует, что
дифференциальное уравнение имеет вид:
![]() .
Для решения таких уравнений разработан
специальный способ – поиск решения в
параметрической форме:
.
Для решения таких уравнений разработан
специальный способ – поиск решения в
параметрической форме:
1). Примем:
![]() =
=![]() ,
то есть
,
то есть
![]() .
Перепишем исходное уравнение:
.
Перепишем исходное уравнение:
![]() .
Так как
.
Так как
![]() есть некоторая функция переменной
есть некоторая функция переменной
![]() ,
то и
,
то и
![]() .
.
2). Имея:
![]() ,
запишем
,
запишем
![]() .
В то же время
.
В то же время
![]() .
Учитывая оба выражения для дифференциала
.
Учитывая оба выражения для дифференциала
![]() ,
нетрудно записать:
,
нетрудно записать:
![]() =
=![]() – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
3).
Интегрируя уравнение:
![]() =
=![]() получаем:
получаем:
![]() =
=![]() .
.
4).
Составим систему:
![]() – это параметрическое решение уравнения
– это параметрическое решение уравнения
![]() .
.
☺☺
Пример 5–04:
Найти общее решение уравнения:
![]() в параметрической форме.
в параметрической форме.
Решение:
1). Форма
записи уравнения имеет вид:
![]() .
Примем:
.
Примем:
![]() =
=![]() ,
то есть
,
то есть
![]() .
Перепишем исходное уравнение:
.
Перепишем исходное уравнение:
![]() =
=![]() .
.
2). Имея:
![]() ,
запишем
,
запишем
![]() ,
где
,
где
![]() =
=![]() .
В то же время
.
В то же время
![]() ,
или:
,
или:
![]() =
=![]() .
В нашем случае:
.
В нашем случае:
![]() =
=![]() – уравнение с разделёнными переменными!
– уравнение с разделёнными переменными!
3). Интегрируем
уравнение:
![]() =
=![]() =
=![]() ,
или
,
или
![]() =
=![]() .
.
4). Составим
систему:
![]() ,
или
,
или
 –
это параметрическое решение.
–
это параметрическое решение.
Замечание:
Можно было бы попробовать выразить из
системы решение в виде:
![]() .
В нашем случае лучше не пробовать!..
.
В нашем случае лучше не пробовать!..
Ответ:
 – общее решение в параметрической
форме.
– общее решение в параметрической
форме.
Пример 5–05:
Найти общее решение уравнения:
![]() в параметрической форме.
в параметрической форме.
Решение:
1). Форма
записи уравнения имеет вид:
![]() .
Примем:
.
Примем:
![]() =
=![]() ,
то есть
,
то есть
![]() .
Перепишем исходное уравнение:
.
Перепишем исходное уравнение:
![]() =
=![]() .
.
2). Имея:
![]() ,
запишем
,
запишем
![]() ,
где
,
где
![]() =
=![]() .
В то же время
.
В то же время
![]() ,
или:
,
или:
![]() =
=![]() .
В нашем случае:
.
В нашем случае:
![]() =
=![]() – уравнение с разделёнными переменными!
– уравнение с разделёнными переменными!
3). Интегрируем
уравнение:
![]() =
=![]() +
+![]() =
=![]() –
–![]() +
+![]() .
Представив
.
Представив
![]() =
=![]() ,
вычислим отдельно
,
вычислим отдельно
![]() и
и
![]() .
Первый:
.
Первый:
![]() =
=![]() (его обычно имеют в таблице интегралов!).
Второй:
(его обычно имеют в таблице интегралов!).
Второй:
![]() =
=![]() – его получают интегрированием по
частям.
– его получают интегрированием по
частям.
4). Составим
систему:
![]() – это параметрическое решение.
– это параметрическое решение.
Ответ:
![]() – общее решение в параметрической
форме.
– общее решение в параметрической
форме.
☻
