§ 2. Однородные уравнения первого порядка.

Однородные дифференциальные уравнения интересны тем, что достаточно просто приводятся к уравнениям с разделяющимися переменными, то есть всегда интегрируются.

Определение: (2.2)

Дифференциальное уравнение называется однородным, если: : В записи уравнения: функция – однородная порядка =0. : В записи уравнения: функции и – однородные одного порядка.

По отношению к каждому из указанных типов уравнений рассмотрим две задачи:

▪ задача-1: определить тип заданного уравнения;

▪ задача-2: разработать общий алгоритм решения уравнения.

Задача-1.

Заметим, определение типа конкретного дифференциального уравнения важно: это позволяет выбрать стандартный алгоритм решения уравнения и не тратить время на его обоснование в каждом решаемом Примере. Для однородных уравнений: ирассмотрим несколько примеров решения Задачи-1.

☺☺

Пример 2–04: Из заданного набора ДУ выделите однородные уравнения: а) ;

б) ; в) .

Решение:

1). Если учесть, что для заданной формы уравнения правая часть уравнения должна быть функцией нулевого порядка, то для указанных случаев получим:

а) правая часть уравнения не есть однородная функция;

б) правая часть уравнения – однородная функция нулевого порядка;

в) правая часть уравнения – однородная функция нулевого порядка.

2). Следовательно, в случаях б) и в) заданные уравнения – однородные.

Ответ: уравнения б) и в) – однородные.

Пример 2–05: Из заданных уравнений: а) =0; б) =0; в) =0 выделите однородные уравнения.

Решение:

1). Если учесть, что для заданной формы уравнения требуется, чтобы функции и были однородными одинакового порядка, то для указанных случаев получим:

а) функции и – однородные и обе имеют порядок 1;

б) функции и – однородные и обе имеют порядок 0;

в) функция – однородная нулевого порядка, функция – неоднородная.

2). Следовательно, в случаях а) и б) заданные уравнения – однородные.

Ответ: уравнения а) и б) – однородные.

Замечание: будем считать, что однородные уравнения имеют стандартную форму записи, если уравнение представлено в виде выражения: .

Пример 2–06: Из заданных уравнений: а) ; б) ; в) ; г) выделите однородные уравнения, имеющие стандартную форму записи.

Решение:

1). Учитывая определение стандартной формы однородного уравнения, для указанных случаев получим: а) запись уравнения не соответствует стандартной форме;

б) запись уравнения соответствует стандартной форме;

в) запись уравнения не соответствует стандартной форме;

г) запись уравнения соответствует стандартной форме.

2). Следовательно, в случаях б) и г) заданные уравнения записаны в стандартной форме.

Ответ: стандартную форму записи имеют только уравнения: б) и г).

☻

Задача-2, вариант:.

Требуется решить однородное уравнение, заданное в виде: –исходнаязапись. При рассмотрении однородных функций нулевого порядка было показано, как привести однородную функциюк виду. Это позволяет (применяя тождественные преобразования) получитьстандартнуюзапись однородного уравнения:. Используя исходную и стандартную записи однородного уравнения, получимстандартный алгоритмрешения уравнения:

1). Выделяем очевидные решения исходного уравнения. Если =0, то есть одно из решений уравнения: – прямая, параллельная оси .

2). Примем , откуда . Учитывая определение решения уравнения, потребуем, чтобы функция была решением заданного уравнения. Найдём производную: . Подставив и в уравнение , получим уравнение: . (1)

3). Нетрудно заметить, что уравнение (1) – уравнение с разделяющимися переменными, решение которого подробно рассматривается в Главе 1.

4). Уравнение (1) может иметь очевидные решения из условия: . Если =0, то функция – тоже решение (прямая, проходящая через начало координат).

5). Принимая , перепишем уравнение (1) в виде: – уравнение с разделёнными переменными, которое можно интегрировать: – общее решение уравнения (1).

6). Учитывая , получим общее решение исходного уравнения.

Замечание: Записывая общий ответ конкретного Примера, необходимо указать также возможные решения исходного уравнения: и .

☺☺

Пример 2–07: Решить дифференциальное уравнение: =.

Решение:

1). Отмечаем: очевидных решений исходного уравнения нет. Нетрудно заметить, что правая часть уравнения есть однородная функция нулевого порядка. Запишем: == и применим стандартный алгоритм решения уравнения.

2). Примем и запишем: ===. Из условия: получаем решение: . Учитывая , получаем частные решения заданного уравнения в виде: – прямые, проходящих через начало координат .

3). Принимая , запишем: – общее решение уравнения. В нашем случае: . Нетрудно заметить, что . Общее решение заданного уравнения запишем в виде: , где .

Ответ: общее решение уравнения: , также .

Пример 2–08: Решить дифференциальное уравнение: =.

Решение:

Замечание: Так как переменная может принимать значения: и , рассмотрим оба случая!

Случай-1: .

1). Отмечаем: очевидных решений исходного уравнения нет. Учитывая , заданное уравнение представим в виде: == и применим стандартный алгоритм решения уравнения.

2). Примем и запишем: =. Из условия: получаем решение: . Учитывая , получаем частные решения заданного уравнения в виде: – две прямые, проходящие через начало координат .

3). Принимая , запишем: – общее решение уравнения. В нашем случае: , или: , где . Из соображений удобства, можно записать общее решение в виде:

Ответ: общее решение уравнения: , также .

Случай-2: .

1). Отмечаем: очевидных решений исходного уравнения нет. Учитывая , заданное уравнение представим в виде: == и применим стандартный алгоритм решения уравнения.

2). Примем и запишем: =. Из условия: получаем решение: . Учитывая , получаем частные решения заданного уравнения в виде: – две прямые, проходящие через начало координат .

3). Принимая , запишем: – общее решение уравнения. В нашем случае: , или: , где . Из соображений удобства, можно записать общее решение в виде:

Ответ: общее решение уравнения: , также .

Замечание: Многие Случай-2 не выделяют (не замечают, в шахматах это называют – зевок).

☻

Задача-2, вариант:.

Требуется решить однородное уравнение, заданное в виде: , где функции и– однородные одного порядка–исходнаязапись. От этой записи нетрудно перейти к уравнению:==–стандартнаязапись однородного уравнения. Далее, используя результат Задачи-2 для варианта:, следует применитьстандартный алгоритмрешения однородного уравнения:.

Замечание: При переходе от исходной записи уравнения к записи в форме: требуется проверка условий =0 и =0 с целью выделения возможных решений из исходной записи уравнения: – прямая, параллельная оси и – прямая, параллельная оси .

☺☺

Пример 2–09: Решить дифференциальное уравнение: .

Решение:

1). Отмечаем: = и =. Очевидные решения исходного уравнения нетрудно заметить: – ось и – ось .

2). Перепишем исходное уравнение: == 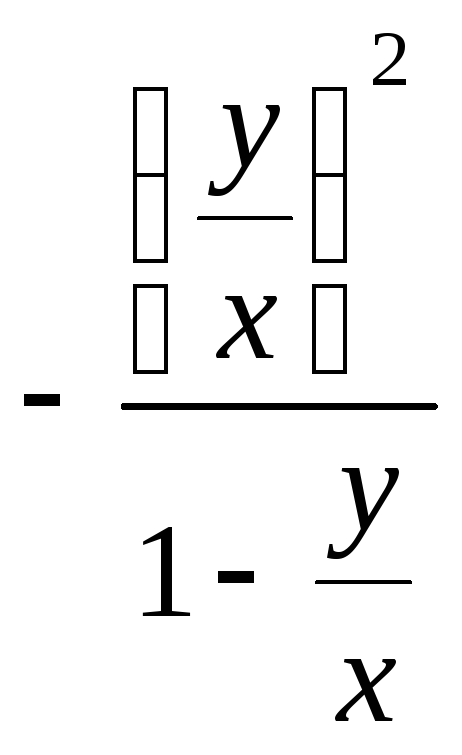и применим стандартный алгоритм решения уравнения.

3). Примем и запишем: ==. Из условия: получаем решение: . Учитывая , получаем частное решение , которое уже учтено.

4). Принимая , запишем: – общее решение уравнения. В нашем случае: , или , или , где .

Ответ: общее решение уравнения: , также и .

Пример 2–10: Решить дифференциальное уравнение: .

Решение:

Случай-1.

1). Отмечаем: = и =. Очевидные решения исходного уравнения нетрудно заметить: – ось .

2). Перепишем исходное уравнение в виде ==, учтено: , . Далее применяем стандартный алгоритм решения однородного уравнения.

3). Примем и запишем: =. Так как принято , равенство: невозможно.

4). Учитывая , запишем: – общее решение уравнения. В нашем случае: =. Учитывая опыт интегрирования рациональных выражений, сразу заметим, что вычисление интеграла: потребует значительных усилий!

Случай-2.

2). Перепишем исходное уравнение в виде ==, учтено: , . Далее применяем стандартный алгоритм решения однородного уравнения.

3). Примем и запишем: =. Используя равенство: , получаем частные решения: . Учитывая , получаем частные решения заданного уравнения в виде: – две прямые, проходящие через начало координат ..

4). Учитывая , запишем: – общее решение уравнения. В нашем случае: =, или , или . Учитывая: , можем записать окончательно: – общее решение уравнения. Учитывая теорию кривых линий 2-го порядка (аналитическая геометрия), отмечаем: семейство интегральных кривых дифференциального уравнения есть множество гипербол: .

Ответ: общее решение уравнения: , также .

Замечание: Даже из нескольких Примеров нетрудно заметить, что решение дифференциальных уравнений требует достаточно высокой математической культуры: здесь и элементарная алгебра, и аналитическая геометрия, и много из математического анализа!..

☻