12.2. Собственные векторы и собственные значения линейного оператора

Определение 4. Квадратные матрицы иназываются подобными, если существует невырожденная матрица , такая, что

.

Теорема 2. Пусть - линейное пространство, (I) и (II) - два базиса в , - матрица перехода от(I) к (II), - линейный оператор в, - матрица операторав(I), - матрица операторав(II). Тогда

.

Это утверждение примем без доказательства.

Пусть . Матрица, где- единичная матрица порядка, а- произвольное вещественное число, называетсяхарактеристической матрицей для . Она имеет вид

.

Определитель - некоторый многочлен порядкаотносительно.

Определение 5. Многочлен называется характеристическим многочленом матрицы, а его корни - характеристическими корнями матрицы .

Теорема 3. Подобные матрицы имеют одинаковый набор характеристических корней.

Доказательство. Пусть ,- невырожденная матрица. Имеем

.

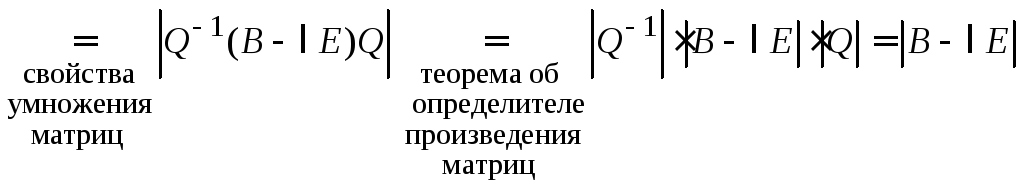Характеристические многочлены матриц В и С совпадают, следовательно, совпадают и характеристические корни.

Теорема доказана.

Следствие. Матрицы, задающие линейный оператор в различных базисах, имеют один набор характеристических корней (теорема 2 + теорема 3).

Определение 6. Характеристические корни матрицы линейного оператора (в любом базисе) называются характеристическими корнями линейного оператора.

Определение 7. Весь набор характеристических корней называется спектром оператора.

Определение 8. Пусть - линейное пространство, - линейный оператор в. Векторназывается собственным вектором оператора, если найдется действительное числотакое, что

.

Число называется собственным значением, соответствующим данному собственному вектору.

Справедливо следующее утверждение, которое приведем без доказательства.

Теорема 4. Действительные характеристические корни линейного оператора, если они существуют, и только они, служат собственными значениями линейного оператора.

Пример 5. Найти собственные векторы и собственные значения линейного оператора зеркального отражения относительно оси .

Решение. Матрица оператора была найдена в примере 2: .

Составим характеристическое уравнение:

,

откуда и,.

Числа ,- характеристические корни линейного оператора (в соответствии с определением 6), они действительны и, согласно теореме 4, являются собственными значениями. Найдем соответствующие им собственные векторы.

По определению собственного вектора , но, следовательно, ищем векторы, удовлетворяющие уравнению, или, или

. (12.3)

При имеем. Подставим ее в (12.3):

,

что равносильно системе уравнений

(12.4)

откуда , и решением системы (12.4) являются все векторы вида

,

- произвольное вещественное число, отличное от нуля.

При получаем, подставляем в (12.3):

,

получаем систему уравнений

откуда ,- произвольное вещественное число, отличное от нуля.

Геометрически это означает, что любой ненулевой вектор, приложенный к началу координат с концом на оси, является собственным, отвечающим собственному значению(действие на него операторасводится к умножению его на, а любой ненулевой вектор с концом на осиявляется собственным, отвечающим собственному значению(т.е. действие операторана этот вектор заключается в умножении его на(рис. 12.5)).

Упражнение. - линейное пространство всех геометрических векторов, - линейный оператор проектирования на ось. Найти все его собственные числа и собственные векторы.