Лекция 13 Евклидовы пространства

Определение евклидова пространства. Ортогональные и ортонормированные базисы. Процесс ортогонализации Шмидта

13.1. Понятие евклидова пространства

Определение 1. Евклидовым пространством называется n-мерное линейное пространство, в котором каждой паре векторов поставлено в соответствие вещественное число, называемое скалярным произведением векторов и (это число обозначим ), причем выполняются следующие аксиомы:

1. ;

2. ;

3. ;

4. .

Замечание. Аксиомы 2 и 3 справедливы также в форме 2’: и форме 3’: .

Пример 1. Пусть - линейное пространство геометрических векторов, скалярное произведение определено равенством

. (13.1)

Аксиомы 1 - 4 выполняются (см. алгебраические свойства скалярного произведения, доказанные в Лекции 2), следовательно, со скалярным произведением, определенным равенством (13.1), является евклидовым пространством.

Пример 2. В линейном пространстве арифметических векторов формула

, (13.2)

где , , задает скалярное произведение. Докажем это. Проверим выполнение аксиом 1 - 4. Поскольку компоненты - вещественные числа, имеем

следовательно, аксиома I выполняется.

Пусть . По определению сложения в . Имеем

,

аксиома 2 справедлива.

Пусть - произвольное вещественное число. По определению умножения вектора на число в

.

Далее имеем

,

аксиома 3 выполняется.

Проверим выполнение аксиомы 4:

Если , то среди компонент вектора найдется , , тогда и , следовательно, аксиома 4 выполняется.

Таким образом, линейное пространство арифметических векторов со скалярным произведением (13.2) является евклидовым пространством.

В любом евклидовом пространстве справедливы следствия из аксиом 1 - 4:

а) ;

б) если , , то

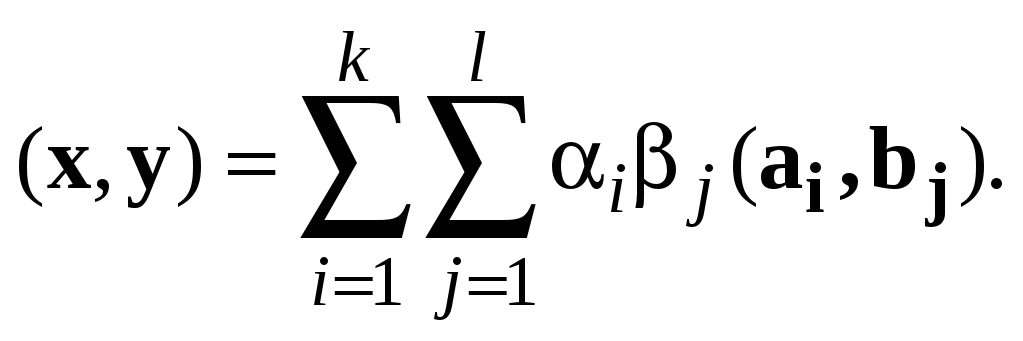
Доказательство следствий проведите самостоятельно.

Определение 2. Нормой вектора называется число, равное .

Обозначим норму . Норма - аналог длины вектора, определенной для геометрических векторов.

Угол между векторами и в евклидовом пространстве определяется равенством

. (13.3)

Покажем, что угол действительно можно определить равенством (13.3), т.е. покажем, что

.

Теорема 1 (неравенство Коши - Буняковского). Для любого и любого справедливо неравенство

. (13.4)

Доказательство. Пусть - произвольное вещественное число. Положим . Тогда по аксиоме 4 имеем

.

Воспользуемся аксиомами 1 - 3:

.

Так как , то дискриминант квадратного трехчлена неположителен:

.

Отсюда или , и неравенство (13.4) выполняется.

Теорема доказана.

Упражнения.

1. Пусть и - произвольные векторы пространства арифметических векторов . Показать, что скалярное произведение в можно определить следующими способами:

а) ; б) .

Вычислить скалярное произведение векторов и каждым из указанных способов.

2. Доказать, что в пространстве соотношение

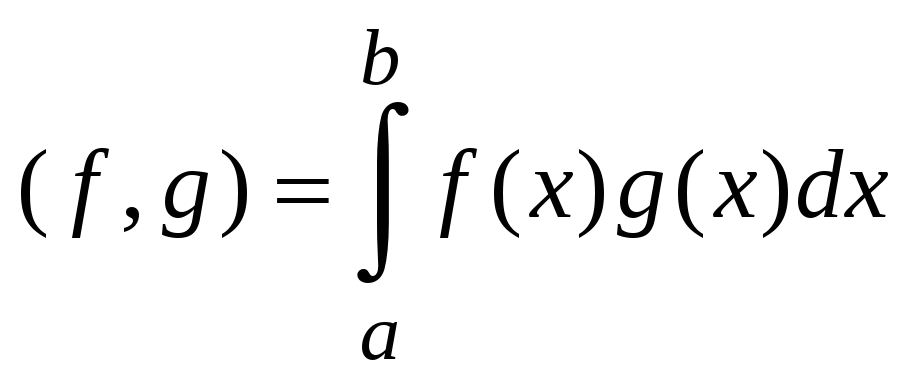
задает скалярное произведение. Написать неравенство Коши - Буняковского для этого пространства.