
13.3. Линейные операторы в евклидовом пространстве
Определение
7.
Квадратная
матрица
![]() называется ортогональной, если
называется ортогональной, если
![]() .
.
Пример
5.
В линейном пространстве
![]() всех геометрических векторов плоскости
матрица линейного оператора поворота
на угол
всех геометрических векторов плоскости
матрица линейного оператора поворота
на угол
![]() против часовой стрелки имеет вид
против часовой стрелки имеет вид
![]() .
.
Для
нее
![]() ,
и, следовательно,
,
и, следовательно,
![]() - ортогональная
матрица.
- ортогональная
матрица.
Отметим некоторые свойства ортогональной матрицы.
Утверждение
1.
Квадратная матрица
![]() является ортогональной тогда и только
тогда, когда ее столбцы составляют
ортонормированную систему арифметических
векторов.
является ортогональной тогда и только
тогда, когда ее столбцы составляют
ортонормированную систему арифметических
векторов.
Доказательство.
Необходимость.
Пусть
![]() ,
,
![]() ,
,
![]() ортогональна.
ортогональна.
Имеем
 ,
,
 .
.
В
соответствии с правилом умножения
матриц
![]() ,
,
![]() ,
где
,
где
![]() .
(13.8)
.
(13.8)
Так
как
![]() ортогональна, то
ортогональна, то
![]() ,
и, следовательно,
,
и, следовательно,
![]() (13.9)
(13.9)
Равенства
(13.8) и (13.9) означают, что строки матрицы
![]() ,
рассматриваемые как арифметические
n-мерные
векторы, составляют ортонормированную
систему, необходимость тем самым
доказана.
,
рассматриваемые как арифметические
n-мерные
векторы, составляют ортонормированную
систему, необходимость тем самым
доказана.
Достаточность.
Пусть
строки матрицы
![]() составляют ортонормированную систему
арифметических векторов. Тогда в
соответствии с введенными выше
обозначениями (см. (13.8))
составляют ортонормированную систему
арифметических векторов. Тогда в
соответствии с введенными выше
обозначениями (см. (13.8))
![]()
Но
это означает, что
![]() и, следовательно,
и, следовательно,
![]() (в силу единственности обратной матрицы)
и
(в силу единственности обратной матрицы)
и
![]() ортогональна.
ортогональна.
Утверждение 2. Матрица перехода от ортонормированного базиса евклидова пространства к любому другому его ортонормированному базису является ортогональной.
Доказательство.
Пусть
![]() (I)
и
(I)
и
![]() (II)
– два ортонормированных базиса в
(II)
– два ортонормированных базиса в
![]() .
.
![]() ,
,
![]() ,
- матрица перехода от (I)
к (II).
,
- матрица перехода от (I)
к (II).
В соответствии с определением матрицы перехода от базиса к базису справедливо равенство
 ,
,
или
![]() ,
,
![]() .
(13.10)
.
(13.10)
Так
как (II)
– ортонормированный базис, то
![]()
Используя (13.10), получаем
![]()
а
это означает, что столбцы матрицы
![]() составляют ортонормированную систему.
Привлекая утверждение I,
заключаем, что
составляют ортонормированную систему.
Привлекая утверждение I,
заключаем, что
![]() - ортогональная матрица.
- ортогональная матрица.
Упражнения. Доказать следующие свойства ортогональной матрицы.
1.
Если
![]() - ортогональная матрица, то
- ортогональная матрица, то
![]() .
.
2.
Если
![]() - ортогональная матрица, то
- ортогональная матрица, то
![]() тоже ортогональная.
тоже ортогональная.
3.
Если
![]() - ортогональная матрица, то
- ортогональная матрица, то
![]() тоже ортогональная.
тоже ортогональная.
4.
Матрица
![]() является ортогональной в том и только
в том случае, когда ее строки составляют
ортонормированную систему арифметических
векторов.
является ортогональной в том и только
в том случае, когда ее строки составляют
ортонормированную систему арифметических
векторов.
Определение
8.
Линейный
оператор
![]() в евклидовом пространстве
в евклидовом пространстве
![]() называется ортогональным, если
называется ортогональным, если
![]()
![]()
(оператор сохраняет норму любого вектора).
Пример
6.
Евклидово пространство
![]() - пространство всех геометрических
векторов плоскости, скалярное произведение
введено равенством
- пространство всех геометрических
векторов плоскости, скалярное произведение
введено равенством
![]() ,
,
![]() - оператор поворота на угол
- оператор поворота на угол
![]() против хода часовой стрелки. Оператор
против хода часовой стрелки. Оператор
![]() - ортогональный.
- ортогональный.
В
самом деле, оператор
![]() - линейный, так как из геометрических
соображений ясно, что
- линейный, так как из геометрических
соображений ясно, что
![]() - действительного числа
- действительного числа
![]() ,
,
![]()
![]()
![]() .
А так как при повороте длина любого
вектора сохраняется, то
.
А так как при повороте длина любого
вектора сохраняется, то
![]() - ортогональный оператор.
- ортогональный оператор.
Теорема
4.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() - ортогональный оператор в
- ортогональный оператор в
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
(![]() сохраняет скалярное произведение).
сохраняет скалярное произведение).
Доказательство.
Пусть
![]() ,
,
![]() ,
рассмотрим
,
рассмотрим
![]() .
.
Имеем
![]()
![]()
![]() .
(13.11)
.
(13.11)
С другой стороны,
![]()
![]() .
(13.12)
.
(13.12)
Сравнивая
(13.11) и (13.12) заключаем, что
![]() .
.
Теорема доказана.
Теорема
5.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() (I)
- ортонормированный базис,
(I)
- ортонормированный базис,
![]() - ортогональный оператор в
- ортогональный оператор в
![]() .
Тогда
система
векторов
.
Тогда
система
векторов
![]() (II)
- ортонормированный базис.
(II)
- ортонормированный базис.
Доказательство. Имеем
![]()
и,
следовательно,
![]() - ортонормированная система. Но тогда
- ортонормированная система. Но тогда
![]() ,
и по теореме 2 система (II)
линейно независима, а так как
,
и по теореме 2 система (II)
линейно независима, а так как
![]() ,
(II)
– базис, и по доказанному – ортонормированный.
,
(II)
– базис, и по доказанному – ортонормированный.
Теорема доказана.
Теорема
6.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() - ортогональный оператор в
- ортогональный оператор в
![]() .
Тогда
.
Тогда
![]() в любом ортонормированном базисе
задается ортогональной матрицей.
в любом ортонормированном базисе
задается ортогональной матрицей.
Доказательство.
Пусть
![]() (I)
– произвольный ортонормированный базис
в
(I)
– произвольный ортонормированный базис
в
![]() .
Тогда система векторов
.
Тогда система векторов
![]() (II)
– тоже ортонормированный базис (теорема
5).
(II)
– тоже ортонормированный базис (теорема
5).
Пусть
![]() - матрица оператора
- матрица оператора
![]() в базисе (I).
в базисе (I).
В соответствии с определением матрицы оператора (определение 3 в лекции 12) справедливо следующее равенство:

и,
следовательно, матрица
![]() является матрицей перехода от базиса
(I)
к базису (II)
(см. равенства (11.1) в лекции 11). Тогда в
силу доказанного выше утверждения 2
матрица
является матрицей перехода от базиса
(I)
к базису (II)
(см. равенства (11.1) в лекции 11). Тогда в
силу доказанного выше утверждения 2
матрица
![]() является ортогональной.
является ортогональной.
Теорема доказана.
Определение
9.
Линейный
оператор
![]() в евклидовом пространстве
в евклидовом пространстве
![]() называется самосопряженным (симметрическим),
если
называется самосопряженным (симметрическим),
если
![]()
![]()
![]() .
.
Пример
7.
Пусть
![]() - произвольное евклидово пространство,
- произвольное евклидово пространство,
![]() - тождественный оператор, т.е.
- тождественный оператор, т.е.
![]()
![]() .
.
Имеем
![]()
![]() ,
следовательно,
,
следовательно,
![]() симметрический.
симметрический.
Пример
8.
Пусть
![]() - произвольное евклидово пространство,
- произвольное евклидово пространство,
![]() - некоторое действительное число. Положим
- некоторое действительное число. Положим
![]()
![]() .
.
Справедливо
равенство
![]()
![]() ,
,
и,
следовательно,
![]() - симметрический.
- симметрический.
Отметим некоторые свойства симметрического оператора.
Определение
10.
Матрица
![]() ,
,
![]() ,
называется симметрической, если
,
называется симметрической, если
![]()
![]() .
.
Теорема
7.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() (I)
- ортонормированный базис в
(I)
- ортонормированный базис в
![]() ,
,
![]() - симметрический оператор в
- симметрический оператор в
![]() .
Тогда
матрица
оператора
.
Тогда
матрица
оператора
![]() в (I)
симметрическая.
в (I)
симметрическая.
Доказательство.
Пусть
![]() ,
,
![]() - матрица оператора
- матрица оператора
![]() в (I).
В соответствии с определением матрицы
оператора справедливы следующие
равенства:
в (I).
В соответствии с определением матрицы
оператора справедливы следующие
равенства:
![]() ,
,
![]() ,
,
…………………………………….. ... (13.13)
![]() .
.
Воспользовавшись соотношениями (13.13), получим
 .
(13.14)
.
(13.14)
 .
(13.15)
.
(13.15)
Так
как
![]() - симметрический оператор,
- симметрический оператор,
![]() .
.
Сравнивая
(13.14) и (13.15), находим, что
![]() ,
и
матрица
,
и
матрица
![]() - симметрическая.
- симметрическая.
Теорема доказана.
Теорема
8.
Если
линейный оператор
![]() ,
определенный в евклидовом пространстве
,
определенный в евклидовом пространстве
![]() ,
задается хотя бы в одном ортонормированном
базисе симметрической матрицей, оператор
,
задается хотя бы в одном ортонормированном
базисе симметрической матрицей, оператор
![]() - симметрический.
- симметрический.
Доказательство.
Пусть
![]() - линейный оператор в евклидовом
пространстве
- линейный оператор в евклидовом
пространстве
![]() ,
,
![]() (I)
– произвольный ортонормированный базис
в
(I)
– произвольный ортонормированный базис
в
![]() ,
,
![]() ,
,
![]() - матрица оператора
- матрица оператора
![]() в базисе (I)
(т.е. справедливы равенства (13.13)),
в базисе (I)
(т.е. справедливы равенства (13.13)),
![]() - симметрическая, или
- симметрическая, или
![]()
![]() .
.
Пусть
![]() ,
,
![]() .
Так как (I)
– базис, найдутся числа
.
Так как (I)
– базис, найдутся числа
![]() и
и
![]() такие, что
такие, что
![]() ,
,
![]() .
.
Имеем

 ,
(13.16)
,
(13.16)
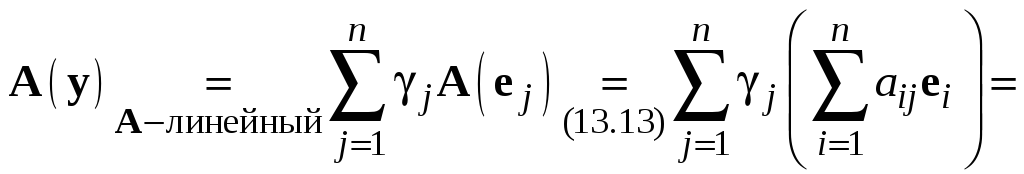
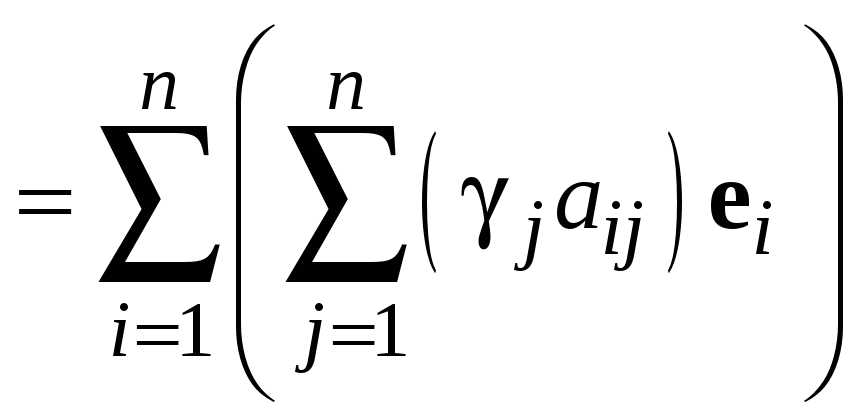 .
(13.17)
.
(13.17)
Используя равенства (13.16) и (13.17) и условие, что (I) – ортонормированный базис, получим
 ,
,
 .
.
Так
как
![]() симметрическая,
симметрическая,
![]() и
и
![]() ,
а это означает, что оператор
,
а это означает, что оператор
![]() симметрический.
симметрический.
Теорема доказана.
Приведем без доказательства еще одно свойство самосопряженного оператора.
Теорема
9.
Пусть
![]() - евклидово пространство,
- евклидово пространство,
![]() - линейный оператор в
- линейный оператор в
![]() .
Оператор
.
Оператор
![]() является симметрическим тогда и только
тогда, когда в
является симметрическим тогда и только
тогда, когда в
![]() существует ортонормированный базис,
составленный из собственных векторов
оператора
существует ортонормированный базис,
составленный из собственных векторов
оператора
![]() .
.
Пример
9.
Линейный оператор
![]() ,
определенный в евклидовом пространстве
,
определенный в евклидовом пространстве
![]() ,
задан в некотором ортонормированном
базисе матрицей
,
задан в некотором ортонормированном
базисе матрицей
![]() .
Выяснить,
существует ли для этого оператора базис,
в котором его матрица диагональна.
.
Выяснить,
существует ли для этого оператора базис,
в котором его матрица диагональна.
Так
как
![]() - симметрическая матрица (в ортонормированном
базисе), оператор
- симметрическая матрица (в ортонормированном
базисе), оператор
![]() симметрический (теорема 8), а тогда по
теореме 9 для него существует базис,
состоящий из собственных векторов. В
этом базисе матрица оператора диагональна
(лекция 12, § 12.3).
симметрический (теорема 8), а тогда по
теореме 9 для него существует базис,
состоящий из собственных векторов. В
этом базисе матрица оператора диагональна
(лекция 12, § 12.3).
