10

1.3. Дифференциальные уравнения с разделенными и разделяющимися переменными

Дифференциальное уравнение с разделенными переменными имеет

вид

В уравнении с разделенными переменными перед дифференциалом dx стоит функция только одной переменной x, а перед дифференциалом dy стоит функция переменной y. Такие уравнения можно почленно интегрировать. В результате получим

∫M (x)dx + ∫N(y)dy = C

или

где

F(x) = ∫M (x)dx, Ф(y) = ∫N(y)dy .

Конечное (не дифференциальное) соотношение (1.8) и является общим интегралом уравнения (1.7).

Пример. Решить уравнение ex dx + ln ydy = 0.

Очевидно, это уравнение с разделенными переменными. Интегрируя его, получим

∫ex dx + ∫ln ydy =C.

Следовательно, общий интеграл уравнения будет

ex + y(ln y −1) = C.

Дифференциальное уравнение вида

в котором коэффициенты при дифференциалах распадаются на множители, каждый из которых зависит только от одной переменной, называется диффе-

ренциальным уравнением с разделяющимися переменными. Уравнение

(1.9) делением обеих частей на произведение функций N1(y)M 2 (x) ≠ 0 приводится к уравнению с разделенными переменными

Пример. Решить равнение (1+ y2 )xdx + (1+ x2 ) ydy = 0 . Разделяем переменные делением на выражение (1+ y2 )(1+ x2 ) ≠ 0 :

1+xx2 dx +1+yy2 dy = 0.

Интегрируем полученное уравнение с разделенными переменными

∫1+xx2 dx + ∫1+yy2 dy = C1.

Тогда

12 ln(1+ x2 )+ 12 ln(1+ y2 ) = C1

Так как C1 - произвольная постоянная, принимая ее для упрощения полученного выражения в виде

C1 = 12 lnC,

представим общий интеграл уравнения в виде (1+ x2 )(1+ y2 ) = C.

1.4. Однородные дифференциальные уравнения

Если уравнение y′ = f (x, y) или M (x, y)dx + N (x, y)dy = 0 не меняется при замене x на kx, а y на ky, то оно называется однородным.

Однородное дифференциальное уравнение подстановкой t = xy

приводится к уравнению с разделенными переменными. Пример. Решить уравнение

(x + y)dx + (y − x)dy = 0.

Интегрируя его, находим

arctg t − 12 ln (1+t 2 ) = lnx +C

или

arctg t −ln(x 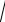1+t 2 ) = C.

Возвращаясь к старой переменной, получим общий интеграл исходного уравнения в виде

C = arctg xy − ln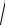x2 + y2 .

1.5. Дифференциальные уравнения, приводящиеся к однородным

Дифференциальное уравнение вида

13

a1α +b1β + c1 = 0,a2α +b2 β + c2 = 0.

Действительно, учитывая, что du = dx, dv = dy, следовательно, dydx = dudv , и

подставляя (1.11) в (1.10), получим однородное уравнение относительно новой функции v(u).

Полагая далее

t = uv ,

приводим последнее уравнение к уравнению с разделяющимися переменными.

2) Если определитель

то уравнение (1.10) сразу приводится к уравнению с разделенными переменными заменой