Обработка результатов моделирования

Д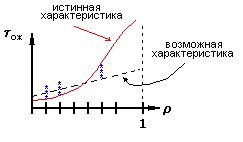ля получения зависимости:  _ож = ( ), где : - коэффициент загрузки системы;  _ож - время ожидания; .

Т.к. моделирование стохастическое, то возможно получить несколько значений для заданного . По полученным значениям, путем решения задач математической статистики (сглаживание кривой), используются правила статистической проверки гипотезы.

Постановка задачи :

1. Получить экспериментальную зависимость одной величины “y” , от другой “x”; y=(x) .

2. Определить изменение параметра независимой переменной “x” . И для них производится ряд экспериментов. ( Это число зависит от точности полученных результатов () , вероятность того, что результаты будут лежать в данном интервале ).

3. Получение результатов.

4. Определение средних значений результатов.

5. Проведение линии через точки средних значений . ( Линия может проходить и не через среднее значение , а находиться в заданном вероятностном интервале ). Линия регрессии - линия построения по выше описанным правилам. Уравнение регрессии - уравнение , описывающее построенную линию. Решается методом наименьших квадратов.

6. Определение коэффициентов для получения уравнений. Для этого необходимо взять две точки ( для линейной системы ) и составить уравнение : y₁ = kx₁ + b ; y₂ = kx₂ + b .

7. Проверка адекватности модели. Используют статистические вероятностные критерии ( Стьюдента - для отдельных величин , Пирсона , Колмогорова , Фишера ) . Адекватность - данное уравнение регрессии , отвечающее полученным результатам .

Метод планирования эксперимента

Цель метода : Обеспечение наивысшей точности при минимальных затратах на проведение эксперимента.

Позволяет планировать эксперимент так , чтобы сразу получить зависимость :

y =  ( x₁ , x₂ , … ) . Предполагаем , что y =  ( x ) - непрерывна и дифференцируема , тогда мы можем разложить ее в ряд Тейлора :

Для двух переменных :

Е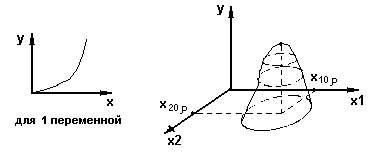сли спроецировать линии одинаковых значений на плоскость , то получим :

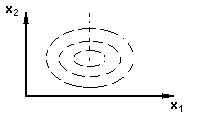
Факторы эксперимента - независимые переменные ( х₁ , х₂ ) .

Отклик ( функция отклика ) - зависимыя переменная ( у ) .

Факторное пространство ( фазовое ) - пространство , в котором определена “у” . В таком случае x_i – фазовые координаты.

Критерий эффективности - задача поиска минимального и максимального значения функции ( т.к. она не линейная ).

Исследование на всем фазовом пространстве не производится , а выделяется область , где

( х₁ , х₂ ) - оптимальные значения , т.е. где у - достигает своего максимума. В поцессе статистических испытаний имитационной модели решаются две задачи :

1. Нахождение области оптимальных значений ( х_{1 оп} , х_{2 оп} ) ;

2. Получение математического описания в виде зависимости функции отклика “у” от факторов х₁ , х₂ , и т.д.

Нахождение области оптимальных значений

Особенности :

• функциональная связь между параметрами неизвестна.

• методы оптимизации не работают => оптимизация осуществляется в процессе эксперимента .

Стандартные методы оптимизации :

• y^ - экстремум ;

• y^ - max и min.

Для оптимизации принимают градиентные методы :

1. Метод Гаусса ( наиболее известный ).

а) Пусть существует исходная точка

б)

2. Метод Гаусса –.Зеймана ).

Фиксированные значения х₂ перемещаются по х₁ до достижения максимального значения , потом фиксируется х₁ ( найденное ) и перемещается по х₂ .

3. Симплексный метод.

Симплекс - в n - мерном пространстве правильный многоугольник , в 2 – мерном : правильный треугольник.

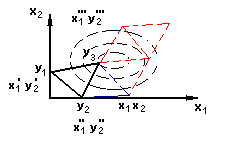
• Пусть существует точка

• Строим правильный треугольник

• Координаты вершин задаются эксперементатором ( произвольно )

• Измеряется функция отклика в этих вуршинах и получаются значенияя : у₁ , у₂ , у₃ . Тогда ( см. рис. ) у₃ > у₁ + у₂ , у₂ > у₁ ( т.к. ближе к линии ) => у₁ минимальное значение функции.

• Производится отражение относительно грани для вершины у₁^ определяются новые значения х₁^ , х₂^ и для них вычисляется функция отклика.

• Наименьшее значение функции отклика ( см. пример ) будет соответствовать вершине у₂.

• Далее производится отражение относительно линии у₃ у₁^ и т.д. до тех пор , пока значение функции отклика во всех вершинах не будут одинаковы ( в пределах погрешности опыта ).

С помощью любого из рассмотренных методов можно приблизиться к области оптимальных значений.

Этот метод используется для решения систем линейных уравнений и для решения задач линейного программирования.

П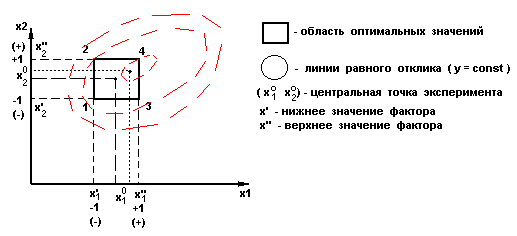олучение математического описания функции отклика от факторов

В области экстремума эта зависимость бывает 1 – го или максимум 2 – го порядка , линейной или квадратичной.

Пусть существует область оптимальных значений , полученных симплексным методом. Получим математическое описание для данной области.

Цель эксперимента : получить зависимость - для n –го параметра ; в случае двух параметров – уравнение регрессии :

Если вид ( порядок ) уравнения регрессии определен , то задача сводится к определению коэффециента регрессии : b₀ , b_{1 ,} b₂ и т.д.

В области оптимальных значений ( область экстремума ) линии менне искривлены , т.е. влияние квадратичных членов уравнения не учитываются . Чем меньше область , тем больше вероятность того , что уравнениерегрессии будет иметь вид :

Значение b_i получат :

1. x и х - задаются эксперементально. ( х₀ х₀ ) - цетнр эксперимента , задается экспериментатором по отношению к области оптимальных значений .

2. Задаются границы интервала варьирования.

3. Производится кодирование переменных :

x  -1 ( - )

х  +1 ( + )

4. Составляется матрица планирования эксперимента

х₀ - фиктивная переменная ; ( x₀=b₀ ) = +1 ; x₁ = x ; x₂ = x ; т.е. проводятся измерение в т.1 , т.2 , т.3 , т.4

Такой эксперимент называется Факторным эуспериментом порядка N = 2² , т.е необходимо 4 эксперимента для вычисления коэффициента регрессии .

5. Для нахождения b_{0 :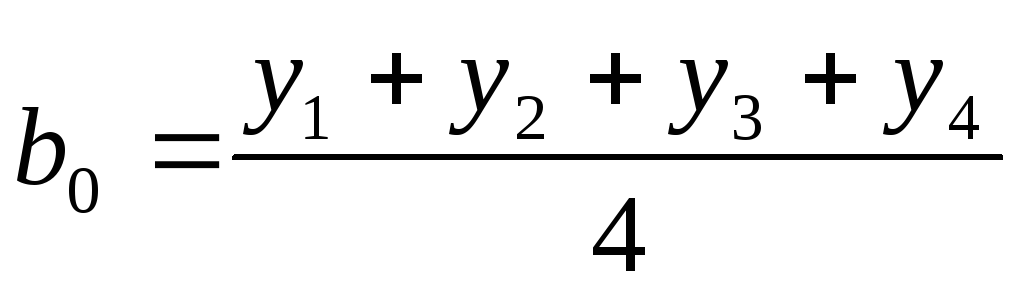} с учетом знака в столбцах х_i . Для нахождения b₁ :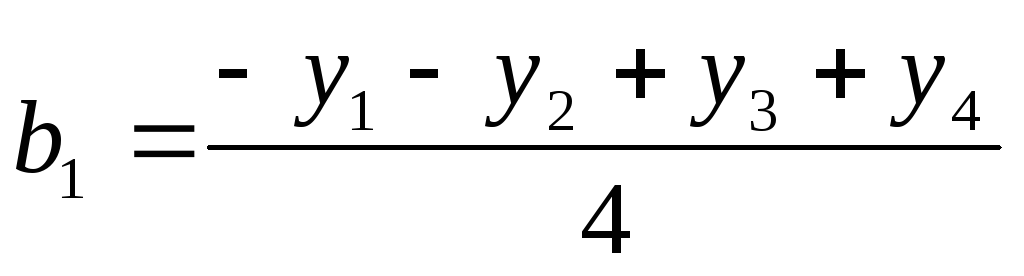и т.д. При таком эксперименте может получиться только коэффициенты : b_{0 ,} b_{1 ,} b_{2 ,} b_{12 .}

6. По результатам эксперимента строится регрессионная модель эксперимента y=(x).

7. Статистический анализ уравнения регрессии :

- Проверка значимости коэффициента регрессии ( статистической зависимости ) . Выдвигается гипотеза статистического равенства , где коэффициент регрессии = 0. Проверяется данная гипотеза с использованием критерия Стьюдента. Если гипотеза принимается , то коэффициент регрессии признается статистически незначимым , и может быть отброшен ( даже если он имеет значение  0 ) , и наоборот , если не подтвердится , то коэффициент значим. При планировании эксперимента полученные оценки коэффициента регрессии является независимым => при отбрасывании пересчет не производится.

- Проверка адекватности полученного уравнения регрессии. Производят с помощью критерия Фишера. Он позволяет сравнить вторые дисперсии: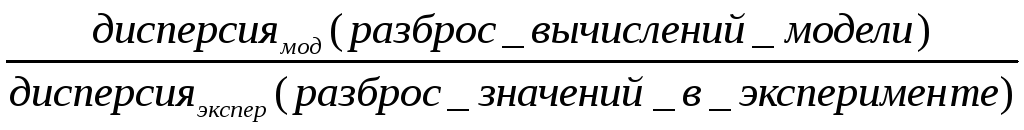. Если_мод=_экспер то уравнение адекватно и наоборот.

Из таблиц Фишера для данного числа измерены и величины переменных ( ? погрешностей ) выбирают число , которое сравнивают с отношением ( если  то принимаем ).