Моделирование случайных ( вероятностных ) объектов.

Эти объекты :

• случайные величины (необходим закон распределения)

• случайные события

• потоки случайных событий

• случайные процессы

Основой для моделирования вероятностных объектов является моделирование случайных чисел равномерно распределенных на интервале ( 0 .. 1).

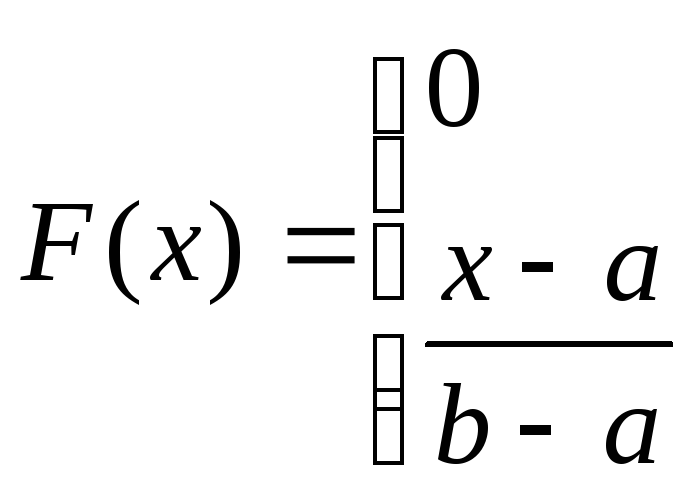
, где F(x) - функция распределения

Если с.в “х” имеет функцию распределения F(x), то распределение с.в равномерно в интервале ( 0 ..1 ).

Существует два требования к датчикам случайных чисел :

1. Требование к длительности периода

Период должен соответствовать тому числу испытаний, которое необходимо.

2. Качество случайных чисел

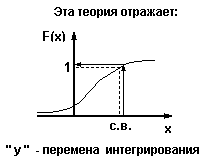
Если эти требования выполняются, то распределение:

х  F(x) с.в. U = F(x) - равномерное в интервале ( 0..1 )

Мы знаем, что функция распределения выражается через плотность распределения:

()

Формирование с.в. с экспоненциальным законом распределения.( частный случай решения ().

- функция распределения для экспоненциального закона.

- плотность распределения

- ()

, тогда выражая “ x “, получим

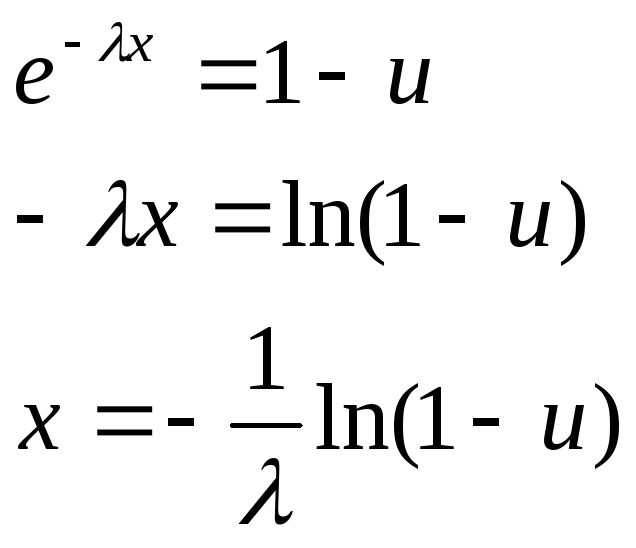
Если U - с.в. распределена в интервале ( 0..1 ), то с.в. ( 1 – U ) будет распределена в интервале ( 0..1 ) равномерно =>

Формула формирования с.в. с экспоненциальным законом в интервале ( 0..1 )

В распределении Пуассона используется та же формула, но с определенным ограничением.

В распределении Эрланга второго потока: сумма двух с.в.

В распределении Эрланга третьего потока: сумма трех с.в.

Формирование случайных событий

Пусть некоторое событие A может наступить с вероятностью P; - противоположное событие, его вероятность:( 1 – Р ) .

Будем формироватьс.в. U, распределенную в интервале ( 0..1 ) .

n₁ + n₂ = N - общее число экспериментов.

N₁ – число экспериментов, попавшее в интервал ( 0..Р )

n₂ – число экспериментов, попавшее в интервал ( Р..1 )

- оценки вероятностей

Т.е при N ибудут совпадать сp и q.

Теперь пусть U – формируется однократно, тогда если:

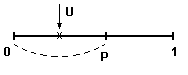U ( 0..P ) => Наступило событие А

U ( P..1 ) => Наступило событие

Схема алгоритма для определения того: свободен ли прибор или занят:

1. Формируем с.в. “ U “ равномерно распределенной на ( 0..1 )

2. Сравниваем “ U “ с “ P “ - вероятности занятости.

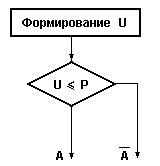
Формирование события из полной группы событий

Полная группа: в результате испытаний обязательно реализуется одно из событий U , где

Р₁ + Р₂ + … Р_n = 1

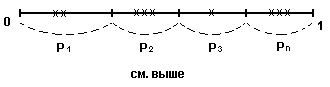
1)

2. Формируем одну с.в. и по попаданию в интервал определяем событие

Формирование потоков случайных событий

Пусть существует поток заявок: Пусть поток – простейший (стационарный Пуассоновский ).

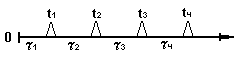
Для формирования потока необходимо сформировать t₁ , t₂ , t₃ - моменты наступления событий, т.е. поступления заявок ,где :

В простейшем потоке  - подчиняется экспоненциальному закону распределения ( формирование с.в. с экспоненциальным законом см. выше ).

Т.е. формирование потока случайных событий сводится по существу к формированию с.в. (  ) с заданным законом распределения.