Московский Государственный Институт Электроники и Математики ( ТУ )

I never saw a wild thing

Sorry for itself

A small bird will drop frozen dead from a bough

Without ever having felt sorry for itself

D.H.Lowrence

Кафедра ВСиС

Теоретические основы проектирования вс

Семестр 1,2

Набор: Преподаватель:

Студент гр.С-91 Жданов В.С.

Степанов а.В.

_________________

Москва 1998 г.

Система состоит из элементов, которые образуют подсистемы.

Элемент – неделимая часть.

Элементы соединяются между собой связями.

Структура системы = элементы + связи между ними.

Для системы необходима цель системы.

Система реализует функцию, определяющую функционирование системы.

Качество системы показывает, насколько удовлетворительно функционирует система, для достижения цели.

Эффективность выражается через критерии и показатели эффективности.

Оптимальная система – это система, лучшая по какому-либо свойству.

Если при проектировании используются несколько критериев, то применяют об’единение критериев путем свертывания.

Методы свертывания

• Выделяют главные критерии, а не главные ограничиваются соответствующими параметрами ( линейное программирование ) – аддитивный показатель.

• Нормирование каждого критерия по отношению к min или max , получая при этом безразмерную величину. Каждой такой величине присваивается свой весовой коэффициент (важность показателя). Для получения общего показателя эффективности производят перемножение веса на относительную величину и складывают.

• Оптимизация по Парето. Сначала производится оптимизация по одному показателю, потом по другому и т.д. Далее выбирается лучший.

Основные показатели В.С.

• Время реакции системы – время от начала ввода заявки (момента образования) до момента ответа системы.

• Время ожидания - время от начала ввода заявки (момента образования) до

• момента начала обработки.

• Вероятность отказа в обслуживании.

• Модель – физическая или абстрактная система адекватно представляющая собой объект исследования.

• Физическая модель – объект в уменьшенных размерах.

• Математическая модель - аналитические (системы массового обслуживания, сети Петри ) и алгоритмические ( концептуальные ).

Свойства модели

• Должна быть адекватной.

• Простой.

- Обеспечивать требуемую точность.

• Результаты, полученные при исследовании модели, должны быть переносимы на сам объект.

Моделирование = построение модели + исследование модели.

Системы массового обслуживания

Есть очередь заявок, обслуживающих приборы.

:

ОП

Если есть очередь и место в ней, то заявка встает в очередь. Выходной поток состоит из обслуженных заявок.

Если система детерминирована по времени, то некоторые заявки могут попасть в выходной поток не обслуженными.

Входящий поток ( поток заявок )

Поток заявок – последовательность моментов поступления сообщений.

T₁ t₂ t₃ t₄ . . . t _n t _n+1

1 – e^{- t} A (t)

A (t) – функция распределения интервалов сигналов между двумя сообщениями.

Интервал [ t _n+1 + t _n ] можно задавать при помощи A (t) .

Интенсивность потока - Если  = dA (t) - средняя длина ( первый момент ) интервала между поступающими сообщениями, тогда -интенсивность - среднее количество сообщений , поступающих в единицу времени. Наиболее распространенный поток имеет функцию распределения ( экспоненциальную ) : А (t) = 1 – e ^{- t} , тогда такой поток называется пуассоновский поток. В систему поступает простейший поток распределения - ЭКСПОНЕНЦИАЛЬНЫЙ.

Пуассоновский поток описывается:

Количество сообщений - вероятность того , что поступит ровно n – сообщений.

P_n(t) = (t)ⁿ e ^-t , где

n 

t  0 ;

 - интенсивность потока заявок.

K – среднее количество заявок за интервал t .

k =  / t

Свойства потока :

1. Стационарность - устойчивость поступления заявок.

Независимо от момента времени функция - постоянна.

2. Ординарность - в любой момент времени приходит только одна заявка. Вероятность того, что за t0 ( малый отрезок времени ) придет несколько сообщений, равных 0 .

3. Отсутствие последствий - системе безразлично сколько заявок пришло до текущей заявки и сколько после, т.е поступающие заявки не зависят от уже поступивших , а зависят только от состояния системы.

Среднее число событий ( заявок ) :

m_x = e ^t = e ^t = t e ^t =

= + e ^t = t e ^t e ^t =  t

Случайная величина – величина , которая в случае опыта со случайным исходом принимает то или иное значение , т.к. таких значений может быть не одно , то все возможные значения случайной величины называются множеством случайных значений.

Случайная величина характеризуется функцией распределения с.в.

F(x) - вероятность того , что с.в примет значение  чем Х.

F(x) = P { X  x }

F( x₂ )  F( x₁)

x ₂  x₁

Случайная величина может быть непрерывной или дисперсной.

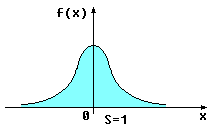(x) = F (x) – плотность распределения вероятности

max там , где крутизна = max , т.е в т.( 0,0 ).

- площадь под графиком , гдеу – переменная интегрирования.

Для дискретной с.в вместо плотности распределения используют гистограмму - вероятность того , что с.в попадает в тот или иной интервал.

С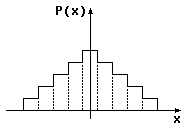уществуют числовые характеристики с.в при помощи которых можно вывестии т.д

m_{x =} x (x) x = X_i P _i - математическое ожидание - среднее значение с.в.

X _i -

P_i - вероятность ее появления.

Дисперсия - отклонение относительно среднего значения с.в.

Среднеквадратичное отклонение

При нормальном распределении ( Гаусса ) все значения с.в сосредоточены в интервале ( - 3 , + 3 ).

Пуассоновский поток

Простейшим видом является стационарный пуассоновский поток , если для него выполняются все три свойства ( см. выше ).

Вероятность поступления заявок:

, где k – событие , - вероятность поступления того , что на интервале t поступит ровно k заявок.

- среднее число заявок , поступившее в простейший поток за время t ( интенсивность поступления заявок ).

Функция распределения - промежуток времени в простейшем потоке между соседними заявками.

Среднее число заявок :

Дисперсия среднего числа заявок:

Графическое представление средней величины заявок ( при t = const и =var )

Плотность распределения