Формирование случайных процессов

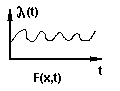
Случайный процесс - если с.в. зависит от времени, то говорят о случайном процессе, как правило с заданной функцией распределения F (x , t )

Бывают :

стационарные – зависят от времени , но F не зависит от времени.

1. Эргодические - позволяют вместо функции распределения оперировать математическим ожиданием и корреляционной функцией. ( когда она затухает -> эргодический процесс ).

2. Нормального распределения.

Произвольный случайный процесс :

- ряд Фурье.

- среднее значение – математическое ожидание случайного процесса.

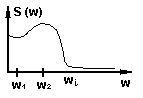
- спектральная плотность ( спектр ) .

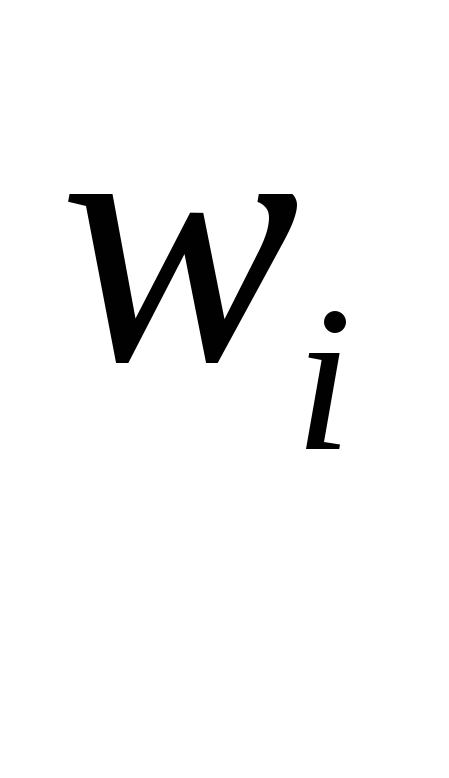- определяется из графика спектральной плотности.

, - некоторые случайные числа , которые выражаются через дисперсию случайного процесса.

Схема реализации случайного процесса:

1. Вычисление среднего значения ( или задаются ).

2. Для выбора w_i задаются функции

3. A_i , B_i – формируют с.в. с заданным законом распределения.

Методы построения имитационных моделей

Основой является: временная диаграмма функционирования системы (см. выше).

1 Метод :

Мы можем просматривать процесс прохождения каждой заявки по системе ( для несложной системы ) .

2 Метод :

Могут быть выделены элементы системы :

• источники заявок , памяти ( модель очереди ) .

• устройства ( модель обслуживаемого устройства )

Эти устройства могут находиться в том или ином состоянии.

Отображение состояний системы и элементов при прохождении заявок :

Существуют подходы :

2.а. Просмотр состояний системы происходит с некоторым дискретным шагом

2.б. Просмотр состояний системы происходит с переменным шагом.

Существуют некоторые моменты времени , когда система меняет свое состояние ( приход , уход заявки , и.т.д. ).Такой процесс называется - событие . По сравнению с 2.а. дает не избыточную информацию , т.е. просматривает состояние системы только после поступления события.

Пример 1 Одноканальная система массового обслуживания с неограниченным ожиданием ( без потерь ) .

Из источника заявок поступает входящий поток . Очередная заявка из потока занимает обслуживающий прибор сразу , если он свободен ; в противном случае заявка встает в очередь. Ограничений на длину очереди и времени ожидания нет.

1. Описание системы ( см. выше ).

2. Построение временной диаграммы .

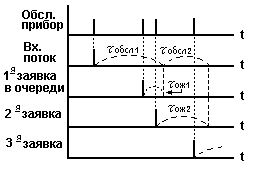
3. Построение имитационного алгоритма.

Формирование вхлдящего потока

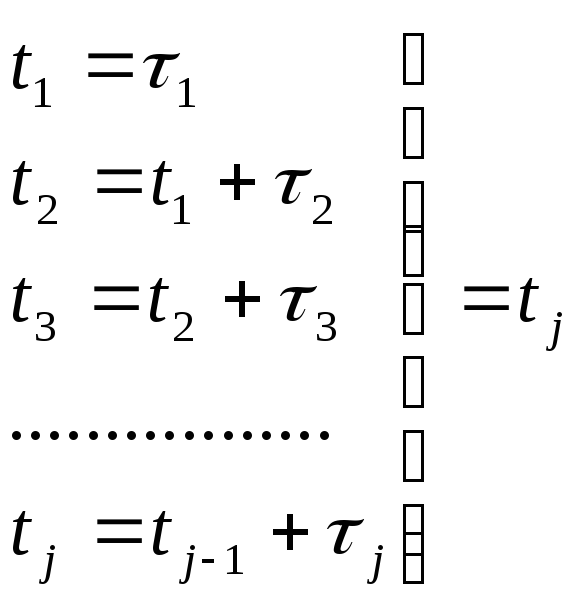- момент поступления очередной заявки. Н.у. : t_j^ok = 0

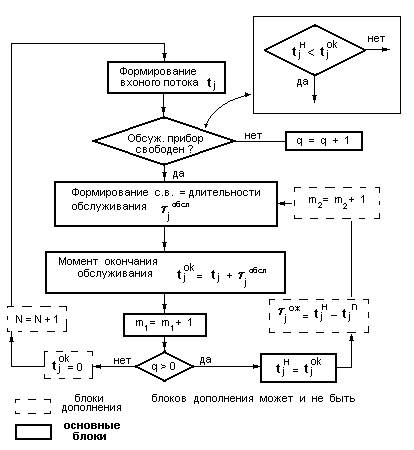
t_{1 -} момент формирования первой заявки

N – число обслужанных заявок ;

q - число заявок в очереди ;

m₁ - число заявок , обслуживаемых без очереди ;

m₂ - число заявок , обслуживаемых по очереди ;

q>0 – определяет , есть ли заявки в очереди ;

t_j + _j - момент окончания обслуживания ;

t_j^н - момент начала обслуживания заявки , выбранной из очереди.

Чтобы определить свободен ли прибор , можно воспользоваться механизмом семафоров , но лучше ( в данном случае ) использовать временное соотношение ( см. диаграмму ).

Если ( t_j^н < t_j^ok ) - то прибор занят , а когда очередь пуста , то необходимо присвоить t_j^ok min значение , например : t_j^ok = 0 .

В результате моделирования необходимо определить показатели эффективности системы :

1. Вероятность обслуживания без ожидания ( Р₀ ) .

2. Вероятность обслуживания с ожиданием ( Р₁ ) .

3. Среднее время ожидания ( ) .

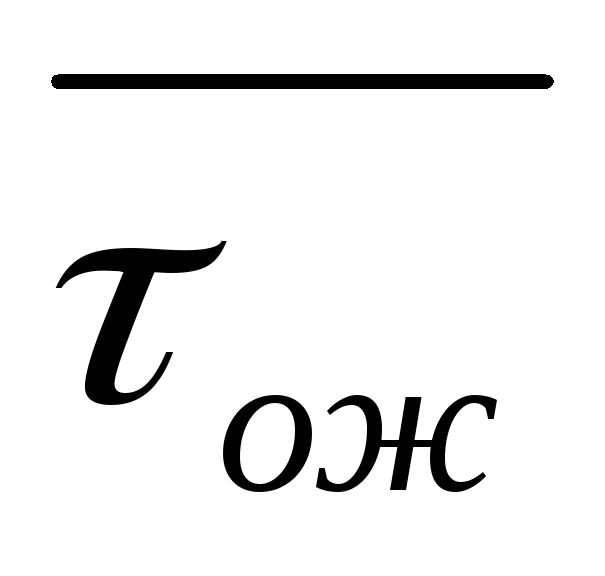4. Загрузка обслуживающего прибора ( среднее относительное время занятости прибора К_з ) . 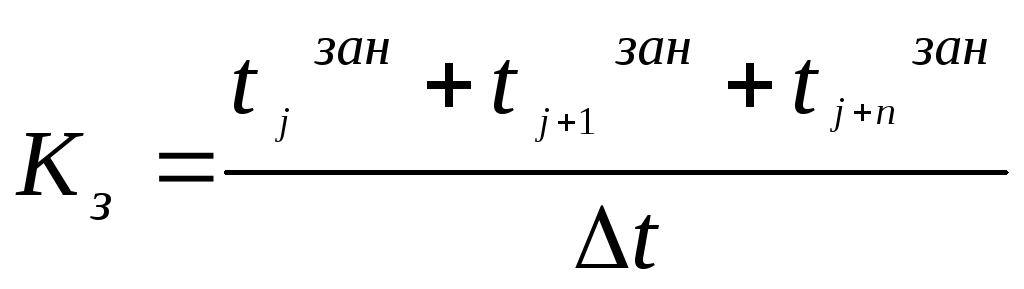, где- длительность интервала

5. Коэффициент простоя обслуживающего прибора ( К_пр ) . К_пр + К_з =1

6. Среднее время ответа ( Т ) 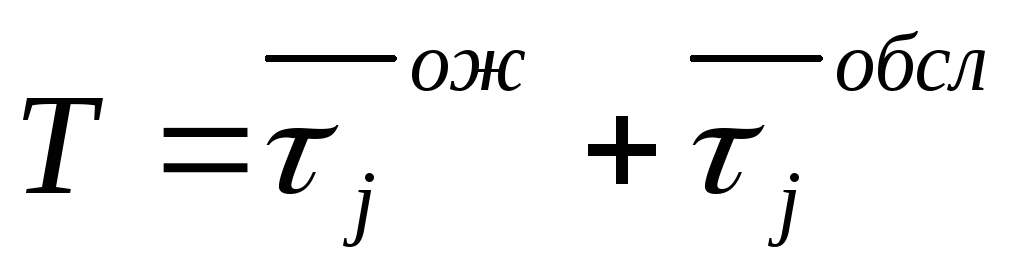( среднее время обслуживания + среднее время ожидания )

7. Общее число заявок

При моделировании системы задают либо число заявок ( N _max ) , либо интервал времени ( T _max ) : ,где t_jⁿ - время поступления заявки , t_j^н – время начала обслуживания.

Особенности : Т.к. время ожидания не ограничено , то очередь будет возрастать , что требует предусмотреть выделение большей памяти.

Пример 2 Многоканальная система массового обслуживания с отказами .

Если обслуживающий прибор свободен , то заявка обслуживается , а если нет , то заявка теряется.

Построение имитационной модели по методу особых состояний

Особые состояния - моменты перехода из одного состояния в другое ( при поступлении очередной заявки , при окончании обслуживания , при потери заявки , при истечени допустимого времени прибываия заявки в системе ).

Для построения имитационной модели в системе выделяют некоторые объекты , для которых определяют моменты изменений или своих состояний. В качестве таких объектов выступают : источники заявок , устройства памяти ( очереди ) , устройства обслуживания , и.т.д.

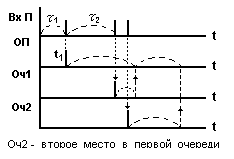
Составим таблицу , отображающую состояние одного из элементов системы

Эта таблица определяет моменты наступления состояний и моменты перехода из одного состояния в другое. Для построения модели из всех значений времени указанных в таблице выбирают минимальное значение по правилу : t : min { t_j } . Если время неизвестно , то задается максимально возможное , т.е   .

Окончание моделирования задается правилом. Если моделрование производится по времени , то таким правилам будет максимальное время. Правило выбора элементов – правило выбора элементов по их приоритету ( задается , т.к. возможно одновременное изменение состояний у двух и более элементов ) . И для выбранного элемента вычисляется новое время и заносится в таблицу. Далее процес продолжается .

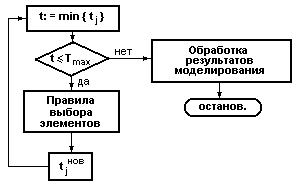
В блоке помимо вычисления нового времени ( t_j^нов ) моделируется и отображение логики моделируемой системы. Т.е. проверяется 6 занят ли прибор или свободен. Если свободен , то вычисляется время окончания обслуживания поступившей заявки и заносится в таблицу . Если прибор уже был занят , то фиксируется время поступления в очередь и для нее определяется величина времени окончания и заносится в таблицу.

Данный метод удобен для сложных систем и может использоваться для системы любого типа.

Метод моделирования с постоянным шагом ( t - метод )

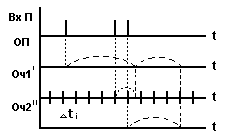
Ось времени делится на интервалы времени const t и задаются правила пересчета состояний элементов системы по правилу : t = t + t. В системе выделяются элементы и определяется изменение состояния ( Да , Нет ) за интервал времени t ( см. метод выше ) .

Шаг t выбирается из условия , чтобы за это время ни один из элементов системы не смог изменить свое состояние дважды . ( При очень маленьком t - возрастает число вычислений ). Применяется для моделирования дискретных устройств систем ( тут t - шаг дискретизации ).