S ( q , w ,  ) - функция качества.

Если канал ненадежен , т.е.  Р – вероятность передачи по каналу , тогда для повторной передачи сообщение будет снова вставать в очередь. Получим модель с обратными связями.

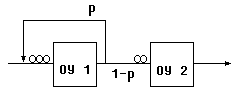
Упрощение моделей

1. Декомпозиция

Производится разбиение системы на подсистемы

В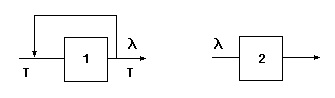сегда можно знать интенсивность потока1 (  ) , поэтому на вторую можем подать поток с уже известной  , если система устойчива.

2. Укрупнение состояний

М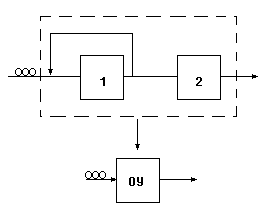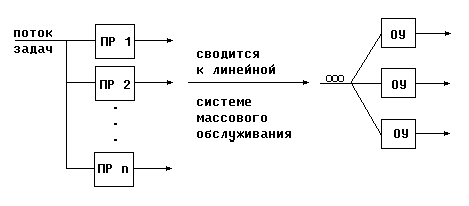ногозадачность и многопроцессорность .

Сообщение – задача

ОУ - процессор

Об’ем очереди = 

Существуют многозначные системы , которые используют мастер-процессор ( процесс в UNIXе ) - производит диспетчеризацию задержек.

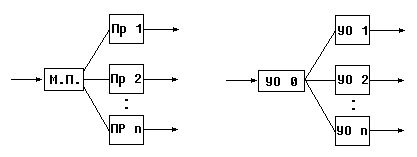
Однозначная многопроцесорная система

III . Дисковые системы raid – системы ( распараллеливают запись информации байта на разные диски ).

Конвейерная обработка

П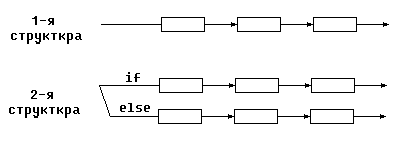рименяется для уменьшения времени при ветвлении.

Нотация Кэнделла

Кэнделл предположил следующую систему обозначений.

М - для обозначения потоков заявок и типов систем массового обслуживания , обладающих Марковскими свойствами ( т.е свойствами отсутствия последствий ).

Потоки Эрланга

Такие потоки обозначают по нотации Кэнделла: Е_к , где к – порядок.

Рассмотрим простейший поток заявок. Потоки Эрланга получаются из простейших путем просеивания.

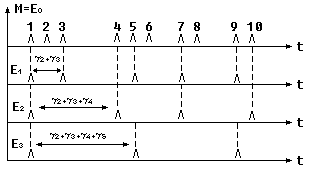
Распределение Эрланга

Плотность распределения вероятностей.

, где k=0..n

Потоки GI (General Independal )

GI - поток общего вида, в котором все  распределены случайно, но независимо друг от друга.

Потоки G

G - произвольный вид распределения. Нет никаких ограничений на законы распределения для каждой заявки.

Длительность обслуживания

Может быть const либо случайной величиной.

Предполагается, что длительность обслуживания подчиняется экспоненциальному закону распределения :

B(x) = 1 - e ^{-  x} , x 0

B(x) =  e ^{-  x}

 - const , характеризующая интенсивность обслуживания ;

B(x) - плотность распределения ;

- среднее время обслуживания .

Такие распределения также обозначают “ М ”.

Длительность обслуживания может подчиняться и другому закону (например Эрланга).

А  В m S … тип системы массового обслуживания по Кенделлу.

1 2 3 4

1. Тип входящего потока.

2. Вид закона распределения длительности обслуживания.

3. Число параллельных каналов.

4. Число мест для ожидания.

Основные типы системы массового обслуживания .

М М  1 - одноканальная система массового обслуживания с простейшим потоком заявок , а обслуживание заявок определяется экспоненциальным законом ( т.к. S =  - система с чистым ожиданием ).

G G  m - многоканальная система массового обслуживания с произвольным потоком заявок и длительностью обслуживания – произвольная с.в.

Граф состояний переходов для системы массового обслуживания .

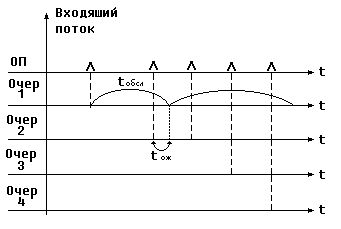
Состояние системы массового обслуживания может быть связано с числом заявок в системе.

При поступлении заявки или на выходе число заявок изменяется, и состояние системы меняется.

Функционирование - процесс перехода системы из одного состояния в другое.

Е_{0 -} нет заявок

Е_{1 -} одна заявка

Е_{2 -} две заявки

Процесс функционирования может быть отображен в виде графа состояний и переходов .

Рассмотрим систему:

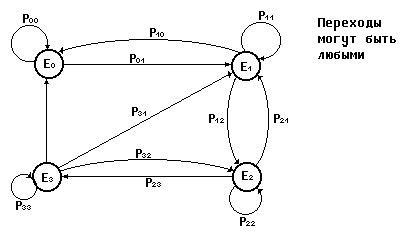
Каждому состоянию приписывают вероятность : Р₀ , Р₁ , …

Т.к. процесс протекает во времени , то вероятности - функции от времени :

Р₀ ( t ) , Р₁ ( t ) , … - это совокупность вероятностей.

Закон распределения состояний системы массового обслуживания

По вероятностям состояний могут быть определены вероятности переходов P_{k l} ( t ) .

Анализ ситемы массового обслуживания состоит в том , чтобы найти распределение состояний Р₀ … Р_n по заданным вероятностям переходов. Через Р₀ … Р_n определяются показатели эффективности системы.

Общий подход к определению вероятностей

Уравнение Колмогорова –Чепмена :

Вычтем из левой и правой части P_k ( t )

Разделим на 

;

Берем 

 _{k k} ,  _{l k} - интенсивность переходов.

Для стационарного состояния :

- условие нормировки

Рассмотрим одноканальную систему массового обслуживания с отказом “ M M 1 S “, где S=0 :

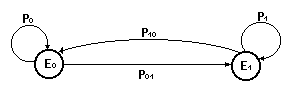
Вывод вероятностей напоминает правила Кирхгофа.

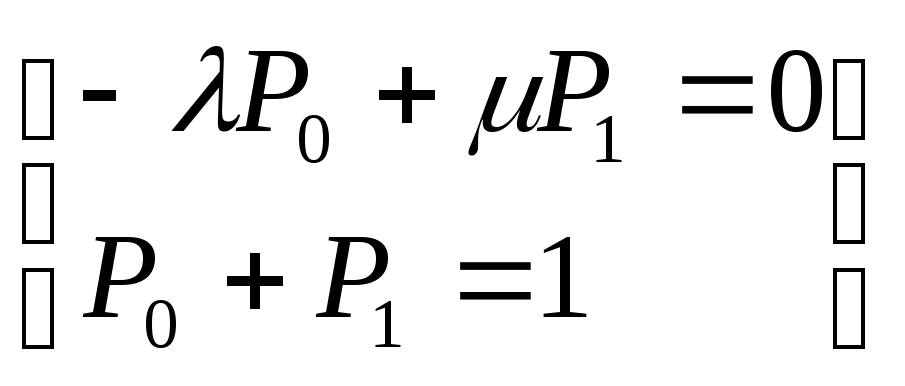
 - среднее число заявок , поступающее за среднее время (длительность ) обслуживания.

Вероятность отказа в обслуживании ( вероятность потери заявки ) в такой системе совпадает с вероятностью того , что состояние системы является состояние Е₁ ( т.е обслуживающий прибор занят )

Р ₁ - вероятность отказа в обслуживании.

Р ₀ - вероятность отказа того , что любая заявка , поступившая в систему будет обслужена.

Система массового обслуживания “ М М 1 S “ ( S =  )

Т.е. всегда существует место в очереди.

Описание системы :

1. Это одноканальная система массового обслуживания с чистым ожиданием.

М М  длительность обслуживания подчиняется экспоненциальному  з-ну с параметром  .

Входящий поток

Простейший ,

С параметром 

2. Построим график состояния переходов.

• Е₀ - в системе нет заявок

• Е₁ - в системе одна заявка

• …

• Е _к-1

• Е _к

• Е _к+1

• _…

Очередь может возрастать до  , а значит число состояний системы тоже  , но счетное ( т.е существует нумерация ) .

 вероятности состояний :

Р₀ ( t ) , P₁ ( t ) , … , P_k ( t ) , тогда стационарные вероятности состояний :

Р₀ , P₁ , … , P_{k -1} , P_k , P_{k + 1 .}

Поток обладает свойством ординарности ( т.к. он простейший ) возможен переход только между соседними состояниями.

3. Вычислим вероятности переходов.

P₀ : P₀₁ = 

P₀₀ =1 - 

P_k : P_{k , k+1} = 

P_{k , k-1} = 

P_{k , k} = 1- (  +  ) 

4. Составим уравнения для нахождения вероятностей

P₀ ( t+ ) = P₀ ( t ) P₀₀ (  ) + P₁ ( t ) P₁₀ (  )

P_k ( t+ ) = P_k-1 ( t ) P_{k-1 , k} (  ) + P_k ( t ) P_{k , k} (  ) + P_k+1 ( t ) P_{k+1 , k} (  ) , для k = 1, 2 …  .

Вычтем Р_к ( t ) из левой и правой части , и разделим на  , и перейдем к :

Если , т.е стационарное состояние системы , то получим систему уравнений в стационарном состоянии:

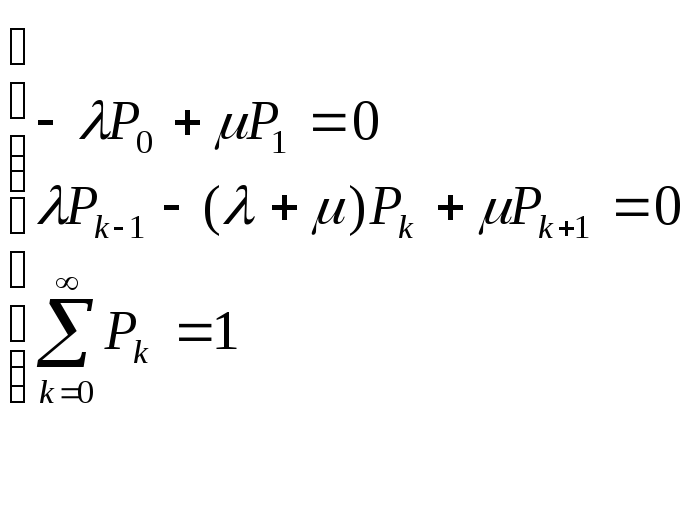
Для ее решения можем представить формулу 2 в виде :

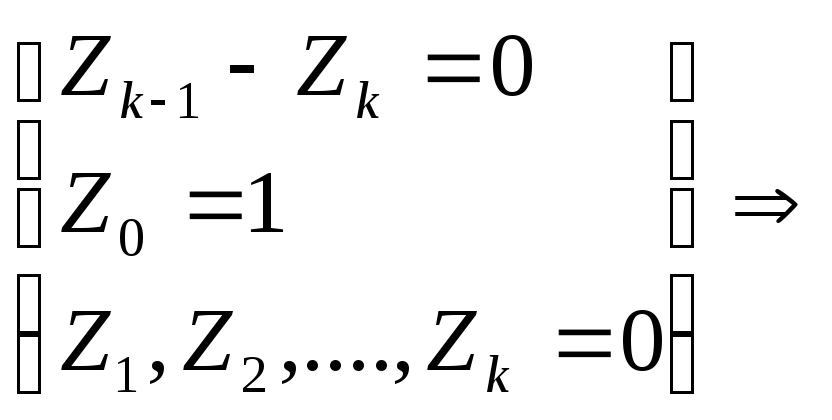для любого k , Z _k = 0

Рекуррентное вычисление вероятностей нам даст :

Вероятность Р₀ найдем из условия нормировки , для этого представим в виде :

Где  ^к = 1 +  + ² + ³ + … = геометрическая прогрессия = 

Р₀ = 1 -   Р_к = ^к ( 1 -  ) - вероятность обслуживания заявок без ожидания.

Справедливо только для убывающей геометрической прогрессии   < 1 

Нагрузка на систему должна быть меньше 1 , только тогда ряд сходится и существует стационарное распределение состояния , иначе очередь будет возрастать неограниченно.

 - загрузка ( нагрузка ) системы ;

  _{о ж}  0  = 1 – Р₀ =  - среднее число заявок , поступивших за время обслуживания.

5. Вычисление характеристик ( показателей эффективности )

• среднее время ответа

• среднее время ожидания

• средняя длина очереди

t _отв = t _ож + t _обсл

Среднее время ожидания – время от момента поступления заявки до момента начала ее обслуживания.

Средняя длина очереди - среднее число заявок , находящихся в системе и ожидающие начала обслуживания.

При выборе модели нужно оценивать последствия выбора.