Среднее число заявок в очереди :

Среднее время ответа :

Закон сохранения интенсивности потока

Интенсивность входящего потока заявок в систему равняется интенсивности выходящего потока.

G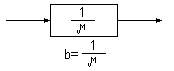 G  1

Пусть 1 – Р₀ - вероятность того , что прибор занят.

 ( 1 – Р₀ ) -интенсивность выходящего потока заявок.

По закону сохранения интенсивности потока можно записать :  =  ( 1 – Р₀ ) , отсюда

( см. М М 1 )

Не зависит от интенсивности потока и времени ожидания.

В системах массового обслуживания выполняется закон сохранения времени ожидания :

 _i - коэффициент загрузки

w _i - длительность ожидания

i - номер входящего потока

Вывод : Этот закон означает , что С.М.О с ожиданием (без потерь ) инвариантны относительно дисциплины обслуживания , т.е. если потерь заявок в системе нет , то не зависимо от дисциплины обслуживания это выражение остается const.

О.С стремится занять всю память и все возможные ресурсы системы.

Формулы Литтла

Это все ( G  G 1 )

, где

- среднее число заявок в системе

- среднее число заявок в очереди

- средняя длительность отклонения

( M  G  1 ) Полачика – Хингина

b² - второй начальный момент обслуживания заявок.

Пример ( для экспоненциальной длительности обслуживания ) :

Процесыы рождения ( размножения ) и гибели .

Пусть исследуемая система может находится в одном из состояний Е₀ , Е₁ , Е₂ …

В системе возможны переходы между соседними состояниями.

_к  + о (  )



Е_{к – 1} Е_к Е_{к + 1}



_к  + о (  )

Е_к  Е_к : 1 – (_к + _к )  + о (  ) - отсутствие изменений.

О (  ) - бесконечно малая , порядка выше , чем  , т.е

Если все _к =0 , то в такой системе возможны только переходы : Е_{к – 1}  Е_к  Е_{к + 1} - процесс чистого размножения .

Если все _к =0 , то это процесс гибели.

Для стационарного режима можно записать уравнения для вычисления параметров состояния :

Раскрывая скобки и сгруппировав , получим

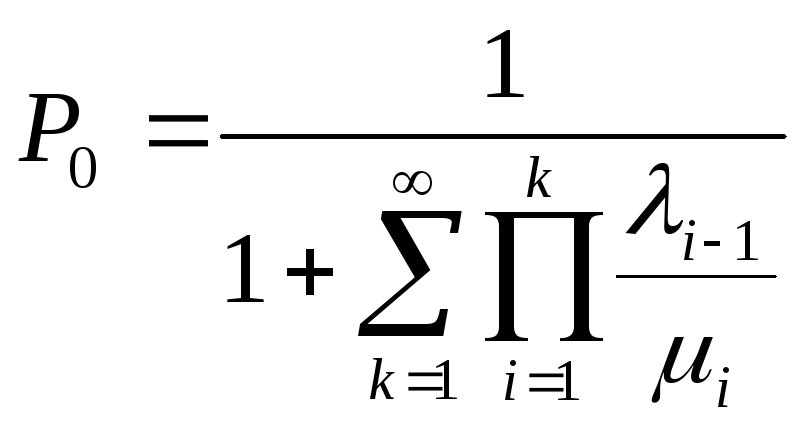, где - условие сходимости.

Существование стационарного режима возможно , что ряд Р₀ - сходится.

Это требование аналогично убывающей геометрической прогрессии для системы М М 1.

Процессы гибели – размножения могут служить моделями для СМО и можно воспользоваться готовыми файлами для вычисления вероятностей.

Чтобы воспользоваться готовыми формулами, необходимо установить соответствие между ними.

Исследование СМО ММ1 с помощью процессов рождения и гибели ( ПРГ ).

Необходимо установить между параметрами _к и _к ПРГ с одной стороны и параметрами исследуемой СМО  ,  , M , S , где

 - интенсивность входного потока

1. _- интенсивность выходного потока

M - число обслуживающих приборов

S -

_к =  для всех k

_к =  для любого k

В этой системе S =  , т.е любая заявка будет обслужена.

Воспользуемся формулой рождения и гибели процессов для вычисления :

, т.к  _i = const =  ,  _{i – 1} = const =  , то

k = 1 

k = 2 

, учитывая , что  _i = const =  ,  _{i – 1} = const =  , то

, тогда ( т.к - коэффициент загрузки ) , то

Т.к , то

Вывод : Процессы рождения и гибели могут быть использованы для анализа СМО.

Вероятность любого состояния : или

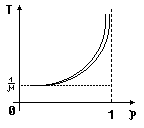Т - Время ответа

 - Коэффициент загрузки системы ,   0 , 1 ) для стационарной системы.

- Среднее время обслуживания

Система массового обслуживания типа M M 1 , где S – конечна.

Цель анализа системы :

1. Получение вероятности состояний

2. Определение характеристик системы.

Существуют вероятности :

• потери заявки

• отказы в обслуживании

Для вычисления вероятностей состояний воспользуемся аналогиями процессов рождения и гибели.

Д.З !!!!!!!

Многоканальная Система Массового Обслуживания с отказами

Система с

m - обслуживающее устройство

1. - поток входных заявок

1. - поток выходных заявок

Т.к система с отказами , то в ней заявка может занимать любой свободный прибор

( если он есть ) , если свободных нет , то все заявки , поступающие в период занятости системы , получают отказ и будут потеряны.

Установим аналогию между параметрами процесса рождения – гибели и этой системы.

Построим граф состояний и переходов:

Е_{0 -} Нет заявки

Е_{1 -} Одна заявка

Е_{m -} Все приборы заняты

• общее число состояний ограничено числом приборов  всего состояний m+1.

Переходы в системе : E_i  E _i+1

Интенсивность переходов ( E_i  E _i+1 ) постоянны и равны ; _к= , для к=0…( m-1)

Переходы в системе : E _i+1  E_i связаны с окончанием обслуживания заявки.

интенсивность перехода зависит от номера состояния. Чем больше число приборов, тем вероятность обслуживания выше.

- вероятность обслуживания хотя бы одной заявки , где

1. - время перехода

k - число занятых приборов

Для ПРГ:

, для k=1…m

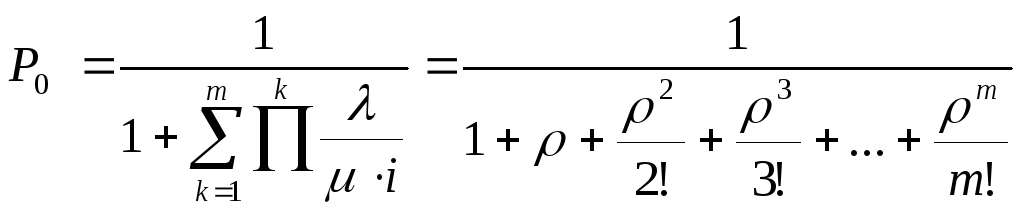( 1)

, где *2*3 =k!  ( 2)

Формулы ( 1) и ( 2) называют формулами Эрланга , а сама задача - задача Эрланга.

Основной характеристикой такой системы является - вероятность отказа , когда система находится в состоянии Е_{m .}

Вероятность обслуживания заявки:

Эта характеристика характеризует относительную пропускную способность системы.

Пример : С.М.О для некоторой ВС. ( Модель ВС )

ВС состоит из ряда терминалов клиентских машин , сервера + соединение

Т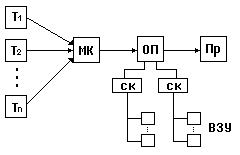₁ … Т_n - терминалы

ОП - оперативная память

Пр - процессор

МК - мультиплексорный канал

СК - селектор каналов ( механизм обращения к ЗУ )

ВЗУ - внешнее запоминающее устройство

Для обработки каждой задачи выделяется некоторый квант времени.

Наряду с СМО рассматривают и Сети Массового Обслуживания ( СтМО ).

При построении модели этой системы выделяют ряд отдельных СМО , связанных между собой и образующих Сеть Массового Обслуживания ( СтМО ). Такие сети называют стохастическими. Анализ таких сетей более сложен.

СтМО могут быть как замкнутыми , так и разомкнутыми.

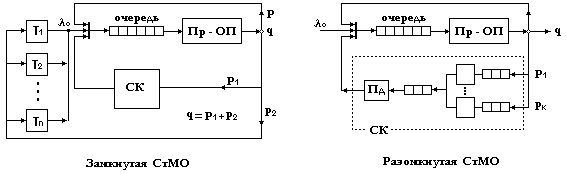
Т - терминалы ( источники заявок )

₀ - максимальная суммарная интенсивность потока заявок

Для замкутой СтМО:

Диспетчер выбирает заявку , и на время кванта ее обслуживает Пр – ОП .

Если заявка не обслужена ( время обслуживания не закончено ) , то с вероятностью Р заявка возвращается в конец очереди.

С вероятностью q заявка может требовать либо обращение к ОП ( Р₁ ) , либо может быть обслужена с вероятностью Р₂ .

Для разомкутой СтМО:

₀ - потока заявок постоянной интенсивности .

q - вероятность того , что обслуживание заявки будет закончено и она покинет систему обслуживания.

Имитационное моделирование

Имитационная модель (ИМ) – алгоритм или программа, которая с помощью тех или иных средств (могут быть квадратики, скобочки, и т.п. ) описывают, воспроизводят, моделируют и в конечном счете имитируют процесс функционирования системы, воспроизводя временную диаграмму, процесс функционирования.

Исследование ИМ производится с помощью методов статистических испытаний,

например, с помощью метода Монте – Карло .

Имитационное моделирование - построение процесса, который имитирует реальный.

Адекватность – правильность моделирования. Модель должна быть адекватной исходному объекту.

Моделирование – процесс создания и исследования модели. Имитационные модели обычно бывают вероятностными и статистическими. Процесс исследования носящий вероятностный характер называют методом статистических испытаний ( или метод Монте – Карло ).

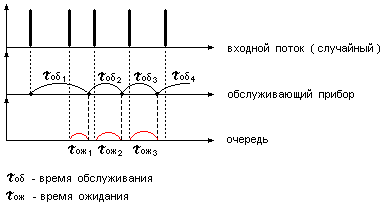Пример: ( Статистическое моделирование, которое является моделью (система с ожиданиями ) ).

Если описать формально эту диаграмму с помощью специального языка, то это и будет модель.

Основой для построения имитационной модели является - построение диаграммы.