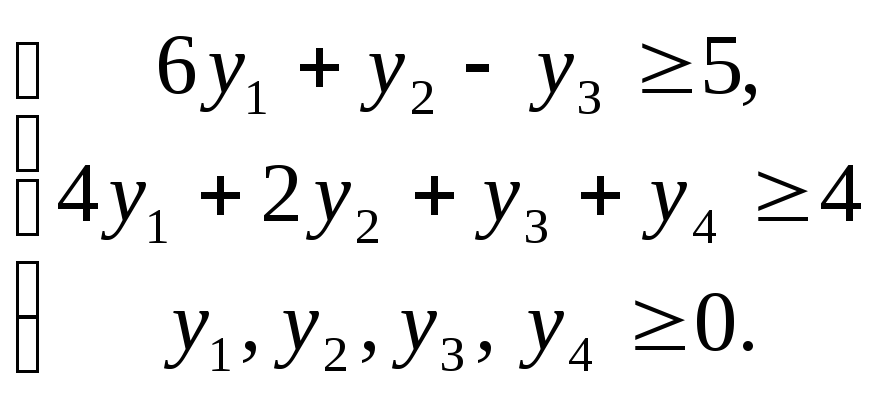2. Анализ чувствительности

Анализ чувствительности выполняется уже после получения оптимального решения задачи ЛП. Его цель – определить, приведет ли изменение коэффициентов исходной задачи к изменению текущего оптимального решения, и если да, то как эффективно найти новое оптимальное решение (если оно существует).

В общем случае изменение коэффициентов исходной задачи может привести к одной из следующих ситуаций:

1. Текущее базисное решение остается неизменным.

2. Текущее решение становится недопустимым.

3. Текущее решение становится неоптимальным.

4. Текущее решение становится неоптимальным и недопустимым.

Во второй ситуации можно использовать двойственный симплекс-метод для восстановления допустимости решения. В третьей ситуации мы используем прямой симплекс-метод для получения нового оптимального решения. В четвертой ситуации для получения нового оптимального и допустимого решения следует воспользоваться как прямым, так и двойственным симплекс-методом. Четвертая ситуация, как комбинация второй и третьей, будет рассмотрена позже.

Для объяснения различных процедур анализа чувствительности используем пример 1.1 производства краски.

Исходная задача	Двойственная задача

Приведем также последнюю симплекс-таблицу этого примера.

Базис	z	x1	x2	s1	s2	s3	s4	Решение
z	1	0	0	3/4	1/2	0	0	21
х1	0	1	0	1/4	-1/2	0	0	3
х2	0	0	1	-1/8	3/4	0	0	3/2
s3	0	0	0	3/8	-5/4	1	0	5/2
s4	0	0	0	1/8	-3/4	0	1	1/2

3.2.1 Изменения, влияющие на допустимость решения

К недопустимости текущего оптимального решения может привести как изменение правых частей ограничений (т.е. изменение элементов вектора b), так и введение во множество ограничений задачи нового ограничения. В любом случае недопустимость решения проявится в том, что, по крайней мере, один элемент в векторе В^-1b станет отрицательным, т.е. одна или несколько базисных переменных примут отрицательное значение.

Изменение элементов вектора b правых частей ограничений

Предположим, что предприятие хочет ежедневно увеличить приобретение первого сырья М1 до 28 тонн. Как это изменение повлияет на максимальный доход предприятия? По формуле Х_В=В^-1b и найдем новое решение задачи.

Таким образом, текущие базисные переменные с новыми значениями по-прежнему составляют допустимое решение. Соответствующее этому решению оптимальное значение целевой функции равно 24 тыс.руб.

Если увеличить ежесуточное приобретение второго сырья М2 до 8 тонн, оставляя сырье М1 на прежнем уровне 24 тонны, то получим совсем другую картину.

Полученное решение не является допустимым, поскольку s₄=-1. Для возврата в область допустимых решений применим двойственный симплекс-метод для соответствующей симплекс-таблицы. Отметим, что она отличается от последней симплекс- таблицы примера 1.1 только столбцом «Решение».

Базис	z	x1	x2	s1	s2	s3	s4	Решение
z	1	0	0	3/4	1/2	0	0	22
х1	0	1	0	1/4	-1/2	0	0	2
х2	0	0	1	-1/8	3/4	0	0	3
s3	0	0	0	3/8	-5/4	1	0	0
s4	0	0	0	1/8	-3/4	0	1	-1

В соответствии с двойственным симплекс-методом исключаемой переменной будет s₄, а вводимой – s₂. В результате получим следующую симплекс-таблицу с оптимальным допустимым решением. (В общем случае для получения оптимального решения может потребоваться несколько итераций двойственного метода).

Базис	z	x1	x2	s1	s2	s3	s4	Решение
z	1	0	0	5/6	0	0	2/3	64/3
х1	0	1	0	1/6	0	0	-2/3	8/3
х2	0	0	1	0	0	1	0	2
s3	0	0	0	1/6	0	1	-5/3	5/3
s2	0	0	0	-1/6	1	0	-4/3	4/3

Интервалы допустимых изменений для элементов b

Другой способ исследования влияния изменения доступности ресурсов (т.е. элементов вектора b правых частей неравенств ограничений) заключается в определении интервалов допустимости для этих элементов, сохраняющих текущее решение допустимым.

Заменим вектор b вектором

Для того чтобы текущее базисное решение осталось допустимым, необходимо выполнение неравенства Х_В=В^-1b₁>=0. Отсюда получаем следующую систему неравенств:

Первое неравенство порождает второетретьеи четвертое. Это эквивалентно следующему двойному неравенству для приращенияТаким образом интервал допустимости дляb₁ получается следующий: .

Аналогично получим интервал допустимости и для b₂

Тогда

Первое неравенство порождает второетретьеи четвертое. Это эквивалентно следующему двойному неравенству для приращенияТаким образом интервал допустимости дляb₂ получается следующий: .

Если сравнивать этот результат для интервалов допустимости для ресурсов с результатами элементарного графического исследования на чувствительность, проведенного в теме 1, то можно обнаружить точное совпадение.

Определение интервалов допустимости для ресурсов b_i вышеприведенным способом корректно только когда изменения рассматриваются независимо друг от друга, только тогда в пределах интервала допустимости ресурсаb_i итоговое приращение целевой функции (что следует из первой теоремы о двойственности) пропорционально приращению ресурса и двойственной цене ресурса.

Одновременное изменение ресурсов намного сложнее, ведь приходится решать линейную систему неравенств от многих переменных. Поэтому при изменении сразу нескольких ресурсов, ведущих к недопустимому решению, следует применить двойственный симплекс-метод и получить новое решение и значение целевой функции и сравнить с прежним решением.

Добавление новых ограничений

Добавление нового ограничения в существующую модель ЛП может привести либо к ситуации, когда ограничение избыточное, когда оно выполняется при текущем оптимальном решении, тогда ограничение просто отбрасывается, либо к ситуации, когда новое неравенство не выполняется при текущем оптимальном решении, тогда необходимо применить двойственный симплекс-метод, чтобы получить новое оптимальное решение.