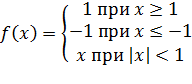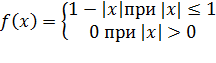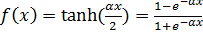7.2 Функции активации в нейронных сетях
Функция активации
(активационная функция, функция
возбуждения) – функция, вычисляющая
выходной сигнал искусственного нейрона.
В качестве аргумента принимает сигнал
,
получаемый на выходе входного сумматора
.
Результатом будет являться выходной
сигнал нейрона 
.
Ниже приведен наиболее общий список
функций активации.
1 Единичный скачок или жесткая пороговая функция
Простая кусочно-линейная функция. Если входное значение меньше порогового, то значение функции активации равно минимальному допустимому, иначе – максимально допустимому (рисунок 7.2).
|
Единичная |
|
|
(7.5) | |
|
Знаковая (биполярная) |
|
|
(7.6) | |
|
|
|
|
| |
|
Единичная |
Знаковая (биполярная) | |||
|
|
| |||
|
Рисунок 7.2 – Единичный скачок или жесткая пороговая функция | ||||
2 Линейная пороговая функция
Несложная кусочно-линейная функция. Имеет два линейных участка, где функция активации тождественно равна минимально допустимому и максимально допустимому значению и есть участок, на котором функция строго монотонно возрастает (рисунок 7.3).
|
Линейная |
|
|
(7.7) | |
|
Линейная с насыщением |
|
|
(7.8) | |
|
Полулинейная |
|
|
(7.9) | |
|
Полулинейная с насыщением |
|
|
(7.10) | |
|
Треугольная |
|
|
(7.11) | |
|
|
|
|
| |
|
Линейная |
Линейная с насыщением | |||
|
|
| |||
|
Полулинейная |
Полулинейная с насыщением | |||
|
|
| |||
|
Треугольная | ||||
|
| ||||
|
Рисунок 7.3 – Линейная пороговая функция | ||||
3 Сигмоидальная функция или сигмоид
Монотонно возрастающая всюду дифференцируемая -образная нелинейная функция с насыщением. Сигмоид позволяет усиливать слабые сигналы и не насыщаться от сильных сигналов. Гроссберг (1973 год) обнаружил, что подобная нелинейная функция активации решает поставленную им дилемму шумового насыщения.
Слабые сигналы нуждаются в большом сетевом усилении, чтобы дать пригодный к использованию выходной сигнал. Однако усилительные каскады с большими коэффициентами усиления могут привести к насыщению выхода шумами усилителей, которые присутствуют в любой физически реализованной сети. Сильные входные сигналы в свою очередь также будут приводить к насыщению усилительных каскадов, исключая возможность полезного использования выхода (рисунок 7.4).
|
Логистическая или экспоненциальная сигмоида |
|
(0,1) |
(7.12) |
|
Гиперболический тангенс |
|
(–1,1) |
(7.13) |
|
Рациональная сигмоида |
|
(–1,1) |
(7.14) |
где
– параметр наклона сигмоидальной
функции активации. Изменяя этот
параметр, можно построить функции с
различной крутизной.
|
Логистическая или экспоненциальная сигмоида |
Гиперболический тангенс и рациональная сигмоида |
|
|
|
|
Рисунок 7.4 – Сигмоидальная функция или сигмоид | |
4 Радиально-базисная функция
Этот тип функций принимает в качестве аргумента расстояние между входным значением и некоторым наперед заданным центром активационной функции. Значение этой функции тем выше, чем ближе входной вектор к центру (рис 7.5).
|
Радиально-базисная |
|
(0,1) |
(7.15) |
где
– параметр определяет скорость спадания
функции при удалении вектора от центра
и называетсяшириной
окна; 
– параметр определяет сдвиг активационной
функции по оси абсцисс.
|
Радиально-базисная |
|
|
|
Рисунок 7.5 – Радиально-базисная функция |
В заключение отметим, что функции активации типа единичного скачка и линейного порога встречаются очень редко и, как правило, используются на учебных примерах. В практических задачах почти всегда применяется сигмоидальная функция активации.