85

А.С.Михайлов

Методы оптимизации

Красноярск 2012

Министерство образования и науки Российской Федерации

ФГБОУ ВПО «Сибирский государственный технологический университет»

А.С.Михайлов

Методы оптимизации

Рекомендовано редакционно-издательским советом СибГТУ в качестве курса лекций для студентов направления 230100.68 «Информатика и вычислительная техника»

Красноярск 2012

Михайлов А.С. Методы оптимизации: курс лекций для студентов направления 230100.68 «Информатика и вычислительная техника» очной формы обучения / А.С.Михайлов. – Красноярск: СибГТУ, 2012. – 81с.

Рецензенты:

ст.преподаватель Е.Н.Касьянова (научно-методический совет СибГТУ),

д-р техн. наук, проф. А.В.Медведев (СибГАУ)

Курс лекций предназначен для углубленного изучения дисциплины «Методы оптимизации», содержит доказательства теорем и оснащено многочисленными поясняющими примерами. В нем содержится обширный список литературы для самостоятельного изучения дисциплины. Пособие может быть использовано студентами при выполнении лабораторных работ по дисциплинам «Теория принятия решений» и «Исследование операций», а также преподавателями и аспирантами.

© А.С.Михайлов, 2012

© ФГБОУ ВПО «Сибирский государственный технологический университет», 2012

СОДЕРЖАНИЕ

Введение 5

Лекция 1 Симплекс-метод 6

1.1 Общая постановка задачи линейного программирования 6

1.2 Некоторые свойства планов 7

1.3 Алгоритм симплекс-метода 9

Лекция 2 Двойственная задача. Двойственный симплекс-метод. Комбинированный метод решения ЗЛП 14

2.1 Постановка двойственной задачи 14

2.2 Основные теоремы о двойственности 16

2.3 Решение двойственных задач 17

2.4 Двойственный симплекс-метод 18

Лекция 3 Анализ чувствительности оптимального решения 21

3.1 Матричное представление симплекс-таблиц 21

3.2 Анализ чувствительности 24

Лекция 4 Целочисленное линейное программирование 30

4.1 Метод ветвей и границ 30

4.2 Метод отсекающих плоскостей 35

Лекция 5 Методы решения транспортной задачи 39

5.1 Решение транспортной задачи 39

5.2 Задача о назначениях 46

Лекция 6 Введение в нейронные сети 49

6.1 История нейронных сетей 49

6.2 Актуальность нейронных сетей 51

6.3 Свойства нейронных сетей 52

6.4 Классификация нейронных сетей 52

6.5 Представление знаний в нейронных сетях 53

Лекция 7 Биологическая и математическая модель нейрона. Персептрон 57

7.1 Модель нейрона 57

7.2 Функции активации в нейронных сетях 59

7.3 Обучение нейронной сети 63

7.4 Персептрон 64

Лекция 8 Алгоритм обратного распространения ошибки 70

8.1 Многослойные нейронные сети. Структура 70

8.2 Вывод основных формул алгоритма обратного распространения ошибки 72

Лекция 9 Рекуррентный метод наименьших квадратов 77

9.1 Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей (RLS) 77

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 82

Заключение 83

Приложение А 84

Введение

Целью данного курса лекций является помощь студентам в приобретении знаний по теоретическим основам методов оптимизации и получении твердых навыков решения практических задач.

Для достижения этой цели в курсе изложены основные понятия, определения, теоремы методов оптимизации, приведены примеры решения типовых задач.

Особое внимание уделено теории двойственности и связанных с ней двойственному симплекс-методу, матричному представлению симплекс-метода, с помощью чего подробно излагается анализ на чувствительность линейных задач.

Кроме того, рассматриваются методы целочисленного программирования: метод ветвей и границ и метод отсечения, а также метод потенциалов для решения транспортных задач и венгерский метод для решения задачи о назначениях.

Также приводятся основные понятия и алгоритмы нейронных сетей: персептрон, алгоритм обратного распространения ошибки и рекуррентный метод наименьших квадратов (RLS), который практически не используется в России.

Материал изложен логически последовательно, в доступной для студентов форме, по возможности сопровождается доказательствами теорем и многочисленными примерами решения задач.

Успешное освоение данного курса лекций по дисциплине «Методы оптимизации» способствует формированию общекультурной компетенции:

(ОК-10) – умение использовать основные законы естественнонаучных дисциплин в профессиональной деятельности и применять методы математического анализа и моделирования, теоретического и экспериментального исследования.

Материал, изложенный в курсе лекций, изучается на 2 курсе магистратуры в II семестре дисциплины «Методы оптимизации» в объеме 18 часов лекционных и 36 часов лабораторных занятий, приведенных в сборнике заданий «Методы оптимизации. Линейное и сетевое программирование» и лабораторном практикуме «Методы оптимизации» [3].

Лекция 1 Симплекс-метод

План

1. Общая постановка задачи линейного программирования

2. Некоторые свойства планов

3. Алгоритм симплекс-метода

1.1 Общая постановка задачи линейного программирования

Общая форма задачи линейного программирования (ЛП) обычно записывается следующим образом:

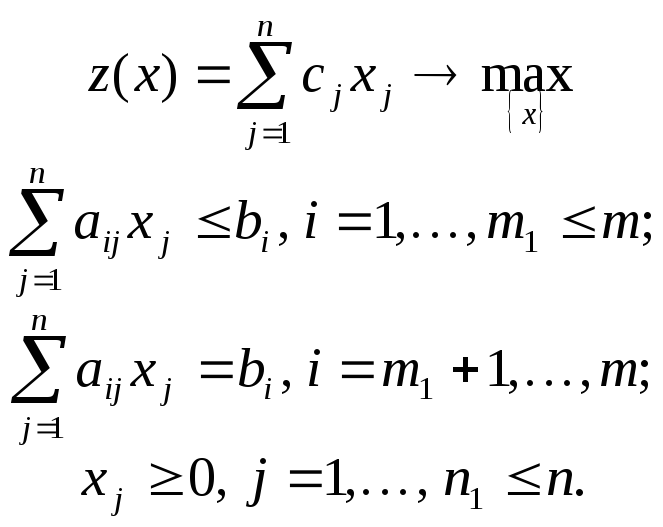
(1.1)

Условия задачи (1.1) называются смешанными, ибо в них присутствуют ограничения типа равенств и типа неравенств.

В матричной форме задача ЛП (1.1) приобретает вид

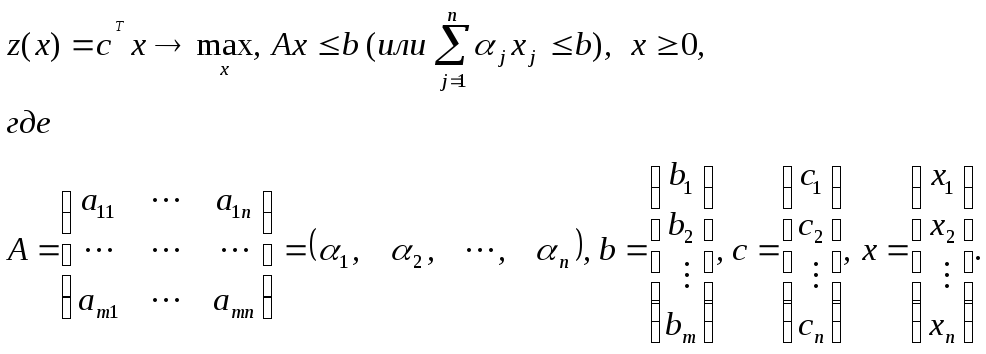(1.2)

Набор чисел x₁, x₂, …, x_n, или вектор x, удовлетворяющий системе ограничений, называется планом рассматриваемой задачи ЛП. Компоненты вектора х называются составляющими плана.

Каждому плану х соответствует определенное значение функции z(x). Чем больше z(x), тем лучше план. План, для которого z(x) достигает максимума, называется оптимальным планом х₀, т.е. z(x₀) ≥ z(x), где х- любой план задачи (1.1).

В дальнейшем будем предполагать, что область допустимых планов – ограничена и непуста.

В теории ЛП рассматривают три формы задачи ЛП:

1. каноническую 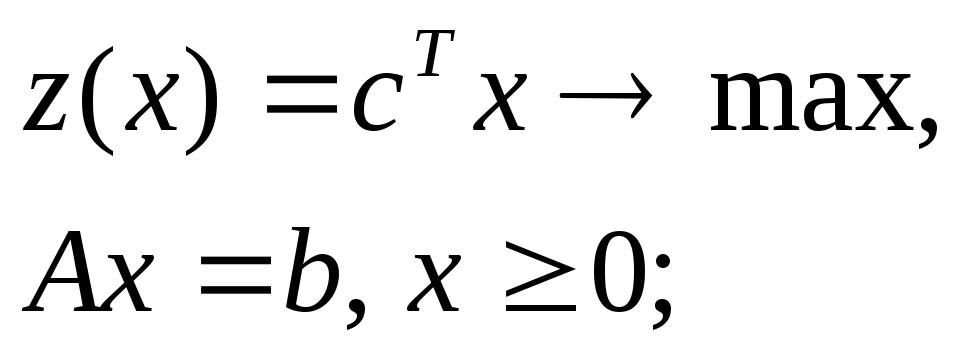(1.3)

2. сопряженную каноническую

3. форму с однотипными ограничениями

Покажем теперь, что любую линейную задачу можно привести к канонической форме. Для этого необходимо научиться переходить от ограничений типа неравенств к ограничениям типа равенств и от переменных х_j, на которые не наложено условие неотрицательности, к неотрицательным переменным.

1. Каждое неравенство переходит в равенство при сложении левой части неравенства с новой неотрицательной переменной

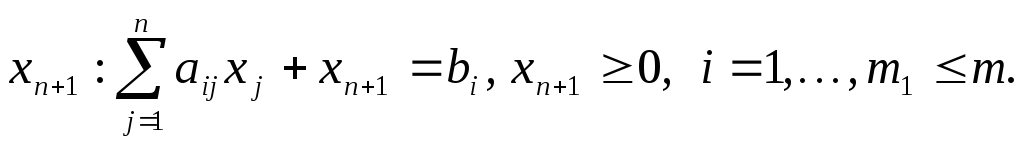
2. Если n₁<n, то каждая переменная 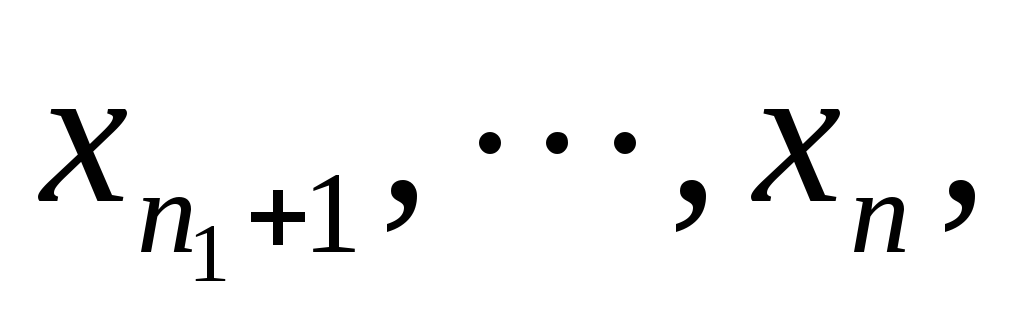на которую не наложено условие неотрицательности, заменяется разностью новых неотрицательных переменных

Пример 1.1 Привести к канонической форме записи задачу ЛП

x₁+x₂=max, -x₁+x₂ ≤ -1, 2x₁+x₂=2, x₁ ≥ 0, x₂-свободная переменная.

Первое ограничение запишем в форме равенства введением новой переменной х₃≥0: -x₁+x₂+х₃=-1. Так как на x₂ не наложено условие неотрицательности, то заменяем х₂ разностью двух новых неотрицательных переменных После этих преобразований исходная задача ЛП запишется в канонической форме: