Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

08-МУ к лаб_занятиям

.pdf

Скачиваний:

Добавлен:

04.06.2015

Размер:

1.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Порядок выполнения работы

1.Составить математическую модель в виде задачи целочисленного программирования. Предварительно указать все возможные способы распила доски на заготовки нужной длины.

2.Решить задачу с применением Excel.

3.Проанализировать полученное решение.

4.Оформить отчет по лабораторной работе, который должен содержать:

∙название работы;

∙исходные данные варианта;

∙построенную модель задачи;

∙результаты и анализ решения задачи.

Задание

Доски длиной L следует распилить на заготовки двух видов: длиной l1 и длиной l2 . Заготовок первого вида должно быть получено не менее n1 штук, заготовок второго вида – не менее n2 штук. Каждая доска может быть распилена на указанные заготовки несколькими способами. Определить, сколько досок надо распилить каждым способом, чтобы необходимое количество заготовок было получено из наименьшего числа досок.

Таблица 11 –	Варианты исходных данных
№ варианта	L,м	l1,м	l2,м	n1	n2
1	2	3	4	5	6
1	4,0	1,5	1,1	92	55
2	4,6	1,9	1,3	60	65
3	4,5	1,7	1,3	94	55
4	3,8	1,5	1,1	70	67
5	4,0	1,6	1,1	32	57
6	3,7	1,4	1,1	45	65
7	4,8	1,9	1,3	42	47
8	4,0	1,5	1,2	87	67
9	4,1	1,6	1,1	50	51
10	3,3	1,4	0,9	88	61
11	4,4	1,6	1,3	89	75
12	4,7	2,0	1,3	68	53
13	3,6	1,5	1,0	93	61
14	4,8	1,9	1,4	62	51
15	4,5	1,9	1,2	88	63
16	3,1	1,3	0,8	53	55
17	3,2	1,2	0,9	97	43
18	3,7	1,4	1,0	83	67
19	3,3	1,4	0,9	59	43
20	3,7	1,4	1,1	94	59

Контрольные вопросы

1.Математическая модель задачи целочисленного программирования.

2.Этапы решения задачи в табличном редакторе MS Excel.

3.Как составить математическую модель задачи раскроя досок?

4.Какие величины являются искомыми в задаче раскроя досок?

5.Как записать целевую функцию задачи?

6.Как составить ограничения задачи?

7.Какая информация содержится в отчете о результатах для данной задачи?

8.Какую информацию содержит отчет по устойчивости?

Лабораторная работа № 8 Решение задачи о назначениях

Цель работы: Приобретение умения решать задачу о назначениях с использованием табличного процессора Microsoft Excel.

Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно- исследовательским лабораториям и т.п. В этой задаче для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.д.), а каждый ресурс может быть использован на одной и только одной работе. То есть ресурсы не делимы между работами, а работы не делимы между ресурсами. Задача о назначениях является частным случаем транспортной задачи.

Исходные параметры модели задачи о назначениях

1.n – количество ресурсов, m – количество работ.

2.ai = 1 – единичное количество ресурса Ai ( i = 1,n ), например: один работник; одно транспортное средство; одна научная тема и т.д.

3. b j = 1 – единичное количество работы B j ( j = 1,m ), например: одна должность; один маршрут; одна лаборатория.

4. cij	–	характеристика качества выполнения работы B j с помощью
ресурса	Ai .	Например, компетентность i-го работника при работе на j-й

должности; время, за которое i-е транспортное средство перевезет груз по j- му маршруту; степень квалификации i-й лаборатории при работе над j-й научной темой.

Искомые параметры

1. xij – факт назначения или неназначения ресурса Ai на работу B j :

0, если i - й ресурс не назначен на j - ю работу,

xij =

1 , если i - й ресурс назначен на j - ю работу.

2. F (X ) – общая (суммарная) характеристика качества распределения ресурсов по работам.

Математическая модель задачи о назначениях

n	m
F (X ) = ∑∑cij xij → min ;
i =1	j =1

n
n
∑xij = 1 (i = 1,m),
j =1			(21)
m			(21)

			= 1 (j = 1,n),
∑xij			= 1 (j = 1,n),
i =1			0, (i =			).
		=
x	ij	=		1,m; j =	1,n
	ij		1,

В некоторых случаях,			например, когда cij – это компетентность, опыт

работы или квалификация работников, условие задачи может требовать максимизации целевой функции, в отличие от (21). В этом случае целевую функцию F (X ) заменяют на F1(X ) = −F (X ) и решают задачу с целевой функцией F1 (X ) → min , что равносильно решению задачи с целевой функцией F (X ) → max .

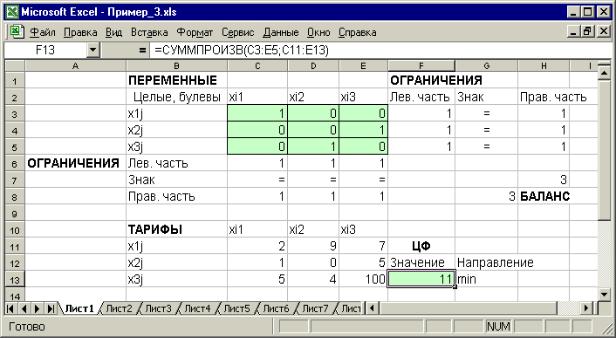
При решении задач о назначении в Excel необходимо учитывать, что переменные xij являются булевыми, то есть могут принимать только одно из

двух значений: 0 или 1. На рисунке 23 представлена экранная форма с решением некоторой задачи с булевыми переменными.

Рисунок 23 - Решение задачи с булевыми переменными

При вводе условия задач с булевыми переменными необходимо:

∙задать требование целочисленности (см. лаб. работу №8);

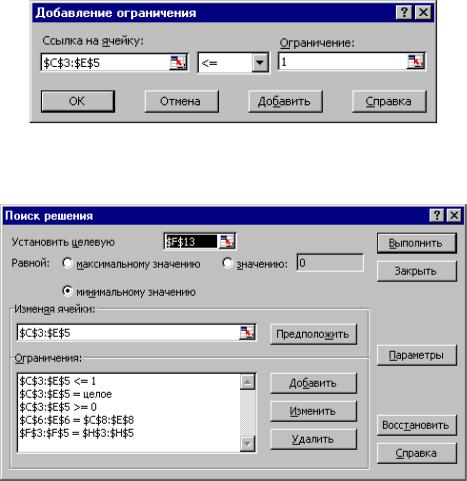
∙в окне Поиск решения добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рисунок 24).

Вид окна Поиск решения для задачи с булевыми переменными, представленной на рисунке 23, приведен на рисунке 25.

Рисунок 24 - Добавление условия единичной верхней границы значений переменных

Рисунок 25 - Окно Поиск решения для задачи с булевыми переменными, представленной на рисунке 23

Порядок выполнения работы

1.Составить математическую модель задачи. Номера новых сотрудников, новых и прежних мест выбираются по вариантам из таблицы 12. Номера прежних мест являются номерами прежних сотрудников. Компетентность новых сотрудников выбирается по таблице 13, компетентность прежних сотрудников – по таблице 14.

2.Найти оптимальное решение в табличном процессоре Microsoft Excel.

3.Сделать анализ полученного решения.

4.Оформить отчет по лабораторной работе, который должен содержать:

∙название работы;

∙исходные данные варианта;

∙построенную модель задачи;

∙результаты и анализ решения задачи.

Задание

Отдел кадров предприятия устроил конкурсный набор специалистов на две вакантные должности. На эти новые места (НМ) претендуют 3 прежних сотрудника (ПС), уже работающие в других отделах, и 4 новых сотрудника

(НС).

Отдел кадров оценил по десятибалльной шкале компетентность новых сотрудников и прежних сотрудников для работы и на новых, и на прежних местах (ПМ). Необходимо учесть, что руководство предприятия, во-первых, предпочитает, чтобы прежние сотрудники не претендовали на места друг друга, и, во-вторых, не намерено увольнять прежних сотрудников.

Необходимо распределить сотрудников по должностям наилучшим образом. Варианты исходных данных приведены в таблицах 12, 13, 14.

Таблица 12 -Номера сотрудников и мест их работы для конкретного варианта

№		Новые сотрудники					Места работы прежних					Новые места
варианта				(НС)			сотрудников (ПМ)						(НМ)
1				3, 4, 7, 8				1, 2, 3				1, 2

2				1, 2, 5, 6				2, 5, 6				2, 3

3				5, 6, 7, 8				1, 2, 5				3, 4

4				3, 4, 5, 6				4, 5, 6				1, 4

5				1, 2, 3, 4				2, 3, 4				2, 4

6				2, 4, 6, 8				3, 4, 6				1, 3

7				1, 3, 5, 7				2, 3, 6				1, 4

8				2, 3, 6, 7				3, 4, 5				2, 3

9				1, 4, 5, 8				2, 3, 5				3, 4

10				2, 3, 4, 5				1, 2, 6				1, 2

11				4, 5, 6, 7				1, 3, 5				2, 4
12				1, 2, 7, 8				2, 4, 6				1, 3

Таблица 13 - Компетентность новых сотрудников
	НМ1		НМ2		НМ3	НМ4	ПМ1	ПМ2	ПМ3		ПМ4		ПМ5	ПМ6
НС1	6		5		7	6	5	6		7	6		7	5
НС2	5		5		8	8	7	6		4	5		8	8
НС3	6		7		5	6	4	5		4	5		6	6
НС4	7		8		7	6	5	7		6	8		5	5
НС5	7		6		6	5	5	4		5	5		4	6
НС6	8		8		9	7	6	7		8	7		9	8
НС7	9		8		9	9	8	7		8	9		8	7
НС8	7		7		8	9	7	8		9	6		7	8

Таблица 14 - Компетентность прежних сотрудников

	НМ1	НМ2	НМ3	НМ4
ПС1	7	6	6	7
ПС2	8	9	7	7
ПС3	6	5	6	6
ПС4	7	9	6	8
ПС5	8	7	8	8
ПС6	4	5	6	4

Рекомендации к решению задачи

1. Процесс приведения задачи о назначениях к закрытому виду имеет свои особенности по сравнению с транспортной задачей. Если условие сбалансированности задачи (18) не выполняется из-за нехватки работ или

исполнителей в количестве kab , то для создания баланса надо ввести такое же количество kab фиктивных работ или исполнителей.

2.Особенностью решения данной задачи является моделирование системы предпочтений, сложившейся у руководства предприятия по описанному в условии задачи кадровому вопросу.

3.В задаче о назначениях увольнение прежнего сотрудника или непринятие на работу нового сотрудника моделируется попаданием единицы

вфиктивный столбец матрицы решений задачи, поэтому для запрещения или разрешения таких ситуаций необходимо использовать соответствующие "тарифы".

4.Значения "тарифов" cij3 выбираются в зависимости от направления

оптимизации	целевой функции	задачи о назначениях ( F (X ) → max или
F (X ) → min ).	При этом руководствуются принципом "невыгодности"
запрещенных	назначений. Так,	если F (X ) – это общая компетентность

работников, то в качестве запрещающих надо выбирать нулевые компетентности cij3 .

Контрольные вопросы

1.Какова постановка задачи о назначениях?

2.В чем отличие модели задачи о назначениях от модели транспортной задачи?

3.Каковы исходные и искомые параметры задачи о назначениях?

4.Объяснить построение математической модели задачи о назначениях.

5.Какие переменные называются булевыми?

6.Как решается задача с булевыми переменными в Excel?

Лабораторная работа № 9 Численные методы решения задач нелинейного программирования

Цель работы: Приобретение навыков решения задач нелинейного программирования в табличном процессоре Excel.

Задача нелинейного программирования формулируется так же,

как и общая задача линейного программирования, то есть в виде (22) - (24), со следующими требованиями к целевой функции и области

допустимых решений: целевая функция F(X ) = f (x1 , x2 ,..., xn ) или (и)


			ϕi (x1 , x2 ,..., xn ) ( i =				)
хотя	бы одна из	функций	ϕi (x1 , x2 ,..., xn ) ( i =			1,m	)	являются
нелинейными:		max(min) f (x1 , x2 ,..., xn ),
		max(min) f (x1 , x2 ,..., xn ),						(22)
		ϕ i (x1 , x2 ,..., xn ) {£, =, ³}bi , i =			,
		ϕ i (x1 , x2 ,..., xn ) {£, =, ³}bi , i =		1, m	,			(23)
		x j	³ 0, j = 1,..., n.					(24)
Для задач линейного программирования характерно следующее:
∙	Множество допустимых решений выпукло.
·	Множество	всех точек (x1, x2 ,..., xn ) n-мерного пространства, в

которых целевая функция принимает заданное значение, есть линия уровня. Линии уровня, соответствующие разным значениям целевой функции, параллельны.

·Локальный максимум (минимум) является также глобальным максимумом (минимумом) целевой функции.

·Если оптимальное значение целевой функции ограничено, то по крайней мере одна угловая точка области допустимых решений является оптимальным решением.

У произвольной задачи нелинейного программирования некоторые или все приведенные выше свойства ЗЛП отсутствуют. Вследствие этого задачи нелинейного программирования намного сложнее задач ЛП и для них не существует общего универсального метода решения. Задачи нелинейного программирования, за малым исключением, поддаются лишь численным методам решения.

Применение численных методов для отыскания точек локального

максимума (минимума) функции f (x) предполагает:

1)определение промежутков унимодальности функции, то есть нахождение отрезков, которым принадлежит одна точка локального максимума (минимума).

2)вычисление значения x* , принадлежащего выбранному отрезку, с заданной точностью ε .

Метод половинного деления

Пусть при решении задачи

f (x) → min

определен отрезок [а, b], которому принадлежит точка локального минимума x* и функция f (x) является унимодальной на этом отрезке.

Для сужения отрезка унимодальности [а, b] используем точки x1 и x2 , расположенные симметрично относительно середины отрезка [а, b]:

x2,1	=	a + b	± k	b − a	, k << 1.

	2		2

Поскольку k гораздо меньше 1, точки x1 и x2 принадлежат отрезку [а, b], получим новый суженный отрезок [а1, b1], выбрав его длину в одном из трех возможных случаев:

1.	f (x ) < f (x		),	a = a ,								b = x						=			a + b		+ k	b − a	.
1.	f (x ) < f (x	2	),	a = a ,								b = x				2		=					+ k		.
	1	2			1						1					2		2				2
										a + b			b − a					2				2
2.	f (x ) > f (x		),	a		= x =				a + b		− k	b − a				,						b = b .
2.	f (x ) > f (x	2	),	a	1	= x =						− k					,						b = b .
	1	2			1		1			2				2								1
	f (x1 ) = f (x2 ),			a1 = x1 ,						2				2								b1 = x2 .
3.	f (x1 ) = f (x2 ),			a1 = x1 ,																		b1 = x2 .
	В новом суженном промежутке [а1, b1]																	выберем точки x1,1 и x2,1 ,
симметричные относительно его середины:
					x =			a1 + b1				− k		b1 − a1						,
					x =							− k								,
						1,1				2				2
										2				2
						x2,1	=		a1 + b1			+ k			b1 − a1				.
						x2,1	=					+ k							.
										2				2

Проведя вычисления функции, устанавливаем отрезок [а2, b2]. Далее продолжаем итерационные вычисления до тех пор, пока не будет выполняться неравенство:

bn − an ≤ ε.

В качестве приближенного значения точки минимума x* выбираем середину отрезка [an ,bn ].

Метод золотого сечения

Точка x1

является золотым сечением отрезка [а, b], если отношение

длины всего отрезка

b − a

к длине большей части

b − x1

равно отношению

длины большей части отрезка к длине

x1 − a

меньшей части. То есть точка

x1 является золотым сечением, если справедливо отношение:

b − a

b − x1

(25)

b − x1

x1 − a

Аналогично, точка x2 , симметричная точке x1 относительно середины

отрезка [а, b],

является вторым золотым сечением этого отрезка. Так как

точки x1 и x2

расположены симметрично относительно середины отрезка

[а,b], то можно записать:

x	=	a + b	±	b − a	.	(26)

1,2	2		2

Учитывая, что

b − x1 = (1 + k ) b − a , 2

x1 − a = (1 − k ) b − a , 2

и используя определение золотого сечения (23), можно вычислить, что число k = 5 − 2.

Алгоритм метода

На исходном отрезке [а, b] по формуле (24) при k =

− 2

находятся

точки

, а затем разность

x = x − x .

Вычисляются значения функции y1 = f (x1 ),

= f (x2 ), определяется

суженный отрезок [а1, b1], находятся сечения

x11

x12 .

При

этом

возможны три случая:

b = x , x1 = x

y < y

a = a ,

= a +

;

> y

a = x ,

b = b ,

= x

x1 = b −

x ;

3) y1 = y 2 ,

a1 = x1 ,

b1 = x2 ,

x11,2 =

a + b

± k

b − a

Определяются отрезки [а2, b2], [а3, b3] и т.д..

≈ a

≈ b

Точность

приближенного

равенства

на

n-м

шаге

вычислений можно оценить неравенством:

−1

b − a

< ε

Реализация алгоритма в Excel

Рассмотрим реализацию метода в Excel на примере нахождения

локального

минимума

функции

f (x) = 2x2 − ln x

на отрезке [0,25;

1] с

точностью ε =0,1.

Введем в ячейку В2 формулу для вычисления величины k, в ячейку С2

– левую границу отрезка а, в ячейку D2 –

правую границу b, в ячейки Е2 и F2

- формулы для вычисления соответственно

x2 ,

а в ячейки G2 и Н2 -

выражения функции y1

и y2 через адреса ячеек x1 и x2 (таблица 15).

Таблица 15 – Формулы для реализации метода золотого сечения

Объект

Формула Excel

=5^0,5-2

=(C2+D2)/2-$B$2*(D2-C2)/2

=(C2+D2)/2+$B$2*(D2-C2)/2

=2*E2^2-LN(E2)

=2*F2^2-LN(F2)

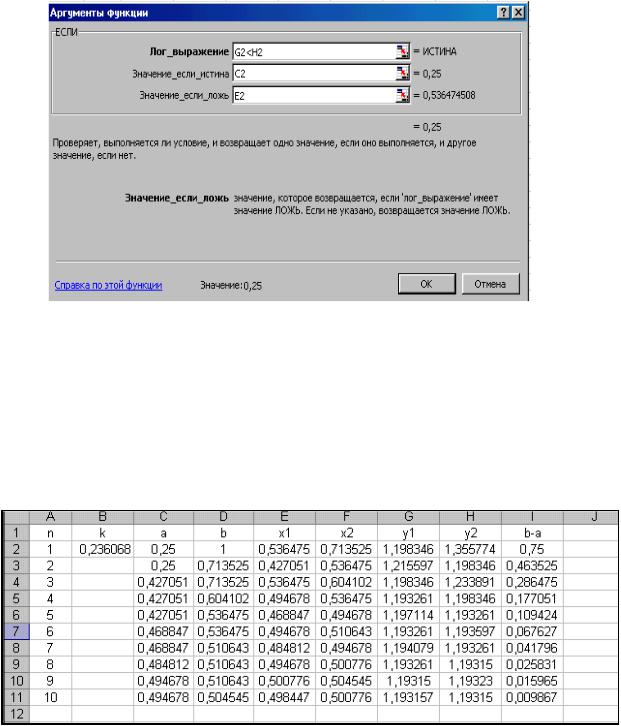
Дальнейшее сужение интервала [а, b] производится с помощью функции ЕСЛИ (рисунок 26). В ячейки С3 и D3 вводим функцию ЕСЛИ с соответствующими условиями:

=ЕСЛИ (G3<H3; C3;E3)

=ЕСЛИ (G3<H3; F3;D3)

Рисунок 26 – Диалоговое окно функции ЕСЛИ

Ячейки F2, G2, Н2 надо выделить и скопировать формулы в ячейки F3, G3, H3. Затем выделяем строку 3 и копируем формулы в другие строки, до требуемой точности расчетов. Установленная нами точность ε =0,1 достигается после пятой итерации (рисунок 27). В качестве

приближенного значения точки минимума x* выберем середину этого отрезка: x* = 0,50266.

Рисунок 28 – Результаты минимизации функции методом золотого сечения

Выделив ряды а, b, x1 , x2 и построив график (рисунок 29), можно получить графическое решение задачи.

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
04.06.2015348.32 Кб12%ed%c5%d4%cf%c4%c9%de%cb%c1%20%f3%fc_2013.rtf
#
04.06.20151.6 Mб4505 Теплопередача - лабораторный практикум.doc
#
04.06.20152.45 Mб25907 РГР Техническая термодинамика.doc
#
04.06.20151.74 Mб7408-МУ к лаб_занятиям.pdf
#
04.06.2015102.4 Кб231 5 Отчет по лабам метрологии.doc
#
04.06.2015101.89 Кб331 5 Отчет по лабам метрологии.doc
#
27.03.201669.12 Кб141 Общая характеристика производственного объекта.doc
#
04.06.2015793.6 Кб411 СБ.ЗАДАЧ Математика 2 сем 2014.doc
#
04.06.201554.78 Кб411. Математика Содержание 1 сем 2013.doc