Образец экзаменационного билета
Часть 1 (на оценку 3). Засчитывается правильный выбор ответа из предложенных справа в таблице, но только при наличии решения.
|
Задание |
Варианты ответов | ||
|
1.
|
а) в)
| ||
|
2.
|
а)
а)
в)
| ||
|
3.
|
а)
| ||
|
4.
|
а)
б) | ||
|
5.
Найти площадь между кривой
|
а)
| ||
|
6. Найти массу области D, ограниченной линиямих=у2,х=0,у=1, если плотность масс в каждой ее точке равна(х,у) =у– 2х |
а)0,04
б) 0,1 в) | ||
|
7.
Найти работу силы F= (x, –y)
при перемещении точки вдоль четверти
эллипса |
а)
2 б)
| ||
|
8.
Найти
|
а)
| ||
|
9.Найти
направление наискорейшего возрастания
функции
|
а)
2 в)
3 | ||
|
10. Определение интегральной суммы для функции g(t) на отрезке [; ]. 11. Дайте определение максимума функции двух переменных. Сформулируйте достаточное условие максимума. 12. Дать определение двойного интеграла. 13. Перечислите свойства неопределенного интеграла. | |||
б) –
г)
б)
г) 
б)
в)
г) –
в)ln(ln2)
г)
и отрезком
оси ОХ.
б)
в)
г)
г)
в) –
г) –
,
если
,
А(1,0)
б)–1,5 в)
г) –
в точке М(1,1)
–3
б) 3
+2
–2
г) 2
+3
Ответы: 1в, 2б,3в,4а,5б,6в,7в,8б,9в
Часть 2 (на оценку 4 и 5, ответ устный, не исключаются дополнительные вопросы по определениям, теоремам).
Сформулируйте и докажите свойства определенного интеграла, касающиеся отрезка интегрирования.
Сформулируйте и решите задачу о вычислении массы дуги LR3 с переменной линейной плотностью = (х, у, z).
Какой из интегралов больше :
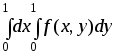или
,
если f(x,y)
>0?Докажите, что две первообразные для заданной функции отличаются только константой.