Вариант 5

1. Бросают три монеты. Вероятность выпадения герба при одном бросании равна 0,5. Составьте закон распределения случайной величины Х – числа выпавших гербов.

2. Найти вероятность 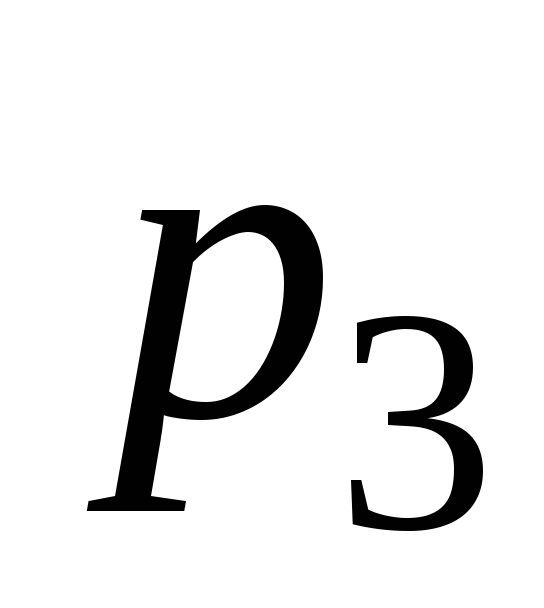,,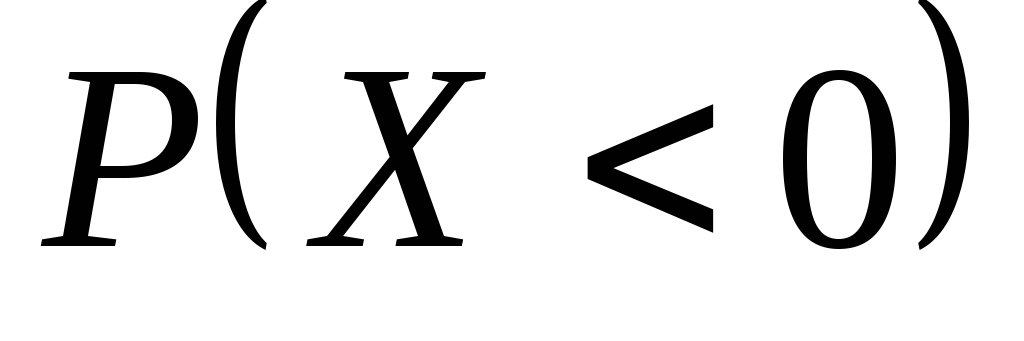 математическое ожидание и дисперсию дискретной случайной величиныХ, заданной рядом распределения:

Х	-2	-1	0	1	2
P	0,2	0,1		0,2	0,1

3. Непрерывная случайная величина Х задана интегральной функцией распределения: 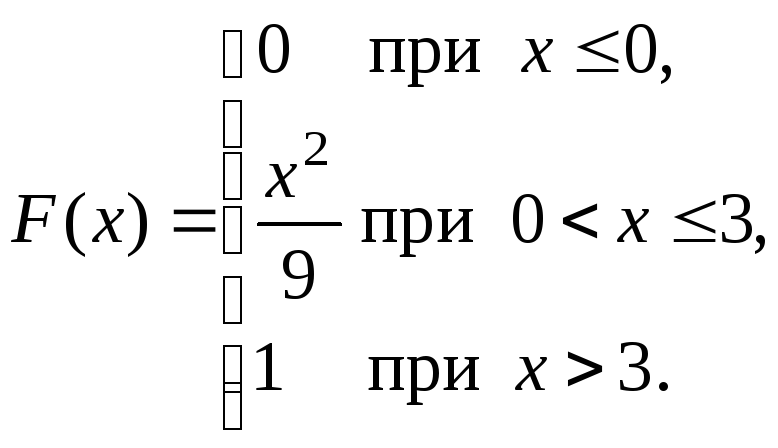Найти математическое ожидание и дисперсию случайной величиныХ, а также вероятность того, что значения случайной величины Х попадут в интервал (1; 2).

4. Непрерывная случайная величина Х имеет плотность распределения 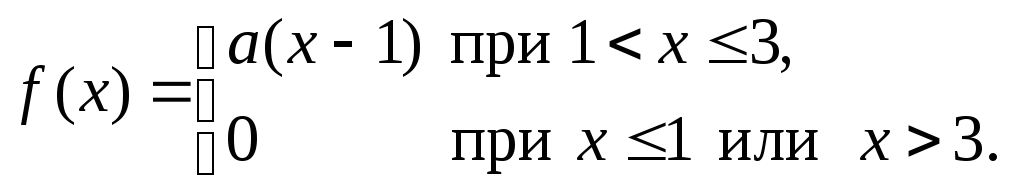Найти значение параметраа и .

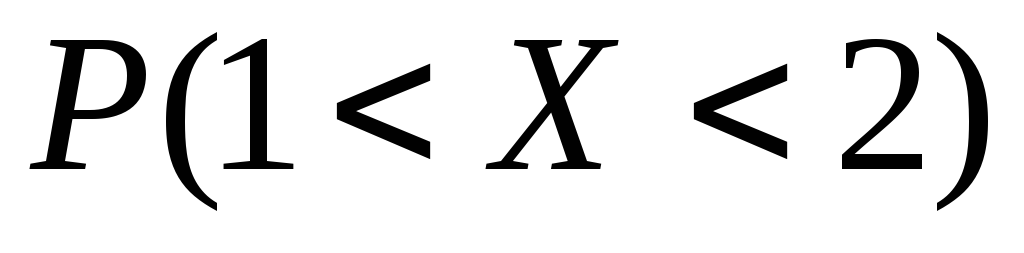5. Функция распределения равномерно распределенной случайной величины Х имеет вид: 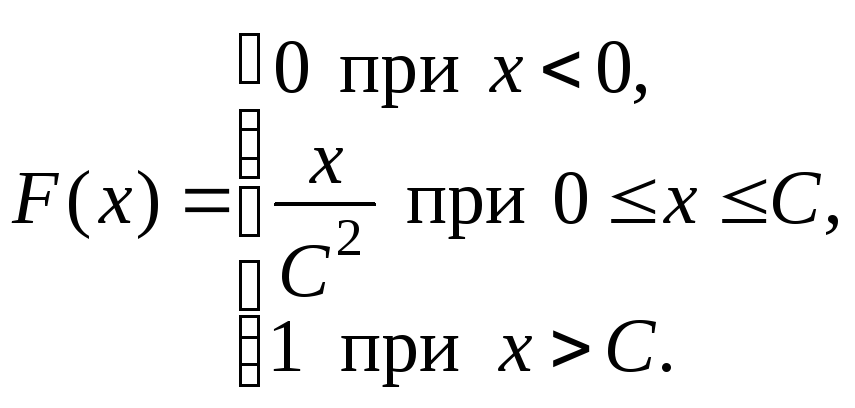Найти значение константыС, функцию плотности вероятности f(x), М(х), D(x), построить графики функций f(x) и F(x).

6. Случайная величина Х распределена по нормальному закону: 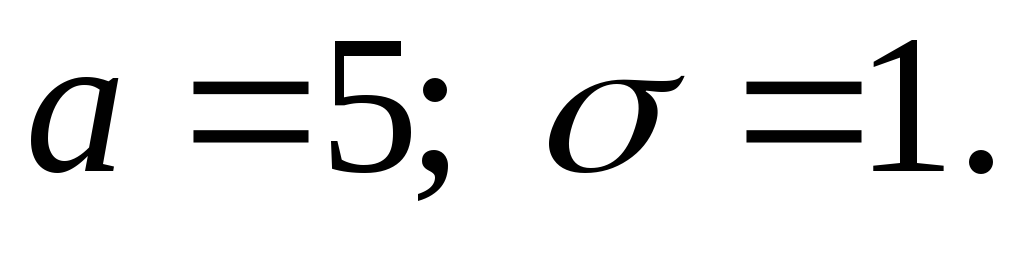Найти вероятность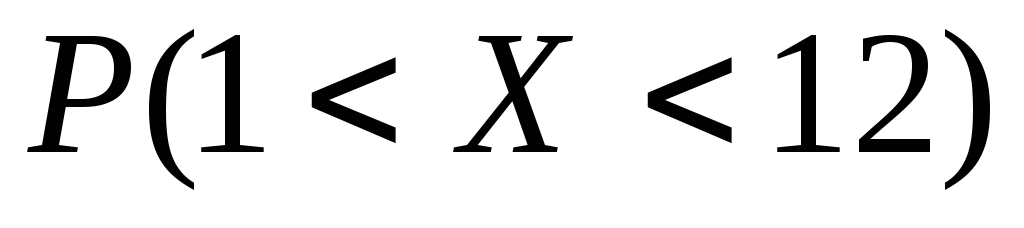. Построить схематический график функции плотности вероятностиf(x).

7. Суточная потребность электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 3000 кВт/ч, а дисперсия составляет 2500. Оценить вероятность того, что в ближайшие сутки расход электроэнергии в этом населенном пункте будет от 2500 до 3500 кВт/ч.

Вариант 6

1. В партии из 100 деталей находятся две бракованные детали. Из партии наудачу отбираются 10 деталей. Составьте закон распределения случайной величины Х – числа бракованных деталей среди отобранных.

2. Найти вероятности 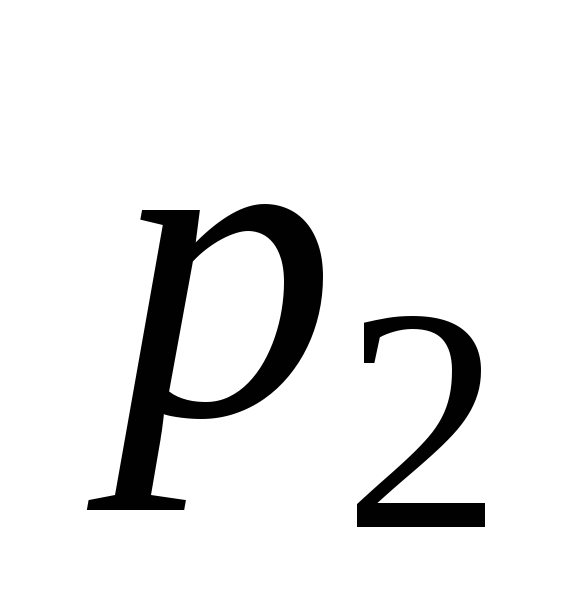,,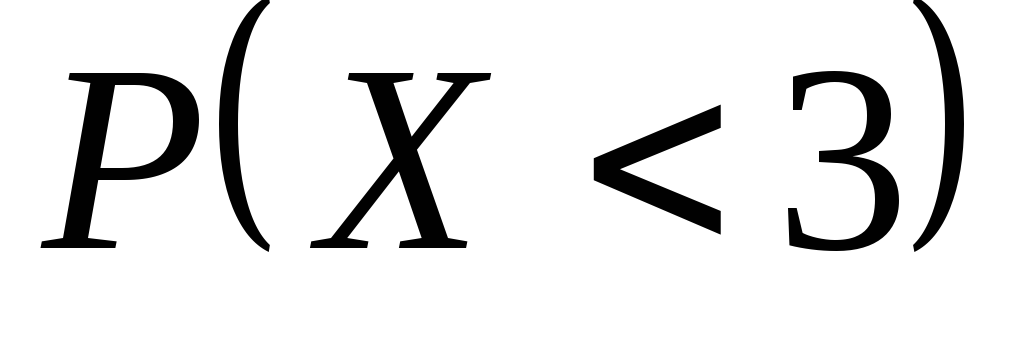 математическое ожидание и дисперсию дискретной случайной величиныХ, заданной рядом распределения:

Х	0	1	2	3	4
P	0,05		0,3	0,35	0,1

3. Непрерывная случайная величина Х задана интегральной функцией распределения: 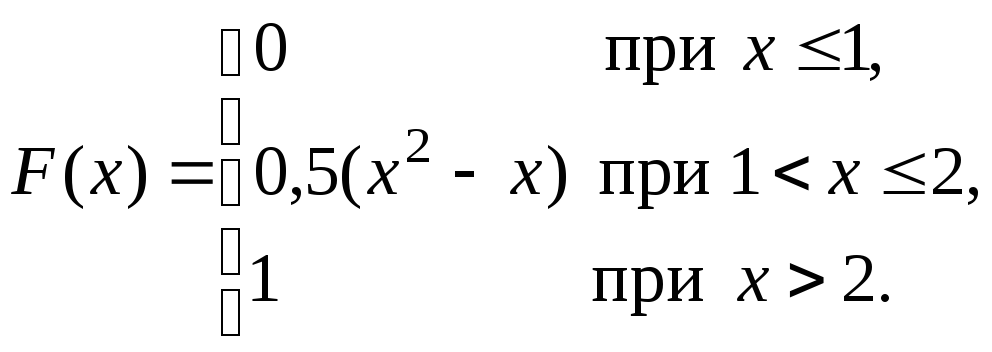Найти математическое ожидание, дисперсию заданной случайной величиныХ и вероятность .

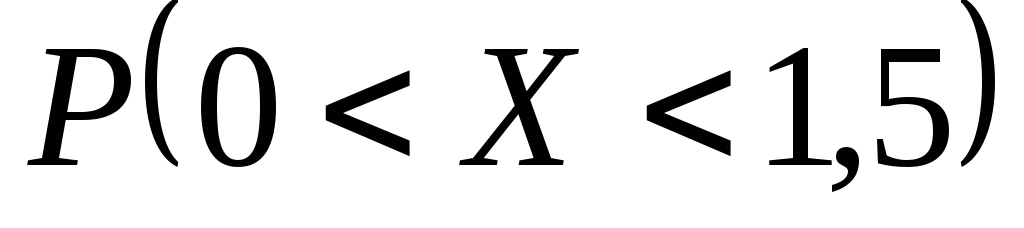4. Непрерывная случайная величина имеет плотность вероятности 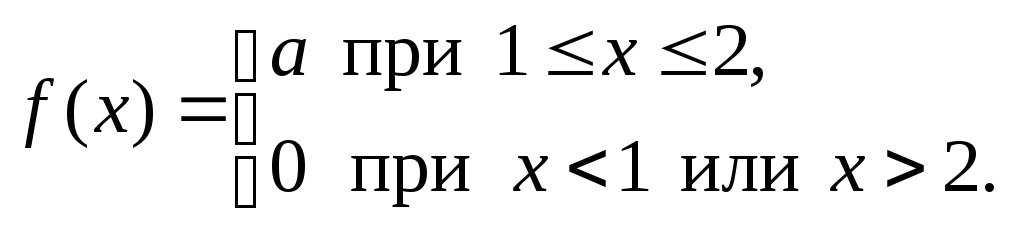Найти значение параметраa, функцию распределения 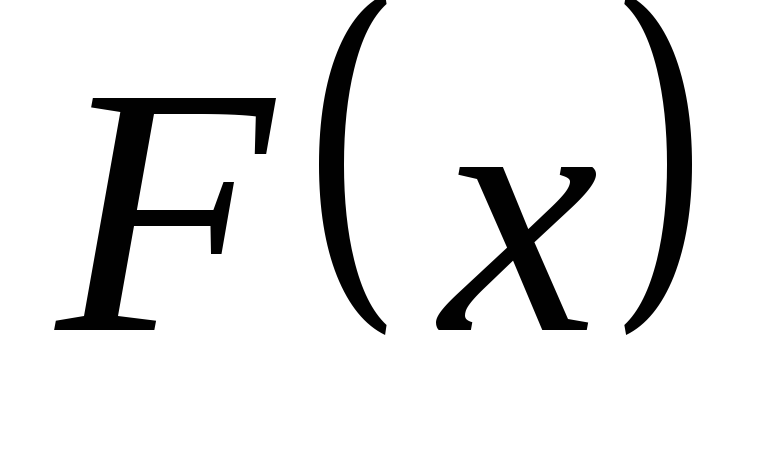и вероятность.

5. Непрерывная случайная величина Х равномерно распределена на отрезке [1; 5] и имеет плотность вероятности

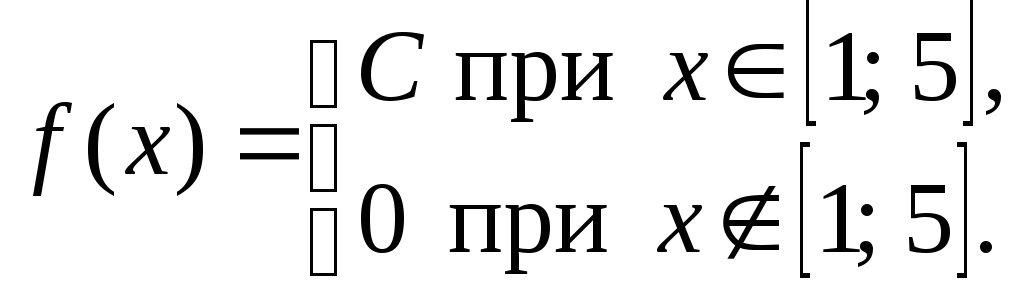
Найти значение параметра С, математическое ожидание и дисперсию, построить график функции f(x).

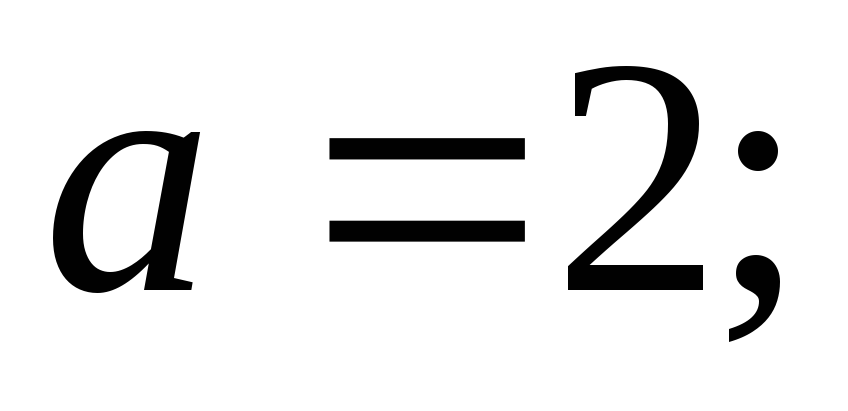
6. Случайная величина Х распределена по нормальному закону: 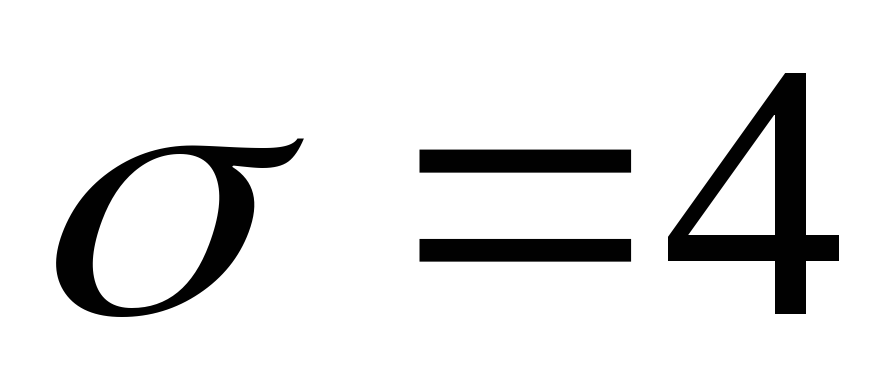. Найти 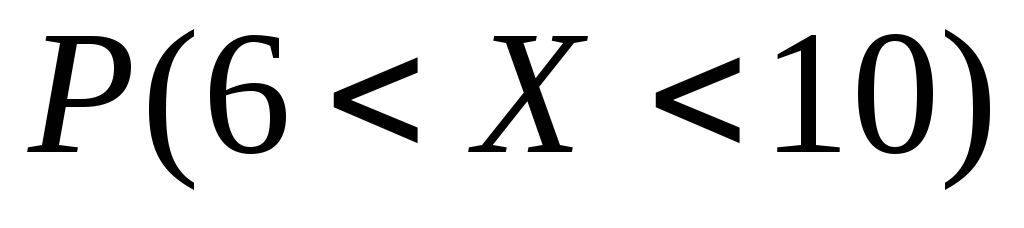, построить схематический график функции плотностиf(x).

7. Вероятность получения с конвейера изделия высшего качества равна 0,6. Используя неравенство Чебышева и интегральную теорему Лапласа, оценить вероятность наличия от 340 до 380 изделий высшего качества в партии из 600 изделий. Сравнить результаты.