
- •Типовой расчет по теме «Случайные величины» Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Образец защиты темы
Вариант 21
В билете три задачи. Вероятность правильно решить первую задачу – 0,9, для второй задачи – 0,8, для третьей – 0,7. Составить закон распределения случайной величины X – числа правильно решенных задач.
Найти вероятности
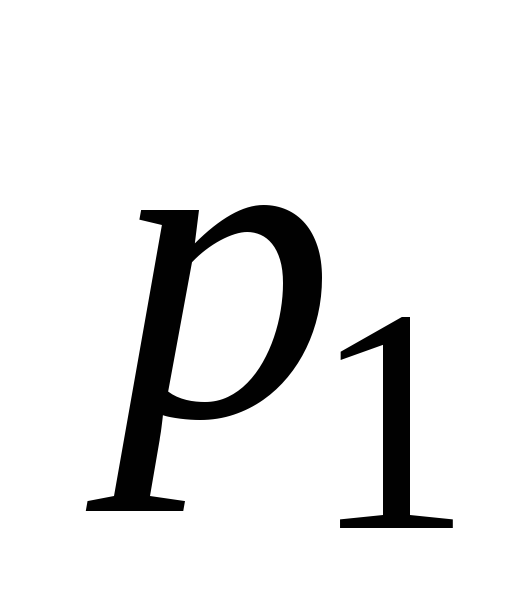 и
и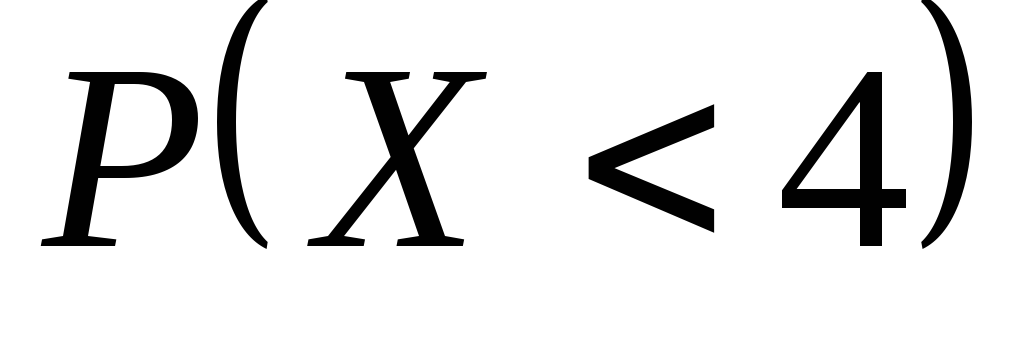 ,
математическое ожидание и дисперсию
дискретной случайной величиныХ,
заданной законом распределения:
,
математическое ожидание и дисперсию
дискретной случайной величиныХ,
заданной законом распределения:
|
Х |
0 |
2 |
4 |
6 |
|
P |
|
0,2 |
0,25 |
0,15 |
Непрерывная случайная величина Х задана интегральной функцией распределения:
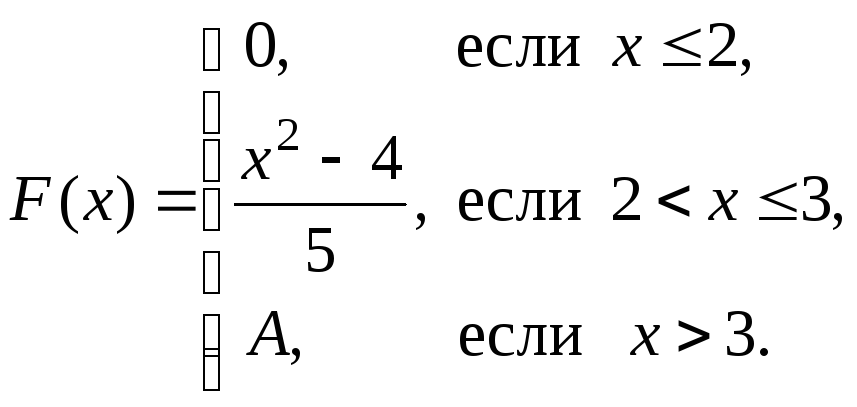 Найти значение параметраA,
математическое ожидание и дисперсию,
вероятность
Найти значение параметраA,
математическое ожидание и дисперсию,
вероятность
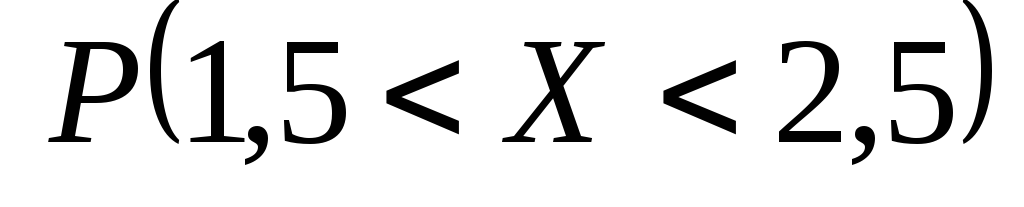 .
.
Случайная величина Х имеет плотность вероятности
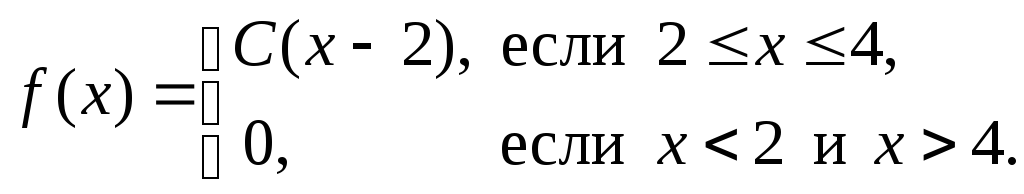 Найти значение параметраС,
математическое ожидание и вероятность
Найти значение параметраС,
математическое ожидание и вероятность
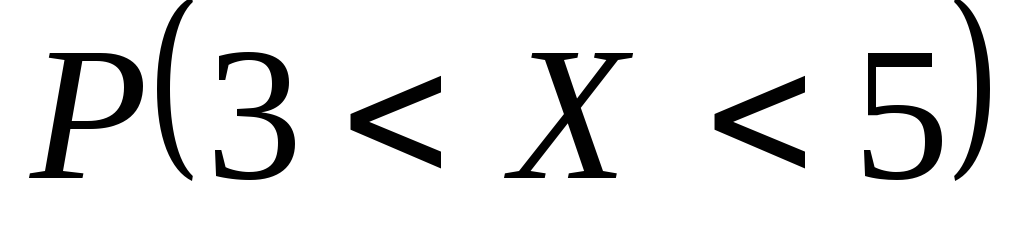 .
.
Случайная величина распределена по нормальному закону, математическое ожидание и среднее квадратическое отклонение для которого равны соответственно 5 и 1. Построить кривую распределения. Найти интервал, в который попадет случайная величина Х с практической достоверностью (вероятностью 0,9973).
Случайная величина Х имеет равномерное распределение с математическим ожиданием, равным 2 и дисперсией, равной 4/3. Записать функцию плотности вероятности f(x), функцию распределения F(x), построить их графики. Найти вероятность попадания случайной величины Х в интервал
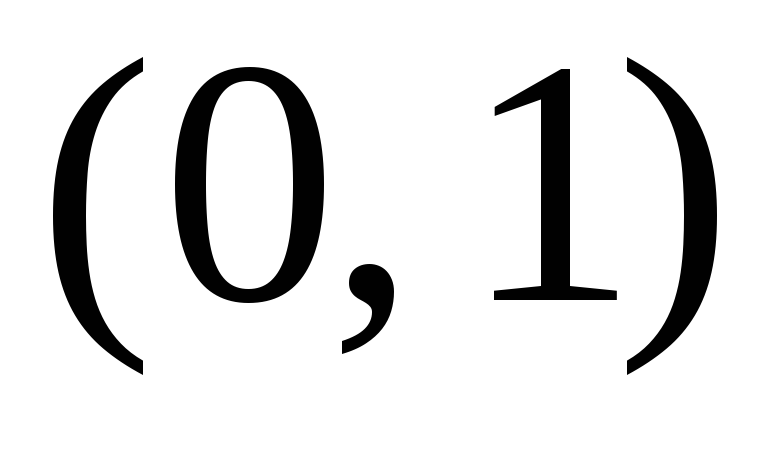 .
.
Оценить вероятность того, что при 3600 подбрасываниях игрального кубика шесть очков появится более 900 раз.
Вариант 22
В магазине 4 импортных и 2 отечественных микроволновых печи. Составить закон распределения случайной величины X – числа импортных печей среди 3 отобранных.
Найти вероятности
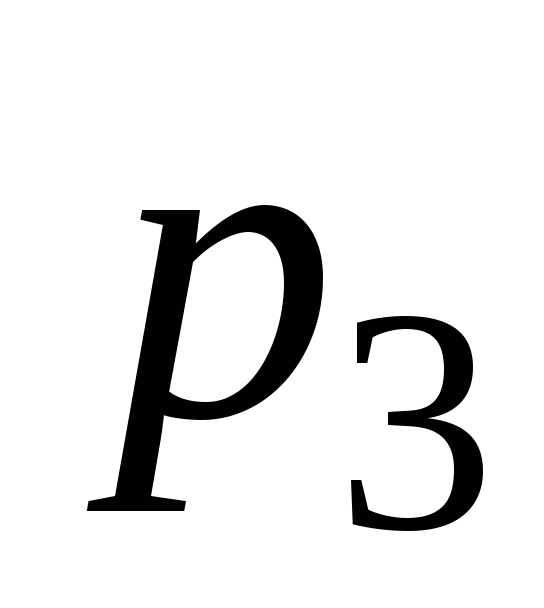 и
и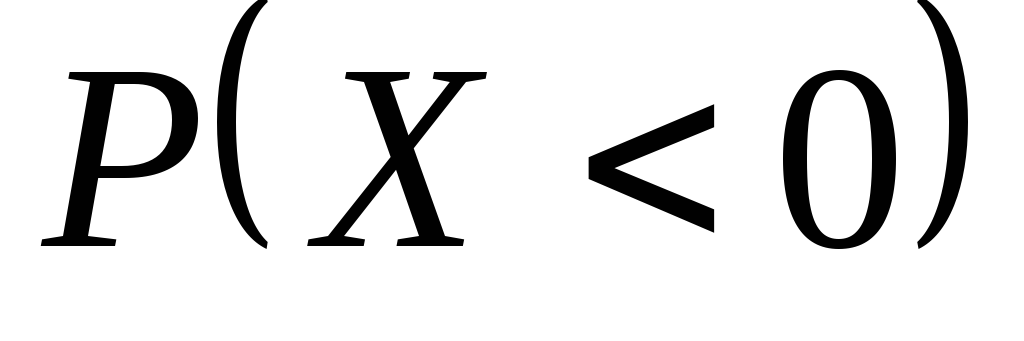 ,
математическое ожидание и дисперсию
дискретной случайной величиныХ,
заданной законом распределения:
,
математическое ожидание и дисперсию
дискретной случайной величиныХ,
заданной законом распределения:
|
Х |
-3 |
-2 |
-1 |
0 |
1 |
|
P |
0,1 |
0,2 |
|
0,3 |
0,25 |
Непрерывная случайная величина Х задана интегральной функцией распределения:
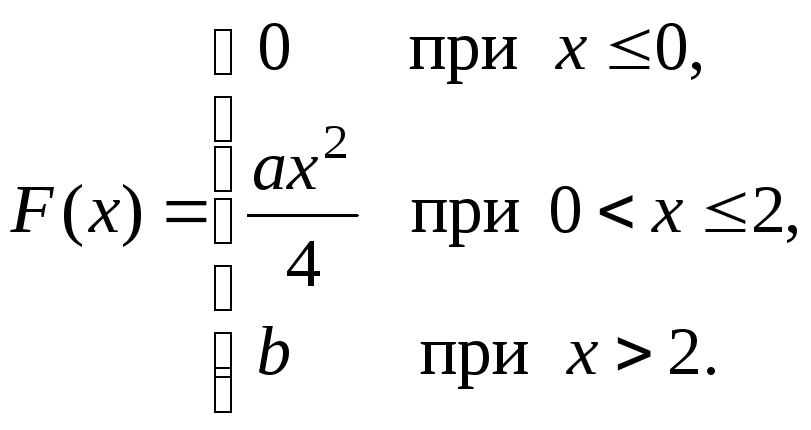 Найти значения параметрова,
b,
математическое ожидание, дисперсию и
вероятность
Найти значения параметрова,
b,
математическое ожидание, дисперсию и
вероятность
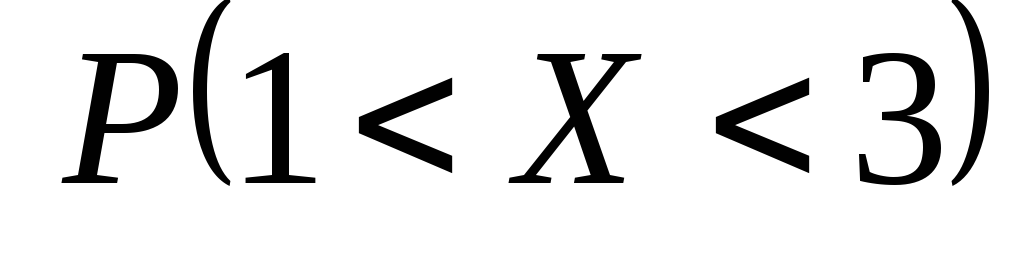 .
.
Случайная величина Х имеет плотность вероятности
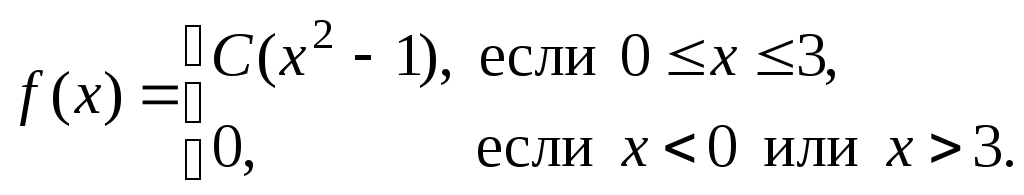 Найти значение параметраС,
математическое ожидание, вероятность
Найти значение параметраС,
математическое ожидание, вероятность
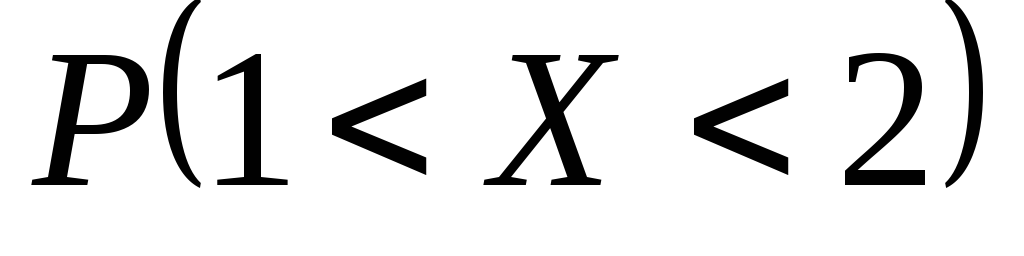 .
.
Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10; 50). Сделать схематический чертеж функции плотности вероятности f(x).
Случайная величина Х равномерно распределена на интервале
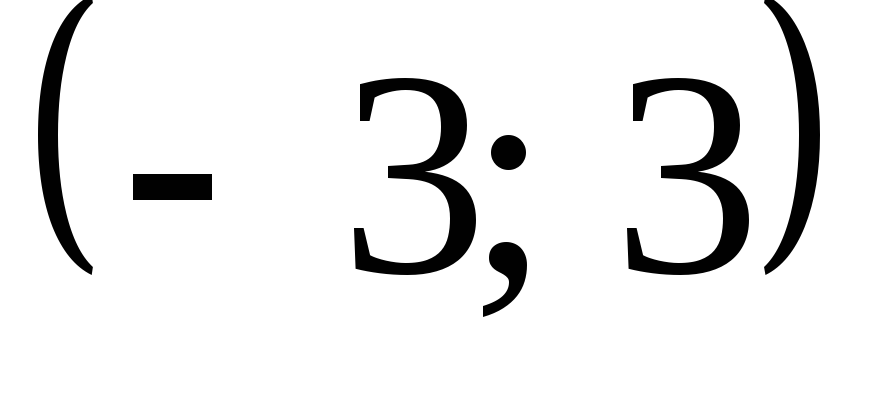 .
Записать функцию плотности вероятности f(x),
функцию распределения F(x),
построить их графики. Найти математическое
ожидание, дисперсию и вероятность
попадания случайной величины Х
в интервал
.
Записать функцию плотности вероятности f(x),
функцию распределения F(x),
построить их графики. Найти математическое
ожидание, дисперсию и вероятность
попадания случайной величины Х
в интервал
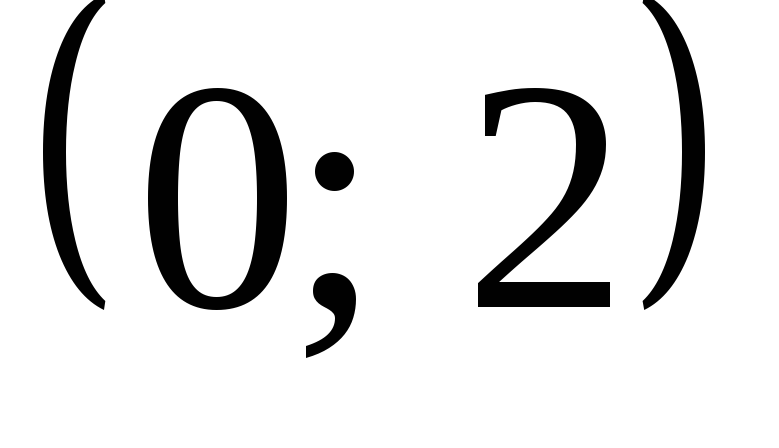 .
.Дано:
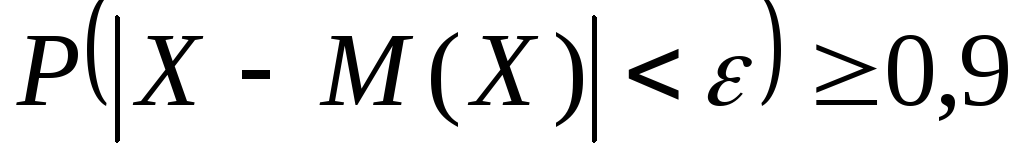 ;
дисперсия случайной величиныХ
равна 0,004. Пользуясь неравенством
Чебышева, найти
;
дисперсия случайной величиныХ
равна 0,004. Пользуясь неравенством
Чебышева, найти
 .
.
