Вариант 19

1. Устройство состоит из трех взаимно независимых элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения случайной величины X – числа отказавших элементов в одном опыте.

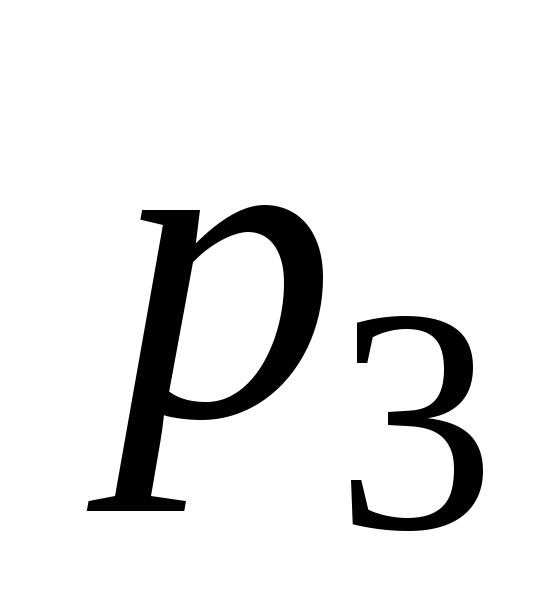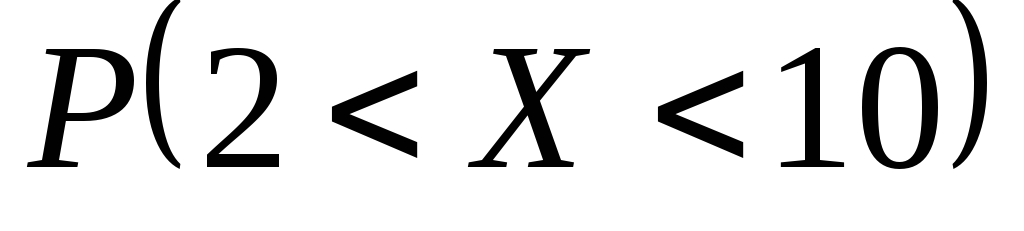2. Найти вероятности и, математическое ожидание и дисперсию дискретной случайной величиныХ, заданной законом распределения:

Х	2	4	8	10
P	0,1	0,2		0,3

3. Непрерывная случайная величина Х задана интегральной функцией распределения: 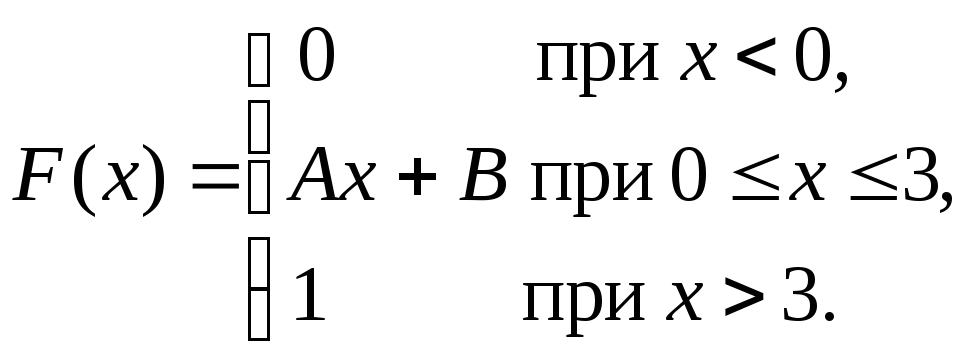Найти значение параметровA и B, вероятность 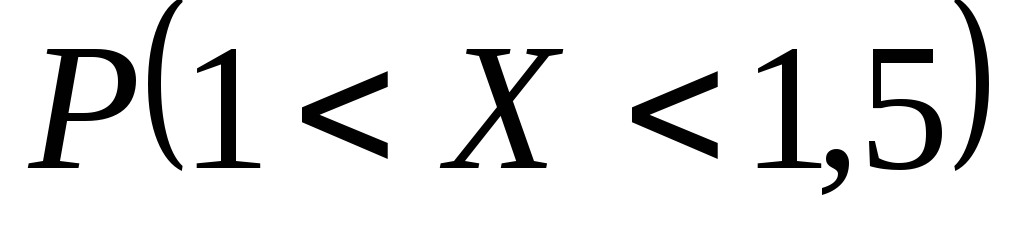и математическое ожидание случайной величиныХ.

4. Случайная величина Х имеет плотность вероятности 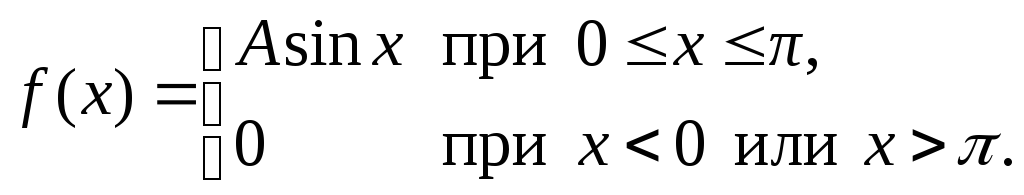Найти значение параметраА, математическое ожидание случайной величины Х и вероятность .

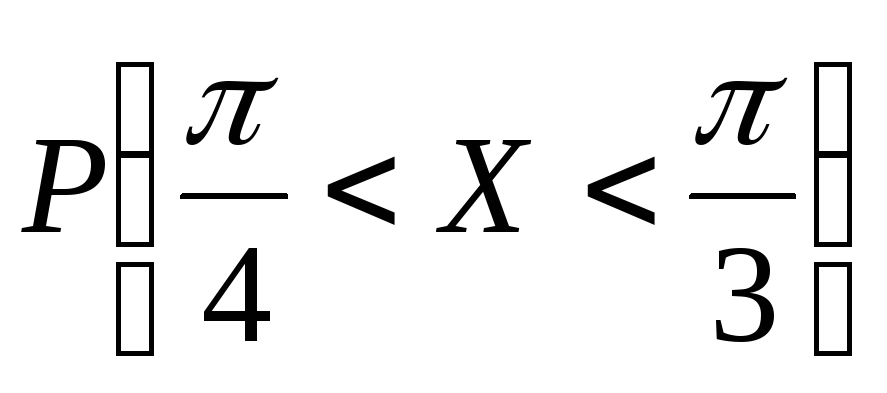5. Случайная величина распределена по нормальному закону, с математическим ожиданием, равным 5, и дисперсией, равной 4. Найти вероятность 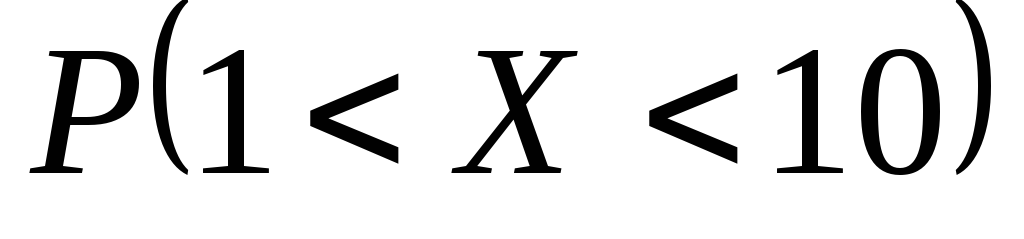. Построить схематически график функции плотности вероятности f(x).

6. Случайная величина Х равномерно распределена на интервале от -3 до 5. Записать функцию плотности вероятности f(x), функцию распределения F(x), построить их графики. Найти математическое ожидание, дисперсию и вероятность .

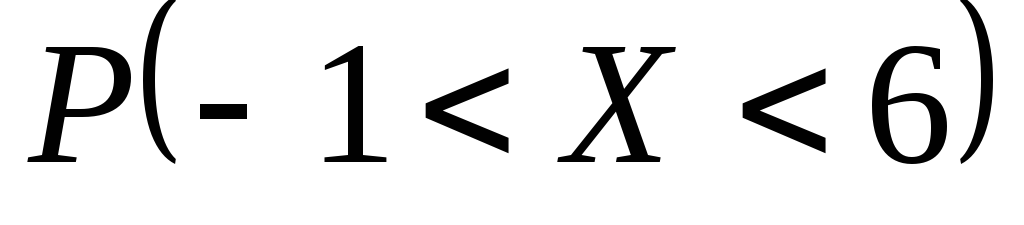7. Число солнечных дней в году для данной местности является случайной величиной Х со средним значением 100 дней и средним квадратическим отклонением 20 дней. Оценить сверху вероятность события .

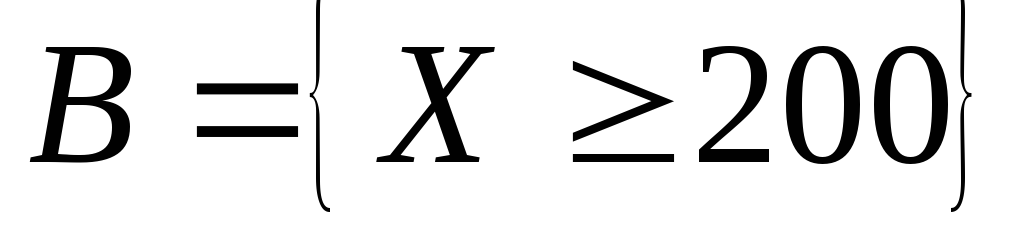Вариант 20

1. Стрелок производит по мишени 4 выстрела. Вероятность попадания при каждом выстреле 0,4. Составить закон распределения случайной величины X – числа попаданий в мишень.

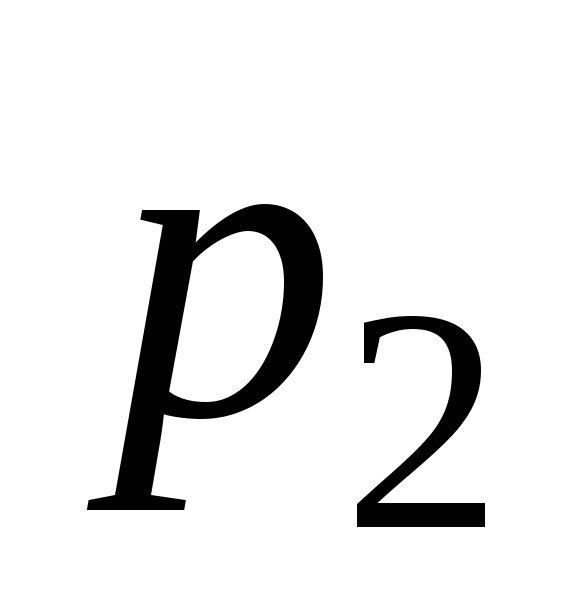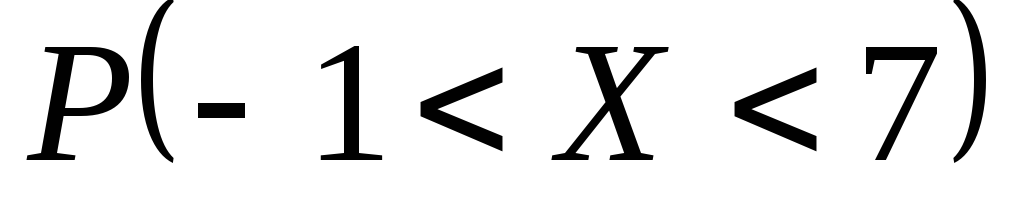2. Найти вероятности и, математическое ожидание и дисперсию дискретной случайной величиныХ, заданной законом распределения:

Х	-1	2	4	7
P	0,1		0,3	0,2

3. Непрерывная случайная величина Х задана интегральной функцией распределения: 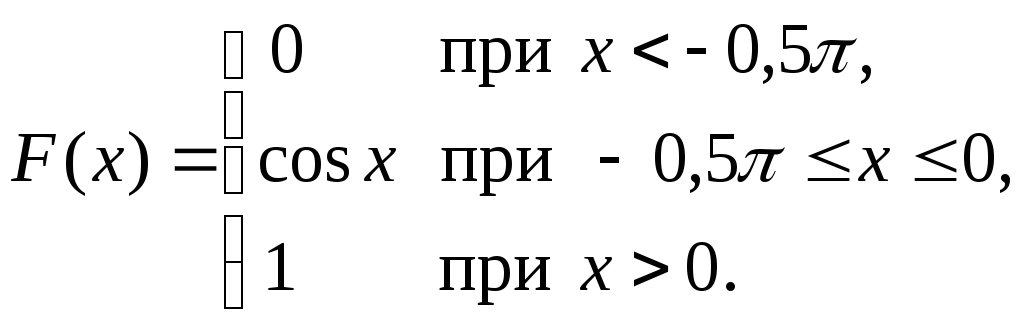Найти математическое ожидание случайной величиныХ и вероятность .

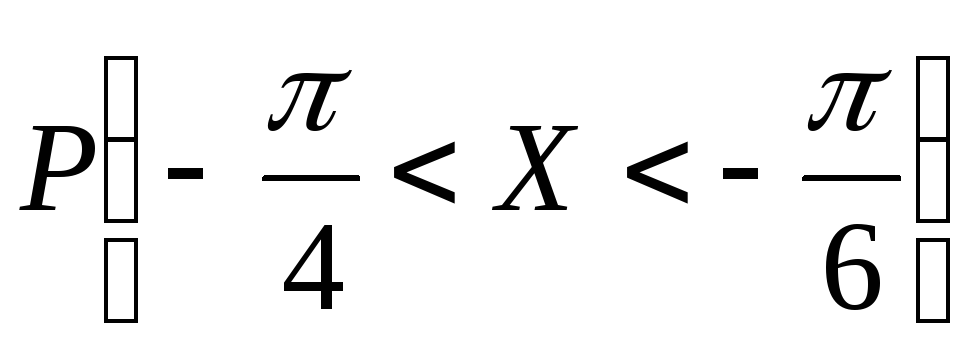4. Случайная величина Х задана функцией плотности вероятности 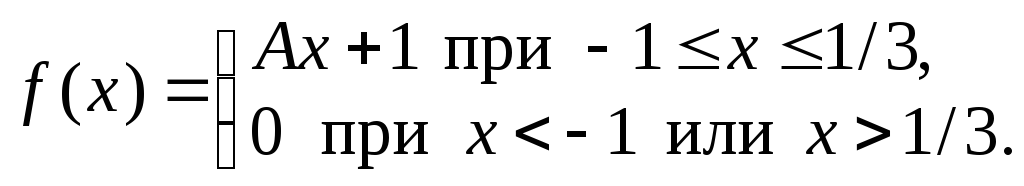Найти значение параметраA, математическое ожидание, дисперсию и вероятность .

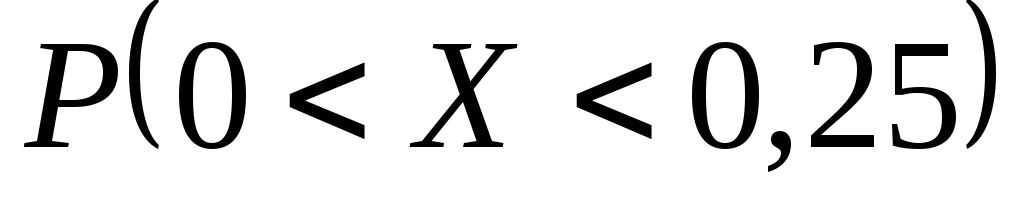5. Задана нормально распределенная случайная величина Х, математическое ожидание которой равно 5, а дисперсия – 9. Записать функцию плотности вероятности и построить схематически ее график. Найти вероятность .

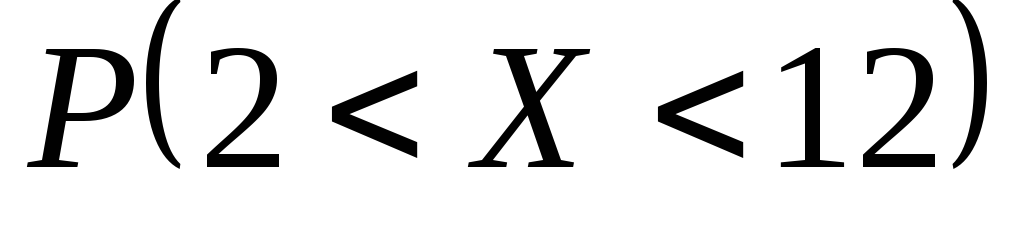6. Равномерно распределенная на отрезке [-2; 4] случайная величина Х задана функцией плотности 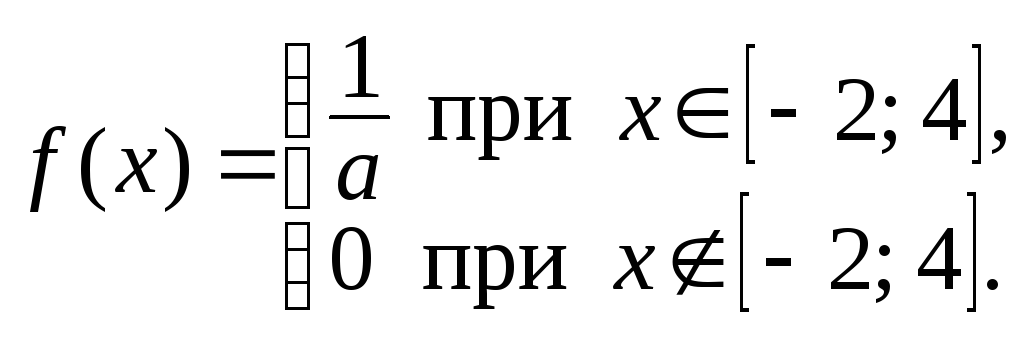Найти значение параметраа и вероятность попадания значений случайной величины Х в интервал 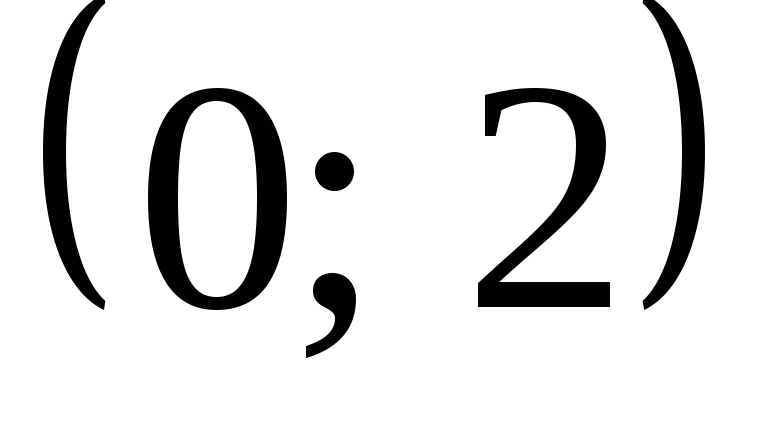, построить графики функцийf(x) и F(x). Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х.

7. Монету подбрасывают 1000 раз. Оценить вероятность отклонения частоты появления герба от вероятности появления герба при одном подбрасывании на величину, меньшую 0,1.