Типовой расчет по теме «Случайные величины» Вариант 1

1. Монету подбрасывают 4 раза. Составьте закон распределения случайной величины Х – числа выпавших гербов.

2. Найти вероятность ,,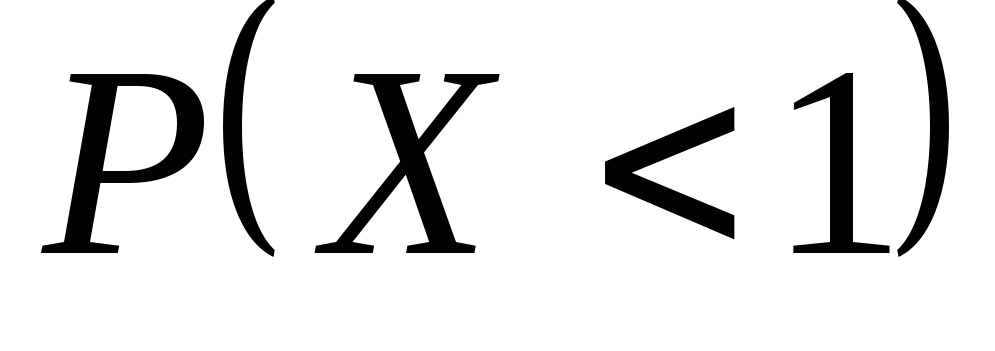 математическое ожидание и дисперсию дискретной случайной величиныХ, заданной законом распределения:

Х	-2	-1	0	1	2
P	0,1	0,2		0,3	0,1

3. Найти математическое ожидание и дисперсию случайной величины 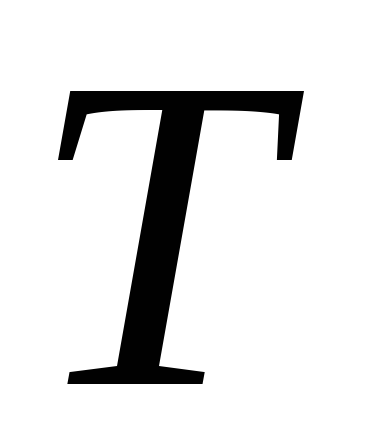– времени обслуживания, если функция распределения вероятности имеет вид:

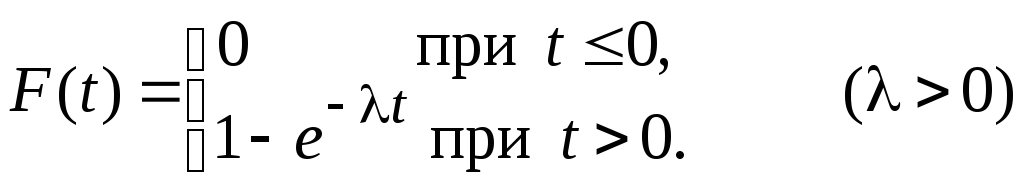
4. Непрерывная случайная величина Х задана функцией плотности вероятности 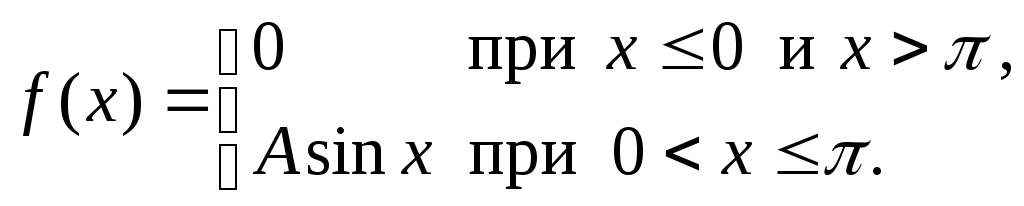Найти значение параметраА, математическое ожидание и вероятность того, что случайная величина примет значение из интервала .

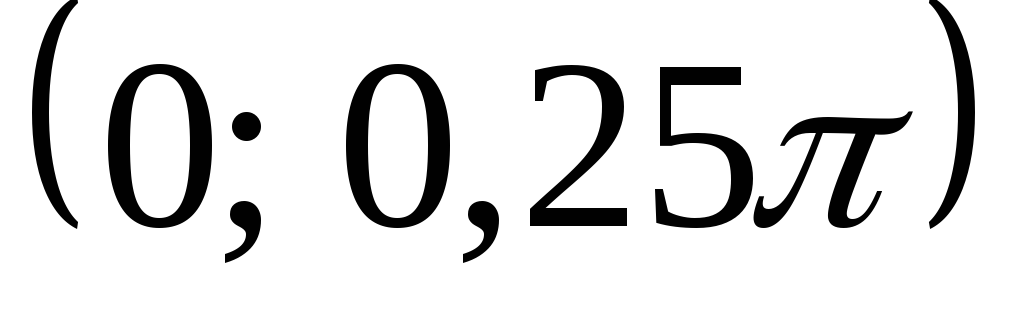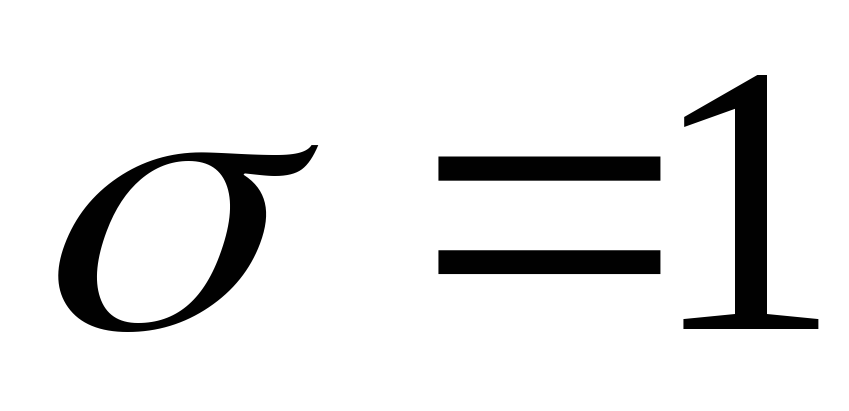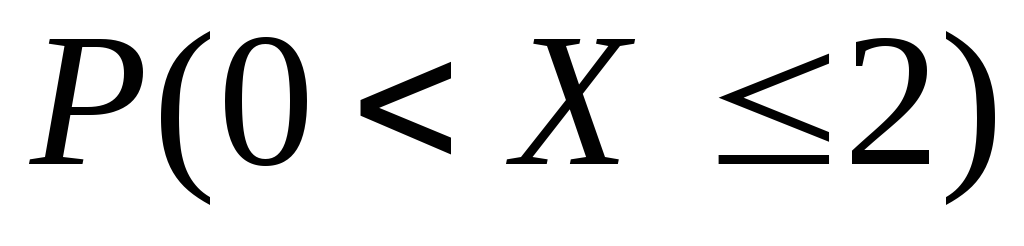5. Случайная величина Х распределена по нормальному закону: . Найти вероятность, функцию плотности распределения, построить график найденной функции.

6. Непрерывная случайная величина Х равномерно распределена на отрезке [2; 5] и имеет плотность распределения 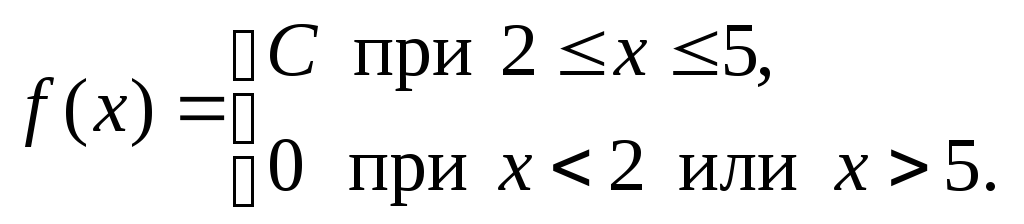Найти значение константыС, функцию распределения вероятности F(x), М(х), D(x), построить графики функций f(x) и F(x).

7. Среднее значение длины детали 50 см, а дисперсия 0,1 см. Пользуясь неравенством Чебышева, оценить вероятность того, что случайно взятая деталь окажется по длине не меньше 49,5 см и не более 50,5 см.

Вариант 2

1. Из 20 контрольных работ, среди которых 5 оценены на «отлично» наугад извлекают три работы. Составьте закон распределения случайной величины Х – числа работ, оцененных на «отлично» среди отобранных.

2. Найти вероятность ,,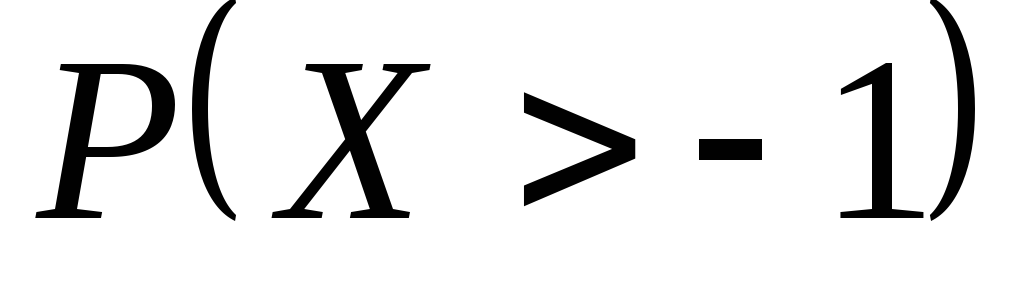 математическое ожидание и дисперсию дискретной случайной величиныХ, заданной законом распределения:

Х	-3	-2	-1	0	1
P	0,2		0,2	0,1	0,4

3. Непрерывная случайная величина Х задана интегральной функцией распределения: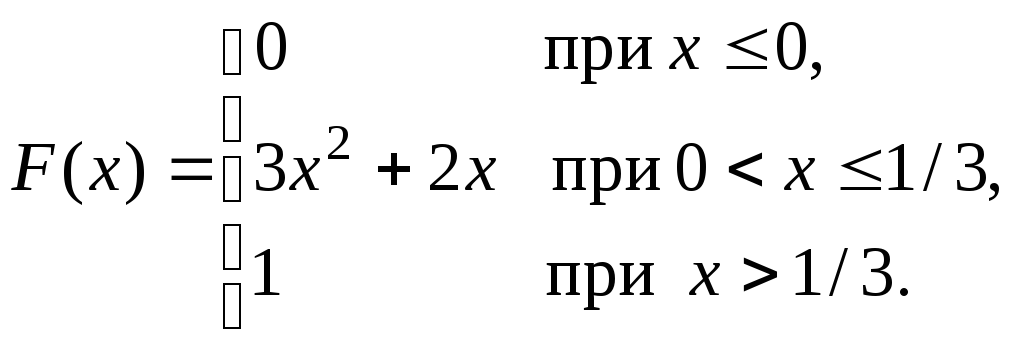Найти математическое ожидание, дисперсию случайной величиныХ и вероятность того, что её значения попадут в интервал (0,25; 1).

4. Непрерывная случайная величина Х задана функцией плотности вероятности 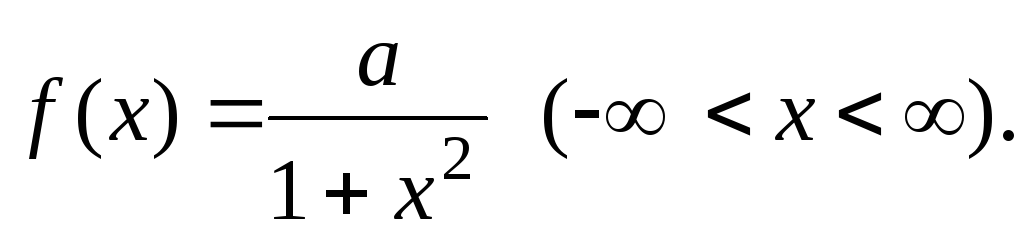Найти значение параметраа и вероятность .

5. Непрерывная случайная величина Х равномерно распределена на отрезке 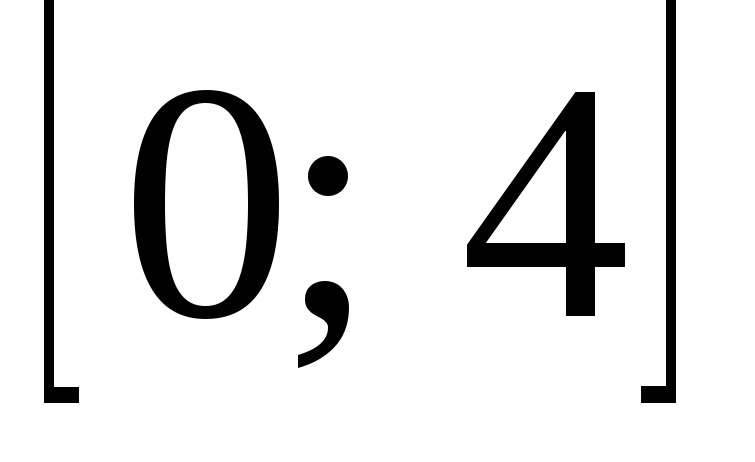, её функция плотности вероятности имеет вид:

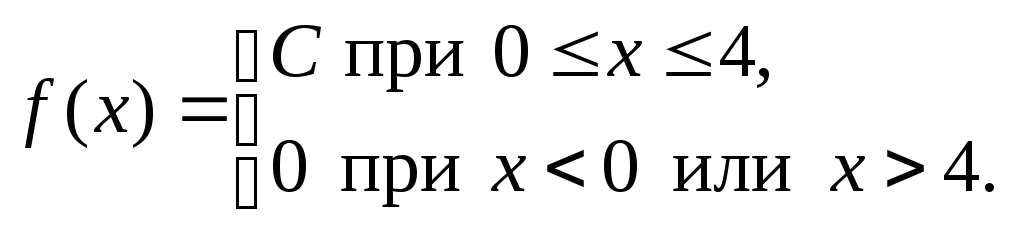
Найти значение константы С, функцию распределения вероятности F(x), М(х), D(x), построить графики функций f(x) и F(x).

6. Случайная величина Х распределена по нормальному закону: 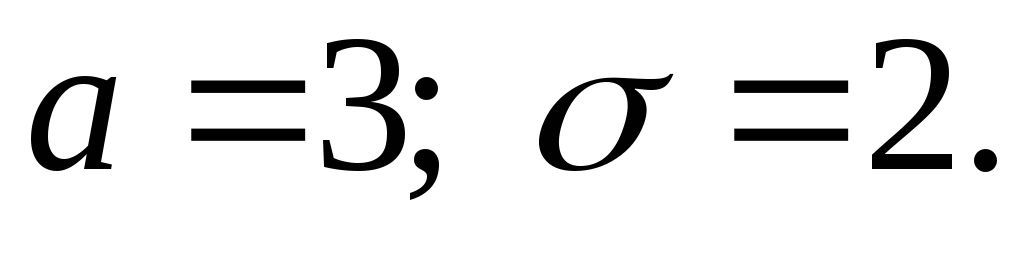Найти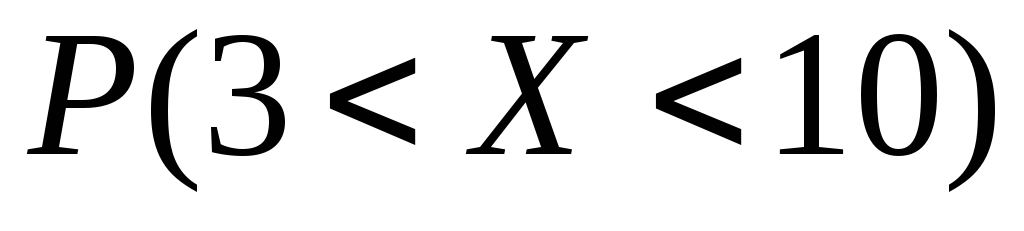. Построить схематический график функции плотности вероятности f(x).

7. Электростанция обслуживает сеть с 18000 ламп, вероятность включения каждой из которых равна 0,9. Какова вероятность того, что число включенных ламп отличается от своего математического ожидания по абсолютной величине не более чем на 200?