1.2. Уравнения с разделяющимися переменными.

Д.у. первого порядка

(1.2)

называется уравнением с разделяющимися переменными, если ив (1.2) можно записать в виде произведения двух множителей, каждый из которых является функцией одного аргумента. То есть

(1.3)

Делением на (1.3) приводится к виду

.

Интегрируя, получим общее решение д.у. в

Замечание: Если в уравнении (1.3) функция имеет действительный корень, тоявляется решением д.у.

Пример 2. Решить задачу Коши:

Решение: Полагая и вынося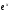за скобки, получим

.

Разделив переменные и интегрируя, находим общий интеграл

, ,.

Используя начальное условие , получим

или

Следовательно, искомое частное решение имеет вид

.

Ответ:.

1.3. Однородные уравнения.

Д.у. первого порядка называется однородным, если его можно привести к виду

(1.4)

или

, (1.5)

где и- однородные функции одного измерения, т.е. существует такое, чтои,.

Уравнения (1.4) и (1.5.) с помощью подстановки , где- новая неизвестная функция, приводятся к уравнениям с разделяющимися переменными.

Задача 3. Решить д.у. .

Решение: Разделим обе части этого уравнения на:

,

получим уравнение вида (1.4), где

.

Сделаем замену 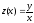,,, тогда

.

Разделим переменные и интегрируя, будем иметь

, ,

или .

Подставляя , получим общее решение исходного д.у.:

, .

Ответ:.

1.4. Линейные дифференциальные уравнения.

Д.у. первого порядка называется линейным, если оно имеет вид

(1.6)

Если , то уравнение называется линейным однородным.

Решить линейное уравнение (1.6) можно методом Бернулли. Согласно этому методу решение уравнения (1.6) ищется в виде , где– некоторые неизвестные функции. Тогда. Подставляя эти выражения в уравнение (1.6) и группируя слагаемые, содержащие(или), получим

,

. (1.7)

Пользуясь тем, что одна из неизвестных функций (например, ) может быть выбрана произвольно (), поскольку лишь произведениедолжно удовлетворять уравнению (1.6), функциявыбирается так, чтобы она обращала в нуль коэффициент прив левой части уравнения (1.7), т.е.

(1.8)

Это уравнение с разделяющимися переменными относительно функции . Проинтегрировав его

,

получим .

За принимаем любое отличное от нуля частное решение уравнения (1.8):.

Поставляя найденную функцию в левую часть (1.7), получим уравнение с разделяющимися переменными относительно:

.

Решив его, найдем

Перемножая функции и, будем иметь

.

Пример 3. Найти общее решение дифференциального уравнения .

Решение: Согласно методу Бернулли ,Подставим эти выражения в исходное уравнение

.

Сгруппируем члены, содержащие :

. (1.9)

Функцию найдем из уравнения

или ,

Разделяя переменные и интегрируя, имеем

, или.

Подставим найденное в уравнение (1.9):

или .

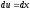Откуда

Перемножая и, получим общее решение

.

Ответ:

2. Дифференциальные уравнения высших порядков.

2.1. Общие понятия и определения.

Уравнение вида

,

где - независимая переменная,- искомая функция, а функцияопределена и непрерывна в некоторой областии зависит от, называется обыкновенным дифференциальным уравнением- го порядка.

Д.у. -го порядка, разрешенное относительно старшей производной имеет вид

,

где функция непрерывна в некоторой областиизменения своих аргументов.

Ограничимся рассмотрением д.у. второго порядка, т.е. уравнениями вида

(2.1)

и

(2.2)

Решением уравнения на интервале называется функция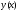, удовлетворяющая условиям:

1) дважды непрерывно дифференцируема на;

2) при любом;

3) обращает (2.2) в тождество:

при любом .

Задачей Коши для уравнения (2.2) называется задача нахождения решения уравнения , удовлетворяющего начальным условиям

(2.3)

где точка принадлежит областив которой задана.

Теорема Коши. Пусть в каждой точке области функцияи ее частные производные поинепрерывны, тогда для любой точкизадача Коши для уравнения (2.2) имеет единственное решение

Функция (2.4),

где - произвольные постоянные, называется общим решением уравнения (2.2) в области, если

а) функция 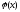имеет непрерывные частные производные подо второго порядка включительно;

б) для любой точки системаединственным образом разрешима относительно постоянных;

в) функция является решением д.у. (2.2) при любых допустимых значениях произвольных постоянных.

Если общее решение (2.4) в области задано неявно соотношением

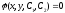(2.5),

то (2.5) называется общим интегралом уравнения (2.2) в области