
- •Министерство образования и науки
- •1. Вычислить неопределенный интеграл.
- •2. Вычислить неопределенный интеграл.
- •3. Вычислить неопределенный интеграл.
- •4. Вычислить неопределенный интеграл.
- •5. Проинтегрировать дробно-рациональную функцию.
- •6. Вычислить неопределенный интеграл.
- •7. Вычислить неопределенный интеграл.
- •8. Вычислить определенный интеграл.
- •9. Вычислить определенный интеграл.
- •10. Вычислить площадь фигуры, ограниченной линиями, заданными в декартовых координатах. Сделать чертеж.
- •11. Вычислить площадь фигуры, ограниченной линиями, заданными параметрическими уравнениями. Сделать чертеж.
- •12. Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах. Сделать чертеж.
- •13. Вычислить длины дуг кривых, заданных параметрическими уравнениями.
- •14. Вычислить объемы тел, образованных вращением фигур, ограниченных графиками функций.
- •15. Выяснить сходимость несобственного интеграла.
- •Методические указания к выполнению индивидуальных домашних заданий
- •Неопределенный интеграл
- •Основные методы интегрирования.
- •1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию.
- •2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию.
- •3) Интегралы вида: ,.
- •1) Интегралы вида , где m и n- целые числа.
- •2) Интегралы вида , гдеивходят в подынтегральную рациональную функцию, только в четных степенях.
- •3) Интегралы вида , гдеивходят в подынтегральную рациональную функцию в нечетных степенях.
- •2) Если в подынтегральную функцию входят радикалы с разными показателями вида , и т.Д. Или,и т.Д.
- •3) Интеграла вида .
- •4) Тригонометрические подстановки.
- •Определенный интеграл и его приложения
- •Несобственный интеграл
Министерство образования и науки
Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
Неопределенный, определенный и несобственные интегралы.
Индивидуальные домашние задания и методические указания для их выполнения
по курсу «Математика»
для студентов 1-го курса направления «Машиностроение»
Волгодонск 2014
УДК 811.111-36 (076.5)
Рецензент д.т.н., проф. Сысоев Ю.С.
Алексеева М.А., Батаков А.И., Кремлев А.Г., Лисичкина О.М., Столяр Л.Н., Чабанова Н.И. Неопределенный, определенный и несобственные интегралы. Индивидуальные задания и методические указания для их выполнения: учеб.-метод. пособие/Алексеева М.А., Батаков А.И., Кремлев А.Г., Лисичкина О.М., Столяр Л.Н., Чабанова Н.И.– Волгодонский инженерно-технический институт (ф) НИЯУ МИФИ. – Волгодонск, 2014, - 80 с.
Предназначено для студентов 1-го курса направления «Машиностроение»
© ВИТИ НИЯУ МИФИ, 2014
© Коллектив авторов, 2014
1. Вычислить неопределенный интеграл.
1.
а)
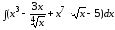 ;
б)
;
б)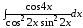 .
.
2.
а)
 ;
б)
;
б)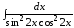 .
.
3.
а)
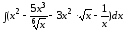 ;
б)
;
б)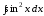 .
.
4.
а)
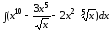 ;
б)
;
б) .
.
5.
а)
 ;
б)
;
б)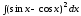 .
.
6.
а)
 ;
б)
;
б) .
.
7.
а)
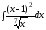 ;
б)
;
б) .
.
8.
а)
 ;
б)
;
б)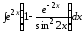 .
.
9.
а)
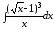 ;
б)
;
б)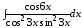 .
.
10.
а)
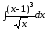 ;
б)
;
б) .
.
11.
а)
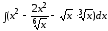 ;
б)
;
б)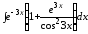 .
.
12.
а)
 ;
б)
;
б)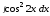 .
.
13.
а)
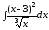 ;
б)
;
б)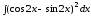 .
.
14.
а)
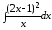 ;
б)
;
б)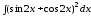 .
.
15.
а)
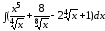 ;
б)
;
б) .
.
16.
а)
 ;
б)
;
б)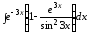 .
.
17.
а)
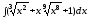 ;
б)
;
б)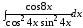 .
.
18.
а)
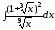 ;
б)
;
б) .
.
19.
а)
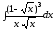 ;
б)
;
б)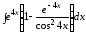 .
.
20.
а)
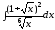 ;
б)
;
б)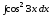 .
.
21.
а)
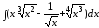 ;
б)
;
б)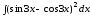 .
.
22.
а)
 ;
б)
;
б)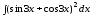 .
.
23.
а)
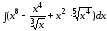 ;
б)
;
б)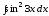 .
.
24.
а)
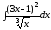 ;
б)
;
б)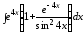 .
.
25.
а)
 ;
б)
;
б) .
.
26.
а)
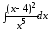 ;
б)
;
б) .
.
27.
а)
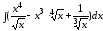 ;
б)
;
б)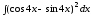 .
.
28.
а)
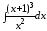 ;
б)
;
б) .
.
29.
а)
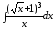 ;
б)
;
б)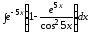 .
.
30.
а)
 ;
б)
;
б)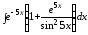 .
.
2. Вычислить неопределенный интеграл.
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12.
|
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
|
19.
|
20.
|
21.
|
|
22.
|
23.
|
24.
|
|
25.
|
26.
|
27.
|
|
28.
|
29.
|
30.
|
3. Вычислить неопределенный интеграл.
|
1. |
а)
|
б)
|
|
2. |
а)
|
б)
|
|
3. |
а)
|
б)
|
|
4. |
а)
|
б)
|
|
5. |
а)
|
б)
|
|
6. |
а)
|
б)
|
|
7. |
а) |
б) |
|
8. |
а)
|
б)
|
|
9. |
а)
|
б)
|
|
10. |
а)
|
б)
|
|
11. |
а)
|
б)
|
|
12. |
а)
|
б)
|
|
13. |
а)
|
б)
|
|
14. |
а)
|
б)
|
|
15. |
а)
|
б)
|
|
16. |
а)
|
б)
|
|
17. |
а)
|
б)
|
|
18. |
а)
|
б)
|
|
19. |
а)
|
б)
|
|
20. |
а)
|
б)
|
|
21. |
а)
|
б)
|
|
22. |
а)
|
б)
|
|
23. |
а)
|
б)
|
|
24. |
а)
|
б)
|
|
25. |
а)
|
б)
|
|
26. |
а)
|
б)
|
|
27. |
а)
|
б)
|
|
28. |
а)
|
б)
|
|
29. |
а)
|
б)
|
|
30. |
а)
|
б)
|

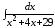 ;
;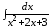 ;
;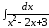 ;
; ;
; ;
;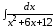 ;
;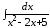 ;
;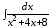 ;
;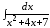 ;
; ;
; ;
;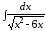 ;
;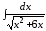 ;
;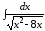 ;
;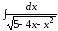 ;
; ;
;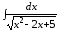 ;
;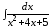 ;
; ;
; ;
; ;
; ;
;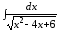 ;
;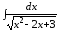 ;
;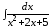 ;
; ;
;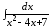 ;
;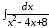 ;
;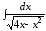 ;
; .
.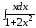 ;
; ;
;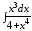 ;
;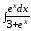 ;
;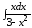 ;
;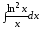 ;
; ;
;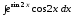 ;
; ;
;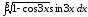 ;
;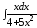 ;
; ;
; ;
;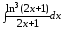 ;
;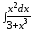 ;
; ;
;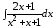 ;
;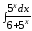 ;
;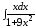 ;
; ;
;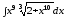 ;
;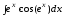 ;
; ;
; ;
;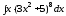 ;
; ;
;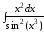 ;
;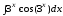 ;
; ;
; ;
;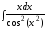 ;
;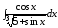 ;
; ;
; ;
;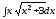 ;
;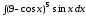 ;
;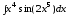 ;
;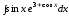 ;
;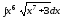 ;
;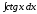 ;
;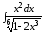 ;
; ;
;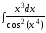 ;
; ;
;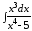 ;
; ;
;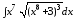 ;
;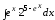 ;
; ;
;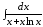 ;
; ;
;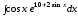 ;
; ;
;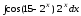 ;
; ;
;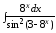 ;
; ;
; ;
;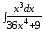 ;
; .
.