Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами

Это уравнения вида: , гдеp и g – числа(*)

Определение: Уравнение - называетсяхарактеристическим уравнением дифференциального уравнения (*) – обычное квадратное уравнение, решение которого зависит от D, возможны следующие случаи:

1)D>0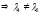- два действительных различных решения.

2)D=0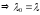- один действительный корень кратности 2.

3)D<0- два комплексно сопряжённых корня.

Для каждого из этих случаев укажем фундаментальную систему решений, составленную из 2 функций и.

Будем показывать что:

1) и- ЛНЗ

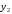2) и- решение (*)

Рассмотрим 1 случай D>0- 2 действительных различных корня.

Характеристическое уравнение:

В качестве ФСР возьмём:

а) покажем ЛНЗ

б) покажем, что - решение (*), подставим

+ p+g=0

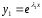верное равенство решение (*)

аналогично показывается для y₂.

Вывод: - ФСР (*) общее решение

Рассмотрим 2случай: D=0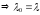- 1 действительный корень кратности 2.

В качестве ФСР возьмём:

ЛНЗ: 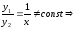ЛНЗ есть.

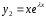- решение уравнения (см. 1 случай). Покажем что - решение.

подставим в ДУ

- решение.

Вывод: ФСР

Пример:

3 случай: D<0- 2 комплексно сопряжённых корня.

подставим в характ. уравнение

комплексное число равно 0, когда действительная и мнимая часть равны 0.

- будем использовать.

Покажем, что 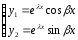- образуют ФСР.

А)ЛНЗ:

Б) 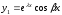- решение ДУ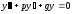

верное равенство- решение ДУ.

Аналогично показывается, что тоже решение.

Вывод: ФСР:

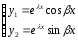
Общее решение:

Пример:

Если заданы н.у.

- то сначала находят общее решение , его производную:, а потом в эту систему подставляют н.у и находяти.

Пример:

Н.у:

Линейные однородные ду порядка n с постоянными коэффициентами

Это уравнения вида: , где а_i – числа.

Характеристическое уравнение будет иметь вид:

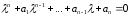
Слева стоит многочлен степени n, который имеет n корней с учётом их кратности и комплексности, следовательно, ФСР будет состоять из n решений:

1. Каждому простому корню характеристического уравнения , (имеющему кратность 1) ставится в соответствие

2. Каждому действительному корню кратностиr ставится в соответствие r решений:

3. Каждой паре комплексно сопряжённых корней 2 фундаментальных решения:

4. Если пара комплексно сопряжённых корней имеет кратность 2 и выше, то ФСР строятся аналогично 2 случаю.

Общее решение уравнения – линейная комбинация фундаментальных решений

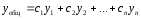
Основная трудность состоит в том, чтобы правильно решить характеристическое уравнение.

Пример:

Линейные неоднородные ду

Это уравнения вида:

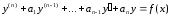
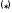
Теорема об общем решении ДУ: Общее решение ДУ(*) имеет вид:

, где - общее решение соответствующего однородного уравнения.

Доказательство: подставим в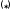

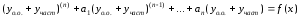
раскроем скобки и перегруппируемся:

(верно)

Если даны н.у

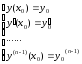
нужно показать, что все константы находятся однозначно

, где ФСР

Продифференцируем нужное количество раз и подставим н.у

получим систему n-линейных уравнений с n неизвестными . Определитель этой системы

- определитель Вронского системы функций .

Т.к - ФСРлинейная система имеет единственное решение и все константы находятся однозначно.

Конец доказательства.

Замечание: Общее решение соответствующего однородного уравнения

- линейная комбинация ФСР – известно

Основная трудность нахождения y_ч – решения неоднородного уравнения.