Однородные дифференциальные уравнения 1 порядка
Определение:
Функция
называется однородной порядкаn,
если
Пример:
- однородная функция порядкаn=2
Т.к
Определение: Однородная функция порядка 0 называется однородной.
Определение:
Дифференциальное
уравнение
называется однородным, если
-
однородная функция, т.е
Заменим
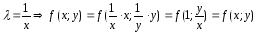
Таким образом однородное дифференциальное уравнение может быть записано в виде:
С
помощью замены
,
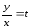гдеt
– функция переменной х, однородное
дифференциальное уравнение сводится
к уравнению с разделяющимися переменными.
Замена
-
подставим в уравнение
Переменные разделены, проинтегрируем обе части уравнения
Сделаем
обратную замену, подставив вместо
, получим общее решение в неявном виде.
Пример:
Однородное дифференциальное уравнение может быть записано в дифференциальной форме.
M(x;y)dx+N(x;y)dy=0, где M(x;y) и N(x;y) – однородные функции одинакового порядка.
Разделим
на dx
и выразим
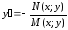
Пример:
1)
Линейные дифференциальные уравнения 1 порядка
Линейные
дифференциальные уравнения это вида
,
гдеP(x),
Q(x)
– непрерывные функции.
и
входят в уравнение линейно, т.е не
перемножаются между собой.
Сделаем
замену:
Приравняем скобку к 0
подставим
- дифференциальное
уравнение с разделяющимися переменными.
константу
интегрирования не прибавляем, т.к
достаточно одного частного решения.
Выразим
явно
Подставим
в
(*)
Выразим
Т.к
,
то проинтегрируем обе части последнего
уравнения по х
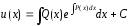
Общее решение линейного уравнения:
- всегда получается
в явном виде.
Пример:
1)
2)
y(1)=2
Уравнения Бернулли
,
где
;1
Решаются такие уравнения так же как и линейные
Замена
Явно
-
дифференциальное уравнение с разделяющимися
переменными.
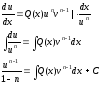
выразим
явно u
и найдём общее решение
Примеры:
1)
Дифференциальные уравнения высших порядков
Определение: Дифференциальное уравнение порядка n называется уравнение вида:
уравнение
вида:
– называетсяуравнением
разрешенным относительно старшей
производной.
Для такого уравнения справедлива теорема
Коши.
Теорема Коши.
Если
функция
в
(*) непрерывна вместе с частными
производными:
в области содержащей
значения
,
то существует единственное решение
дифференциального уравнения
удовлетворяющее начальным условиям:
Замечание:
для дифференциальных уравнений 2 порядка
начальные условия имеют вид:
Решить дифференциальное уравнение порядка n означает:
1)Найти общее решение (общий интеграл)
2)Найти частное решение (частный интеграл), удовлетворяющее заданным условиям.
Определение: Общим решением дифференциального уравнения 2 порядка
является функция
,
такая что:
1) при любых значениях с1 и с2 эта функция – решение.
2) каковы бы ни были начальные условия на области, в которой выполняется теорема Коши всегда можно подобрать значения с1 и с2 удовлетворяющие начальным условиям.
Определение: Частным решением дифференциального уравнения 2 порядка является решение, при конкретных значениях с1 и с2.
Замечание:
общее решение дифференциального
уравнения 2 порядка может быть получено
в неявном виде:
Дифференциальные уравнения 2 порядка, допускающие понижение порядка
1)
Уравнения вида:
уравнение решается двукратным интегрированием по переменной х.
Проинтегрируем 1 раз по х.
Проинтегрируем 2 раз по х
общее решение.
Замечание:
для дифференциального уравнения порядка
n:
-
интегрировать нужноn
раз.
Примеры:
2) Дифференциальные уравнения не содержащие явно y.
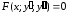- нет явно y
Замена
Подставим
замену в дифференциальное уравнение,
получим
получим дифференциальное уравнение 1 порядка.
Найдём решение этого уравнения:
сделаем
обратную замену
проинтегрируем
обе части по х
-
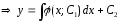общее решение
Пример:
3) Дифференциальные уравнения 2 порядка не содержащие явно х.
-
нет явно х.
Замена:
у-новая переменная
-
новая функция
-
её производная
Подставим замену в исходное уравнение
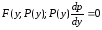
получим дифференциальное уравнение 1 порядка:
-
его решение
Сделаем
обратную замену -
-
дифференциальное уравнение с разделяющимися
переменными. Разделим переменные:
;
-
общее решение (вид неявный)
Примеры:
1.
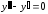
2.
