- •1. Методы проецирования. Комплексный чертеж
- •1.1. Введение. Цель и задачи курса
- •1.2. Понятие о методах проецирования
- •1.3. Свойства ортогонального проецирования
- •1.4. Методы прямоугольного проецирования на две и три взаимно перпендикулярные плоскости проекций. Проекции точки, комплексный чертеж.
- •1.4.1. Метод Монжа, комплексный чертеж.
- •1.4.2. Ортогональные проекции точки в системе двух плоскостей проекций
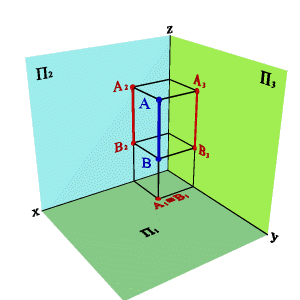
- •1.4.2. Ортогональные проекции точки в системе трех плоскостей проекций
- •2. Проекции прямой
- •2.1. Прямые общего и частного положения
- •2.2. Следы прямой линии
- •2.3. Определение натуральной длины отрезка прямой и углов ее наклона к плоскостям проекций
- •2.4. Отображение взаимного положения двух прямых
- •1. Параллельные прямые линии.
- •2. Пересекающиеся прямые.
- •3. Скрещивающиеся прямые
- •3. Проекции плоскости
- •3.1. Способы задания плоскости на чертеже
- •3.2. Точка и прямая в плоскости
- •3.3. Линии особого положения плоскости
- •3.3. Положение плоскостей относительно плоскостей проекций
- •3.4. Отображение относительного положения двух плоскостей
- •3.4.1. Параллельные плоскости
- •3.4.2. Пересекающиеся плоскости
- •3.4.3. Взаимно перпендикулярные плоскости
- •3.5. Отображение относительного положения прямой и плоскости
- •3.5.1. Параллельность прямой и плоскости
- •3.5.2. Пересечение прямой с плоскостью
- •3.5.3. Перпендикулярность прямой и плоскости
- •Преобразование чертежа
- •4.1. Способ замены плоскостей проекций
- •4.2. Способ вращение вокруг проецирующих прямых
- •4.3. Способ плоско-параллельного перемещения
- •5. Поверхности
- •5.1. Многогранники. Построение точки на поверхности многогранника
- •5.2. Кривые поверхности. Классификация поверхностей. Проецирование поверхностей
- •5.3. Пересечение поверхностей плоскостями
- •5.4. Взаимное пересечение поверхностей
- •6. Развертки поверхностей
- •7. Аксонометрические проекции
- •7.1. Образование аксонометрических проекций
- •7.2. Стандартные аксонометрические проекции
- •7.3. Аксонометрические проекции окружностей, параллельных плоскостям проекций
- •7.4. Аксонометрические построения
2. Проекции прямой
2.1. Прямые общего и частного положения
Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис. 12).
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 12. Прямая общего положения | |||
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.13). Для любой пары точек горизонтали должно быть справедливо равенство
zA=zB Þ A2B2 // 0x; A3B3 // 0y
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 13. Горизонтальная прямая | |||
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными (рис.14).
yA=yBÞ A1B1 // 0x, A3B3 // 0z
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 14. Фронтальная прямая | |||
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис.15).
xA=xB Þ A1B1 // 0y, A2B2 // 0z
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 15. Профильная прямая | |||
3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Фронтально проецирующая прямая - АВ (рис. 16).
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 16. Фронтально проецирующая прямая | |||
3.2. Профильно проецирующая прямая - АВ (рис. 17)
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 17. Профильно-проецирующая прямая | |||
3.3. Горизонтально проецирующая прямая - АВ (рис.18)
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 18. Горизонтально-проецирующая прямая | |||
2.2. Следы прямой линии
Следом прямой линии называется точка (рис. 19), в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю).
Горизонтальный след - М (zM)=0 – точка пересечения прямой с горизонтальной плоскостью проекций.
Фронтальный след - N (yN)=0 – точка пересечения прямой с фронтальной плоскостью проекций.
Профильный след - Т (xТ) = 0 – точка пересечения прямой с профильной плоскостью проекций.
|
|
|
|
|
|
| |||
|
| |||
|
а) модель |
б) эпюр | ||
|
Рисунок 19.Следы прямой линии в системе трех плоскостей проекций | |||
Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N2ºN, а N1 лежит на оси x, N3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила:
|
|
|
1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью x0 и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой. 2. Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой. С помощью этих правил найдены на эпюре следы прямой а (рис.20). Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта. |
|
Рисунок 20. Нахождение горизонтального и фронтального следов прямой линии | ||