6. Развертки поверхностей

Развертка пирамиды. Развертка пи­рамиды осуществляется в следующем по­рядке:

а) определяют истинную величину всех ребер пирамиды любым из известных спо­собов. На рис. 85 способом вращения найдена длина боковых ребер и способом замены плоскостей проекций определено основание пирамиды;

б) по найденным трем сторонам (рис. 86) строят какую-либо из боковых граней, например SoAoBo, пристраивая к ней следующую SoBoCo, а затем и осталь­ные грани (масштаб развертки уменьшен);

в) достраивают основание пирамиды A₀B_oC_oD_o.

Точки, расположенные внутри контура развертки, находятся во взаимно одноз­начном соответствии с точками поверхно­сти многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки. При­мером первой пары точек на рисунках слу­жат точки Ко, а иллюстрацией второго случая являются точки М и Мо.

Для определения точки Ко на развертке пришлось по ее ортогональным проекциям (рис. 85) найти длины отрезков AM (спо­собом замены плоскостей проекций) и SK (способом вращения). Эти отрезки и были использованы затем при построении на развертке сначала прямой SoMo и, нако­нец, точки Ко.

Развертка призмы. В общем случае развертка призмы выполняется следую­щим образом. Преобразуют эпюр так, что­бы боковые ребра призмы стали парал­лельны новой плоскости проекций (рис. 87). Тогда на эту плоскость боковые ребра спроецируются в истинную величину.

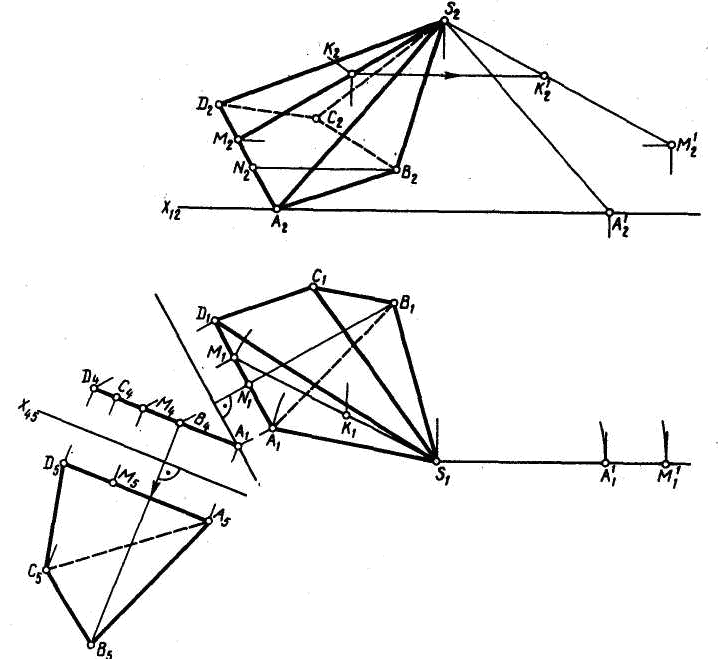
Рисунок 85

Пересекая призму вспомогательной плоскостью α, перпендикулярной ее боко­вым ребрам, строят проекции фигуры нор­мального сечения — треугольника /, 2, 3, а затем определяют истинную величину этого сечения. На рис. 87 она найдена способом вращения.

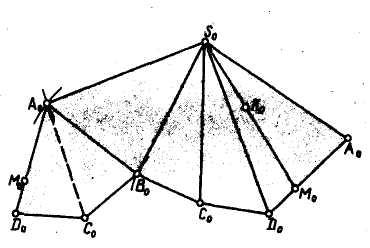
Рисунок 86

Рисунок 87

Рисунок 88

В дальнейшем строят отрезок 1о—1'о (рис. 88), равный периметру нормаль­ного сечения. Через точки 1о, 2о, 3о и 4о проводят прямые, перпендикулярные 1о—1'о, на которых откладывают соответствую­щие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 1о, отложены отрезки 1оDo=1₄D₄ и 1оА₀ = 1₄А₄.

Рисунок 89

Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Если требуется, достраивают ос­нования призмы.

В частном случае, когда основание при­змы на одну из плоскостей проекций прое­цируется в истинную величину (рис. 89), развертка ее боковой поверхности осуще­ствляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций. Затем в новой системе П₄/П₁ проводят некоторую плоскость α║П₄ (например, через ребро призмы AD) и совмещают с этой плоскостью боковую грань ADFB, вращая ее вокруг фронтали AD.

При вращении грани (параллелограм­ма) вокруг стороны AD фронтальные про­екции точек F и В перемещаются на эпюре по перпендикулярам к A₄D₄ .

Так как после совмещения с плоскостью α все стороны грани ADFB спроецируются на П₄ без искажения, то вершины F и В окажутся удаленными от неподвижных точек оси вращения А и D на расстояние, равное истинной длине АВ или DF. Но отрезки АВ и DF проецируются на П₁ в натуральную величину. Таким образом, засекая перпендикуляры, по которым пе­ремещаются точки F₄ и B4 дугой радиуса l_АВ, можно получить искомые точки раз­вертки Fo и Вo.

Следующую грань BFGC вращают во­круг ребра BF. На перпендикулярах, по которым перемещаются точки G₄ и С₄, делаются засечки из точек Fo и Во дугой радиуса l_ВС. Аналогично строится раз­вертка последней боковой грани призмы.

Построение на развертке точки К, при­надлежащей грани ADGC, ясно из рис. 89. Предварительно через эту точку по грани параллельно боковым ребрам проведена прямая NM, которая затем по­строена на развертке.

Развертки цилиндрической и конической поверхностей. Развертка цилиндрической поверхности выполняется аналогично развертке при­змы. Предварительно в заданный цилиндр вписывают n-угольную призму.

На рис. 90 выполнена развертка на­клонного эллиптического цилиндра. Так как нижнее основание его параллельно горизонтальной плоскости проекций, то для построения развертки использован способ раскатки. Параллельность образующих цилиндра горизонтальной плоскости проекций делает возможным выпол­нить развертку без предварительного пре­образования проекций.

Рисунок 90

Развертка конической поверхности вы­полняется аналогично развертке пирами­ды в следующем порядке. Сначала в за­данный конус вписывают n-угольную пи­рамиду (число п, зависящее от размеров и масштаба чертежа, следует брать в пре­делах от 8 до 12). Затем строят развертку боковой поверхности вписанной пирамиды. Соединив концы ребер плавной кривой, получают прибли­женную, развертку боковой поверхности конуса.

На рис. 91 выполнено построение раз­вертки наклонного эллиптического конуса, заданного круговым основанием, лежа­щим в горизонтальной плоскости, и вер­шиной S. Истинная величина боковых ре­бер вписанной восьмиугольной пирамиды найдена способом вращения. Точка М, лежащая на поверхности конуса, перене­сена на развертку так же, как и при раз­вертке пирамиды.

Рисунок 91