Математическое планирование эксперимента для проведения регрессионного анализа

В современных условиях, учитывая многогранность изучаемых явлений, острый дефицит времени, высокую стоимость эксплуатации научного оборудования, необходимо стремиться к наиболее рациональным планам проведения эксперимента.

Во многих случаях полученное по результатам эксперимента уравнение регрессии используется как математическая модель объекта.

Математические модели объекта могут быть детерминированными и статистическими.

Детерминированные математические моделиобъекта, строят на основе фундаментальных законов физики, механики, химии и других естественных наук.Статистические математические модели получают, описывая зависимости выходных параметровy_v(свойств, откликов) объекта от изменения входных параметровx_j(факторов) с помощью различных функций

y_v = _v (x₁, x₂, x₃, ..., x_j, ..., x_k) +  (w₁, w₂, w₃, ..., w_z, ...) ,

где  – вклад в изменение свойств объекта случайных факторов.

Наиболее часто в качестве статистической модели объекта используют приближенные уравнения регрессии ŷ:

ŷ = f_v(x₁, x₂, x₃, …, x_j, …, x_k);

y_v = f_v(x₁, x₂, x₃, ..., x_j, ..., x_k) +  + .

Одно из основных требований к математической модели объекта - это точность описания (предсказывания) поведения реального объекта при изменении условий.

Применение методов РАМПЭможет помочь получить уравнения регрессии, более точно описывающего реальный объект(с меньшими ошибками + ), чем уравнение, полученное при КРА. В некоторых случаях применение методов математического планирования эксперимента позволяет значительно сократить в нем число опытов.

В основу методов математического планирования эксперимента для проведения РА положен принцип "черного ящика". Суть этого принципа заключается в том, что исследователь, не зная об истинных закономерностях поведения объекта, описывает его с помощью статистических математических моделей.

Образно говоря, "ударяя" по исследуемому объекту изменением входных параметров (x_j) в ходе эксперимента (рис. 6) и измеряя его реакцию (y_v) на эти "удары" при действии случайных факторов (w_z), можно получить статистическую математическую зависимость, пригодную для прогноза поведения объекта.

Рис. 6. Схема объекта,

изучаемого методом

"черного ящика"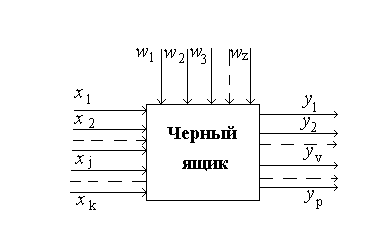

С помощью метода "черного ящика" получают статистические математические модели объектов в виде полиномов различной степени.

Известно, что любую функцию (в том числе ) можно разложить в ряд Тейлора и представить в виде конкретного полинома определенной степени (конечного отрезка ряда Тейлора) вида

…,

ŷ =

где  и b – генеральные и выборочные коэффициенты ряда Тейлора, соответственно.

По результатам эксперимента можно определить вид полинома только с выборочными коэффициентами, которые характеризуют:

b₀ – величину y при нулевом значении всех факторов (свободный член);

b₁, b₂, ..., b_j, ..., b_k – линейные эффекты влияния соответствующих факторов на величину y;

b₁₂, b₁₃, ..., b_1j, ...,b_1k, b₂₃, b₃₄, ..., b_2j, ..., b_(k-1)j, ..b_(k-1)k – парные эффекты влияния соответствующих факторов на величину y (эффекты взаимодействия двух соответствующих факторов);

b₁₁, b₂₂, ..., b_jj, ..., b_kk – квадратичные эффекты влияния соответствующих факторов на величину y;

b₁₂₃, b₁₂₄, ..., b_1uj, ..., b₂₃₄, b₂₃₅, ..., b_2uj, ..., b_(k-2)(k-1)k – тройные эффекты влияния соответствующих факторов на величину y (эффекты взаимодействия трех соответствующих факторов) и т.д.

Наиболее удобно планировать эксперимент математическими методами для кодированных значений факторов (x_j), получаемых из натуральных значений (X_j) по следующим формулам:

; ;,

где – натуральное значение фактора в центре (середине) выбранной (заданной) области изменения (варьирования) фактора,и– максимальное и минимальное значения фактора в выбранной области его изменения, соответственно;Х_j – шаг варьирования фактора. В соответствии с этими формулами натуральному значению X_j = соответствует кодированное значениеx_j = 0; X_j = – кодированное значениеx_j = +1, а X_j = – значениеx_j = –1.

Переход от кодированных значений факторов к натуральным осуществляют по формуле

.

Выбор плана эксперимента для проведения РАМПЭ, в отличие от планирования экспериментов для проведения КРА, определяется видом выбранного семейства функций (видом полинома).

После завершения эксперимента для проведения РАМПЭ выполняют следующие действия:

1. Выбирают вид полинома (отрезок ряда Тейлора) для поиска уравнения регрессии.

2. Для выбранного полинома с помощью МНК рассчитывают параметры функции (выборочные коэффициенты уравнения регрессии).

3. Проверяют рассчитанные выборочные коэффициенты уравнения регрессии на значимость (равенство нулю).

4. Корректируют вид исходной функции, исключая из нее члены с незначимыми коэффициентами.

5. Оценивают ошибки, допускаемые при описании истинной зависимости  с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью распределения Фишера или рассчитывают вероятность описания зависимости  функцией f.

6. Если точность найденного уравнения регрессии не удовлетворяет, то выбирают, планируют и реализуют другой план эксперимента для поиска уравнения регрессии в другом семействе полиномов (например, полиномов более высокого порядка).

Порядок проведения РАМПЭ в отличие от КРА имеет следующие особенности:

- выбирается только один класс функций – полиномы;

- используется только один метод приближения – МНК;

- после корректировки уравнения регрессии его коэффициенты не пересчитываются;

- выполняется меньшее количество этапов РА.

Обычно поиск уравнения регрессии начинают в семействе самых простых полиномов: первого и второго порядка. По названиям степеней полиномов называют и планы эксперимента для применения РАМПЭ.

Прежде чем перейти к знакомству с методами РАМПЭ, необходимо отметить некоторые важные обстоятельства [4].

1. С познавательной точки зрения полиноминальная статистическая модель объекта не представляет большого интереса. Зная оценки коэффициентов отрезков ряда Тейлора, нельзя определить истинную зависимость , а, следовательно, невозможно получить информацию о механизме поведения исследуемого объекта.

2. Полиноминальные модели справедливы только для условий, в которых проводился эксперимент.

3. Полиноминальные модели очень полезны с практической точки зрения, так как позволяют управлять поведением объекта и решать для него задачи оптимизации.