
MetodTM_vse_spets_Ctat_Kin
.pdf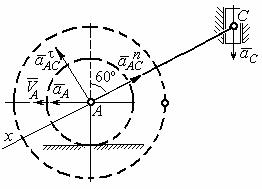
пендикулярно отрезку АС. На данном этапе величина вектора касательного ус-
корения не может быть вычислена, поскольку угловое ускорение шатуна АС
ε неизвестно. На рис. 2.17 направление вектора касательного ускорения rτ
AC aAC
выбрано из предположения, что вращение шатуна ускоренное и направление углового ускорения совпадает с направлением его угловой скорости.
Направление вектора aA ускорения точки А определяется из того, что центр барабана движется по прямой, параллельной горизонтальной поверхно-
сти качения. На рис. 2.17 направление вектора ускорения aA выбрано из пред-
положения, что качение барабана ускоренное.
Выберем ось х вдоль линии АС (рис. 2.18) и спроектируем векторное ра-
r |
|
r |
r |
r |
на эту ось. При таком выборе оси проекция неиз- |
||||||||
венство a |
A |
= a |
+ aτ |
+ an |
|||||||||
|
C |
AC |
AC |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
rτ |
обращается в нуль. |
|
|
|
|
|
|
|
вестного ускорения aAC |
|||||||
|
|
|
|
|
|
Получим |
a |
A |
cos30o = a |
cos60o − an . От- |
|||
|
|
|
|
|
|
|
|
|
|
C |
AC |
||
|
|
|
|
|
|
сюда |
найдём |
ускорение центра барабана |
|||||
|
|
|
|
|
|
aA = |
1 |
|
(aC cos60o − aACn ) = – 122,4 м/с2. |
||||
|
|
|
|
|
|
cos30o |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 2.18. Схема для определения |
Отрицательное значение ускорения точки А |
||||||||||||
означает, что на рис. 2.17 – 2.18 вектор ус- |
|||||||||||||
ускорения центра барабана |
|||||||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
корения |
aA должен иметь противополож- |
||||||
ное направление. Таким образом, вектор ускорения aA направлен в сторону,
противоположную вектору скорости VA , и движение барабана замедленное.
Для того, чтобы найти ускорение точки В, выразим его |
через полюс А на |
|||
r |
r |
r |
r |
– ускорение точки |
основании векторного равенства: aB = aA + aBAτ |
+ aBAn , где aA |
|||
rτ |
rn |
– касательная и нормальная состав- |
||
А, выбранной в качестве полюса; aBA , |
aBA |
|||
ляющие ускорения точки В при вращении барабана вокруг полюса А.
50

|
Модуль |
вектора нормального ускорения |
r |
||
|
aBAn равен по величине |
||||
an |
= w2 × BA = (10 |
|
|
||
3)2 × R = 150 м/с2. Вектор направлен вдоль радиуса бараба- |
|||||
BA |
1 |
|
|
|
|
на от точки В к полюсу А (рис. 2.17). |
|
||||
|
|
|
|
rτ |
вычисляется по формуле |
|
Модуль вектора касательного ускорения aBA |
||||
aτ |
= e × BA, |
где e – угловое ускорение барабана. Значение углового ускоре- |
|||
BA |
1 |
1 |
|
|
|
ния катящегося барабана (в отличии от углового ускорения eAC шатуна АС)
может быть найдено. Расчёт основан на том, что при движении барабана рас-
стояние АР1 от точки А до центра скоростей барабана Р1 остаётся постоянным,
равным r. Тогда выражение VA = w1 × AP1 = w1 × r для расчёта скорости точки А можно продифференцировать. Получим dVdtA = ddtω1 × r . Так как точка А движет-
ся по прямой, производная от скорости точки равна её полному ускорению, а
производная от угловой скорости барабана равна его угловому ускорению. То-
гда имеем aA = e1 × r , откуда находим угловое ускорение e1 = arA = 40,8 рад/с2, а
затем и модуль вектора касательного ускорения aBAτ = e1 × BA= 20,4 м/с2.
Заметим, что для вычисления углового ускорения eAC шатуна АС, подоб-
ные рассуждения неприменимы. Формулу VA = wAC × AP2 невозможно продиф-
ференцировать, так как при движении механизма расстояние АР2 от точки А до центра скоростей Р2 шатуна АС является неизвестной функцией времени.
Выберем систему координат хВу как показано на рис. 2.17 и спроецируем
r = r + rτ + rn
на эти оси векторное равенство aB aA aBA aBA . Полагая, что движение ба-
рабана ускоренное (т.е. вектора ускорений a и rτ направлены как показано на
A aBA
рис. 2.17), получим значения составляющих ускорения точки В: aBx = aA + aBAn , aBy = aBAτ . Подставляя значения ускорений, найдём aBy = 20,4 м/с2, aBx = -122,4 +150 = 27,6 м/с2. Вектор полного ускорения точки В направлен по
51
диагонали прямоугольника, построенного на векторах aBx , aBy . Величина уско-
рения точки В aB = 
 aBx2 + aBy2 = 34,32 м/с2.
aBx2 + aBy2 = 34,32 м/с2.
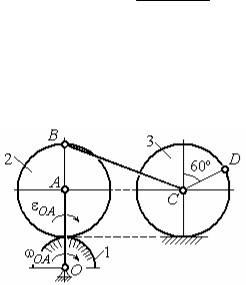
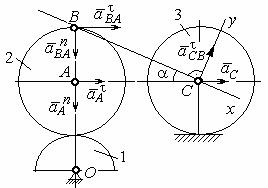
Задача 2. В плоском механизме (рис. 2.19) кривошип ОА вращается во-
круг оси О с угловой скоростью wOA и угловым ускорением eOA . Диск 2, шар-
нирно присоединённый к кривошипу в точке А, катится без проскальзывания по неподвижному диску 1. Радиусы дисков R1 и R2 . На краю диска 2 в точ-
ке В шарнирно прикреплен стержень
Рис. 2.19. Схема движения плоского ВС, соединенный с центром С диска 3.
механизма
Радиус диска 3 равен радиусу диска 2:
R3 = R2 . Диск 3 катится без скольжения вдоль горизонтальной прямой. Для положения механизма, изображенного на рис. 2.19, определить ускорение точки D и угловое ускорение стержня ВС, если: wOA = 4 рад/с, eOA = 2 рад/с2, R1 = 4 см, R2 = 8 см. Длина стержня ВС = 20 см.
Решение
Определение угловых скоростей звеньев механизма.
Рассмотрим вращательное движение кривошипа ОА. Скорость точки А:
VA = wOA × OA= 48 см/с. Вектор скорости VA направлен перпендикулярно кри-
вошипу ОА в сторону движения кривошипа (рис. 2.20).
При движении диска 2 точка P2 соприкосновения второго диска с непод-
вижным первым является мгновенным центром скоростей диска 2. Угловая
скорость диска 2: ω2 = |
VA |
= |
48 |
= 6 рад/с. Тогда скорость точки В диска 2: |
|
AP2 |
8 |
||||
|
|
|
VB = w2BP2 = 6·16 = 96 см/с.
Для определения угловой скорости стержня ВС заметим, что скорости двух точек стержня VB и VC параллельны, но точки В и С не лежат на общем
52
перпендикуляре к скоростям. В этом случае мгновенный центр скоростей стержня ВС отсутствует (бесконечно удалён), угловая скорость стержня равна
нулю: ωBC = 0, а стержень |
совершает |
|
|
|
|
|
|
|
|
|
||||||||
мгновенное поступательное движение. В |
|
|
|
|
|
|
|
|
|
|||||||||
результате, VC = VB = 96 см/с. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
При качении диска 3 по непод- |
|
|
|
|
|
|
|
|
|
|||||||
вижной поверхности без проскальзыва- |
|
|
|
|
|
|
|
|
|
|||||||||
ния точка P3 касания его с поверхностью |
|
|
|
|
|
|
|
|
|
|||||||||
является мгновенным центром |
скоро- |
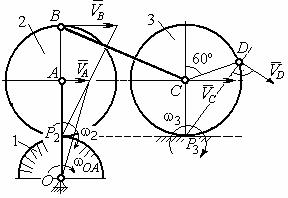
Рис. 2.20. Расчетная схема |
|
|||||||||||||||
стей. Тогда угловая |
скорость |
диска 3: |
|
|||||||||||||||
для определения угловых скоростей |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
w = |
VC |
= 12 |
рад/с. Скорость |
точки D |
|
|
звеньев механизма |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
|
CP3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
диска 3: VD = w3 × DP3 . Величину DP3 |
находим из треугольника P3DC . В ре- |
|||||||||||||||||
зультате, |
DP = 2R cos30o = 13,8 см и V |
D |
= 165,6 см/с. Вектор скорости V |
на- |
||||||||||||||
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
D |
||
правлен в сторону движения диска 3 перпендикулярно линии DP3 и (рис. 2.20). |
||||||||||||||||||
|
|
Определение ускорений точек механизма. |
|
|
|
|
|
|
|
|
||||||||
|
|
Представим |
ускорение |
aC |
|
точки |
|
С |
векторной |
суммой: |
||||||||
r |
|
r |
rn |
rτ |
где aB – ускорение точки В, выбранной в качестве полю- |
|||||||||||||
aC |
= aB + aCB + aCB , |
|||||||||||||||||
|
rn |
rτ |
нормальная |
и касательная составляющие ускорения точки С |
||||||||||||||
са; aCB , |
aCB – |
|||||||||||||||||
при вращении стержня ВС вокруг полюса В, an |
|
= w2 |
|
× CB , |
aτ |
= e |
CB |
× CB . |
||||||||||
|
|
|
|
|
|
|
|
|
CB |
CB |
|
CB |
|
|
||||
Нормальная составляющая ускорения точки С aCBn |
= 0, так как стержень СВ со- |
|||||||||||||||||
вершает мгновенное поступательное движение и |
wBC = |
0. Направление каса- |
||||||||||||||||
тельной составляющей rτ неизвестно, так как неизвестно направление углово-
aCB
го ускорения стержня eCB . Для определённости, выберем направление углового ускорения стержня ВС в сторону против хода часовой стрелки. На рис. 2.21 это направление показано дуговой стрелкой eCB . В соответствии с выбранным на-
53
|
rτ |
|
|
|
|
|
|
|
правлением углового ускорения вектор aCB строится перпендикулярно линии |
||||||||
|
стержня ВС в сторону углового ус- |
|||||||
|
корения eCB (см. рис. 2.21). |
|
|
|
||||
|
Выразим |
ускорение |
точки |
В |
||||
|
через полюс А: |
r |
r |
rn |
r |
τ |
, |
|
|
aB = aA + aBA + aBA |
|||||||
|
где aA – ускорение полюса А; |
r |
|
, |
||||
|
aBAn |
|||||||
|
rτ |
|
и касательная |
|||||
|
aBA – нормальная |
|||||||
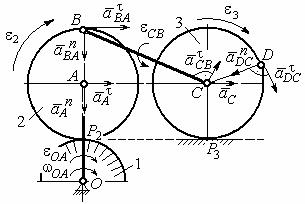
Рис. 2.21. Расчетная схема |
составляющие |
ускорения |
точки |
В |
||||
при вращении диска 2 вокруг полю- |
||||||||
для определения ускорений точек меха- |
||||||||
низма и угловых ускорений его звеньев |
са А. Величина нормальной состав- |
|||||||
|
||||||||
ляющей ускорения точки В aBAn = w22 × BA = 288 см/с2. Вектор |
r |
направлен |
||||||
aBAn |
||||||||
вдоль радиуса ВА от точки В к полюсу А (рис. 2.21). Касательное ускорение
точки В при вращении диска 2 |
вокруг полюса А вычисляется по формуле |
||||||||||||||||
aBAτ |
= e2 × BA . Для определения углового ускорения e2 диска 2 заметим, что во |
||||||||||||||||
время движения диска 2 расстояние АР2 остается постоянным, равным R2. Диф- |
|||||||||||||||||
ференцируя |
равенство V |
A |
= w |
2 |
× AP = w |
R , получим: |
dVA |
= |
dω2 |
R , или |
|||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 2 |
dt |
|
|
dt |
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
aτ = e |
R , откуда e |
2 |
= |
aAτ |
|
. При дифференцировании учтено, |
что точка А дви- |
||||||||||
|
|||||||||||||||||
A |
|
2 2 |
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
жется по окружности. В этом случае производная от скорости равна не полному ускорению точки, а только его касательной составляющей aτA . Для того, чтобы её найти рассмотрим вращательное движение кривошипа ОА вокруг непод-
вижной оси О. Ускорение точки А представляется в виде векторного равенства
r |
rn rτ |
rn |
и |
rτ |
|
|
aA = aA + aA , где |
aA |
aA – известные нормальная и касательная составляю- |
||||
щие |
ускорения |
|
точки А кривошипа ОА, an = w2 |
× OA = 192 см/с2, |
||
|
|
|
|
A |
OA |
|
τ |
|
|
2 |
. Вектор нормального ускорения |
rn |
направлен вдоль |
aA = eOA × OA = 24 см/с |
aA |
|||||
54
кривошипа от точки А к оси вращения – точке О (рис. 2.21), вектор касательно-
|
|
|
rτ |
|
|
|
|
го ускорения aA перпендикулярен кривошипу и направлен в сторону углового |
|||||||
ускорения |
εOA . |
|
|
|
|
||
|
С учётом вычисленного значения касательного ускорения точки А полу- |
||||||
|
|
|
|
|
|
aτ |
|
чим величину углового ускорения диска 2 ε2 = |
A |
= 3 рад/с2 и модуль каса- |
|||||
|
|||||||
|
|
|
|
|
|
R2 |
|
тельного ускорения aBAτ |
точки В при вращении диска 2 вокруг полюса А: |
||||||
aBAτ = e2 × BA = 24 см/с2. |
|
|
|
||||
|
После необходимых подстановок |
|
|
||||
для определения ускорения точки С |
|
|
|||||
имеем |
векторное |
равенство: |
|
|
|||
r |
rn |
rτ |
rn |
rτ |
rτ |
|
|
aC |
= aA + aA + aBA + aBA + aCB . Выбе- |
|
|
||||
рем |
оси |
Сx, |
Сy, |
как |
показано на |
|
|
рис. 2.22, – вдоль отрезка ВС и пер- Рис. 2.22. Расчетная схема для вычисления
пендикулярно ему и спроецируем на |
ускорения точки С |
|
|
||
|
|
|
|
||
них полученное векторное равенство. Получим |
|
|
|
|
|
aCcosα = aAnsina + aAτ cosa + aBAn sina + aBAτ cosa , |
|
|
|
||
aCsinα = aAn cosa+ aAτ sina + aBAn cosa + aBAτ sina + aCBτ , |
|
|
|
||
где α – угол между стержнем ВС и линией центров АС, sinα = |
AB |
= |
0,4; |
||
BC |
|||||
|
|
|
|
||
cosα = 0,92 . Решая систему найдём aC = 256,7 см/с2, aCBτ = – 358,12 см/с2. |
|
||||
|
rτ |
на |
|
рис. |
|
Знак «минус» означает, что вектор касательного ускорения aCB |
|
||||
2.21 – 2.22 следует направить в противоположную сторону. В соответствии с этим, выбранное на рис. 2.21 направление углового ускорения стержня ВС, по-
55
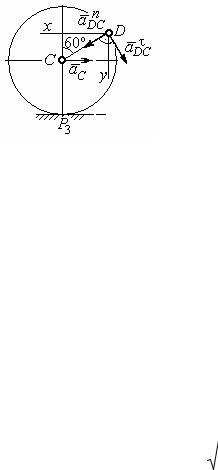
казанное дуговой стрелкой εCB , также следует заменить на противоположное.
Модуль углового ускорения стержня ВС: εCB = |
|
aCBτ |
|
= 17,9 рад/с2. |
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
BC |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим ускорение точки D через полюс С: |
r |
r |
rn |
rτ |
где |
||||||||||||||||||||||
|
aD = aC |
+ aDC |
+ aDC , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
rn |
|
rτ |
|
– нормальное и касательное со- |
||||||||||||||
aC – известное ускорение точки С; aDC |
, aDC |
|||||||||||||||||||||||||||
ставляющие ускорения точки D при вращении диска 3 вокруг полюса С. Вели- |
||||||||||||||||||||||||||||
чина нормального ускорения точки D an |
|
= w2 |
|
× DC = 1152 см/с2. Вектор уско- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
DC |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рения aDCn направлен по радиусу от точки D к полюсу С (рис.2.23). |
|
|
||||||||||||||||||||||||||
|
Для расчёта касательной составляющей aDCτ |
|
ускорения точки D найдём |
|||||||||||||||||||||||||
угловое |
ускорение |
диска 3. |
Продифференцируем |
|
по |
времени |
равенство |
|||||||||||||||||||||
V = w |
× CP |
= w R . Получим: |
dVC |
= |
dw3 |
R , |
|
или a |
C |
= e |
R . Здесь производ- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
C |
3 |
3 |
3 |
3 |
|
|
|
dt |
|
|
|
|
|
dt |
|
|
3 |
|
|
|
|
|
3 3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ная от скорости точки С равна ускорению этой |
|||||||||||||||||||||||
|
|
|
|
|
точки: |
|
dVC |
|
= aC , |
так как движение точки С явля- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ется прямолинейным. Угловое ускорение диска 3: |
|||||||||||||||||||||||
|
|
|
|
|
ε3 = |
aC |
|
= 32,09 |
рад/с2. Тогда величина касатель- |
|||||||||||||||||||
Рис.2.23. Расчетная схема |
R3 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
для определения ускоре- |
ной |
|
|
составляющей |
|
|
ускорения |
точки |
D |
|||||||||||||||||||
|
|
ния точки D |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
aDCτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= e3 × DC = |
256,7 |
см/с2. Направление вектора |
||||||||||||||||||||
rτ |
соответствует ускоренному движению диска 3. |
Проведём оси |
Dx и |
Dy |
||||||||||||||||||||||||
aDC |
||||||||||||||||||||||||||||
как показано на рис. 2.23 и спроецируем |
векторное равенство ускорения точки |
|||||||||||||||||||||||||||
D на оси: aDx = -aC + aDCn cos30o |
- aDCτ cos60o , |
aDy = aDCn cos60o + aDCτ cos30o . |
|
|||||||||||||||||||||||||
|
Решая |
систему находим |
значения |
|
|
проекций |
модуля |
ускорения |
||||||||||||||||||||
aDx = 612,5 см/с2, aDy = 798,3 см/с2. Величина ускорения точки D: |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
aD = |
aDx2 + aDy2 |
= 1006,2 см/с2. |
|
|
|
|
|
|||||||||||||||||
56

3.СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
3.1.Основные понятия сложного движения точки
Рассматривается подвижное твердое тело и точка, перемещающаяся отно-
сительно тела.
Траектория точки в её движении относительно тела называется относи-
тельной траекторией. Скорость точки в этом движении называют относитель-
ной скоростью, ускорение – относительным ускорением.
Траектория точки, перемещающейся вместе с телом, называется перенос-
ной траекторией точки, скорость точки при таком её движении – переносной скоростью, а ускорение – переносным ускорением.
Суммарное движение точки вместе с телом и относительно тела называ-
ется сложным движением. Траектория точки относительно неподвижной сис-
темы координат называется абсолютной траекторией точки, скорость и уско-
рение – абсолютной скоростью и абсолютным ускорением.
При вычислении абсолютной скорости используется теорема о сложении скоростей: при сложном движении абсолютная скорость точки равна гео-
метрической сумме относительной и переносной скоростей V = Ve + Vr , где
V , Ve , Vr – вектора абсолютной, переносной и относительной скоростей точки.
В случае, когда относительное движение точки задается естественным способом в виде закона изменения пути S = S(t) , величина относительной ско-
рости точки равна модулю производной: Vr = S&r . Если переносное движение точки есть вращение тела вокруг неподвижной оси, скорость точки в перенос-
ном движении будет: Ve = ωehe , где ωe – величина угловой скорости вращения тела, he – кратчайшее расстояние от места положения точки на теле до оси вращения тела.
57
При вычислении абсолютного ускорения используется теорема Кориоли-
са о сложении ускорений: при сложном движении абсолютное ускорение
точки равно геометрической сумме трех ускорений – относительного, пе-
реносного и ускорения Кориолиса a = ae + ar + aк , где a – вектор абсолютного ускорения точки; ae , ar –
вектора, соответственно, переносного
|
и |
относительного ускорений точки; |
||
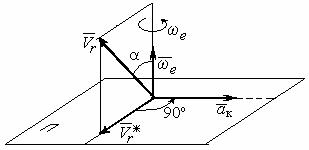
Рис. 3.1. Определение направления |
aк |
– вектор |
ускорения Кориолиса. |
|
ускорения Кориолиса по правилу |
(Иногда его называют поворотным |
|||
Жуковского |
||||
|
|
|
||
|
ускорением.) |
Вектор ускорения Ко- |
||
|
|
r |
r |
|
риолиса определяется векторным произведением aк = 2(ωe ×Vr ), где ωe – век-
тор угловой скорости переносного движения; Vr – вектор относительной скоро-
сти точки. Модуль ускорения Кориолиса равен: |
r |
= 2 |
r |
× |
|
Vr |
|
sina , где α |
– |
|
|
||||||||
aк |
we |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
угол между вектором угловой скорости переносного движения и вектором от-
носительной скорости точки. Направление вектора ускорения Кориолиса может быть получено по правилу построения вектора векторного произведения.
На рис. 3.1 показан способ выбора направления вектора ускорения Ко-
риолиса по правилу Н. Е. Жуковского. Правило состоит в следующем: пусть имеем точку, движущуюся с относительной скоростью Vr . Построим плоскость
П, перпендикулярную вектору угловой скорости ωe , и спроецируем вектор Vr
на эту плоскость. Проекцию обозначим Vr (см. рис. 3.1). Чтобы получить на-
правление ускорения Кориолиса, следует вектор проекции относительной ско-
рости Vr повернуть на 90° в плоскости П вокруг оси переносного вращения в направлении этого вращения. Если сложное движение точки происходит в плоскости, перпендикулярной оси переносного вращения, направление ускоре-
58
ния Кориолиса можно получить простым поворотом вектора относительной скорости на угол 90° вокруг оси переносного вращения в направлении этого вращения.
Относительное ускорение ar представляется как сумма векторов относи-
тельного |
касательного arτ |
и относительного |
нормального |
r |
|
|||||||||
arn ускорений: |
||||||||||||||
ar |
= arτ + arn . Переносное ускорение точки ae тела имеет своими составляющи- |
|||||||||||||
|
|
|
|
|
|
|
rτ |
|
|
rn |
ускорения так, что |
|||
ми переносное касательное ae |
и переносное нормальное ae |
|
||||||||||||
r |
|
r |
r |
|
|
|
|
|
|
|
|
|
|
|
a |
e |
= aτ + an . Таким образом, абсолютное ускорение точки в сложном движении |
||||||||||||
|
e |
e |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r |
r |
r |
|
r |
r |
r |
можно представить в виде векторного равенства a |
= arτ + arn |
+ aeτ + aen + aк . |
||||||||||||
|
|
Модули относительного касательного и относительного нормального ус- |
||||||||||||
корений |
при естественном способе задания относительного движения точки |
|||||||||||||
равны: aτ |
= V& , |
an = |
Vr2 |
, где ρ – радиус кривизны относительной траекто- |
||||||||||
|
||||||||||||||
|
|
|
r |
r |
r |
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рии. (При движении точки по окружности радиус кривизны равен радиусу ок-
ружности, при движении по прямой – бесконечности и в этом случае arn = 0 .)
Значения переносного касательного и нормального ускорений при вращатель-
ном |
переносном |
движении точки вычисляются по формулам: aτ = ε |
h , |
|||
|
|
|
|
|
e |
e e |
an = ω2h , |
где ε |
e |
– угловое ускорение вращательного переносного движения, |
|||
e |
e |
e |
|
|
|
|
εe = |
ωe |
, he – расстояние от точки до оси вращения тела; ωe – величина угло- |
||||
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
вой скорости вращения тела. Вектора ускорений строятся по общим правилам построения векторов нормального и касательного ускорений.
При поступательном переносном движении по прямой ωe = 0 ускорение Кориолиса и переносное нормальное ускорение равны нулю aк =0, aen = 0 . Пол-
ное переносное ускорение равно касательной составляющей, модуль которой вычисляется по формуле aeτ = V&e .
59
