Ковалевский. Книжки по геостатистике / EAGE_Kovalevsky_SLTRU_2011_Geological_Modelling_on_the_Base_of_Geostatistics

Подробно о реализациях мы будем говорить позже. Сейчас мы начнем новую главу, в которой рассмотрим кригинг точечных данных с использованием вспомогательной пространственной переменной.

57

4. Кригинг с использованием вспомогательной переменной

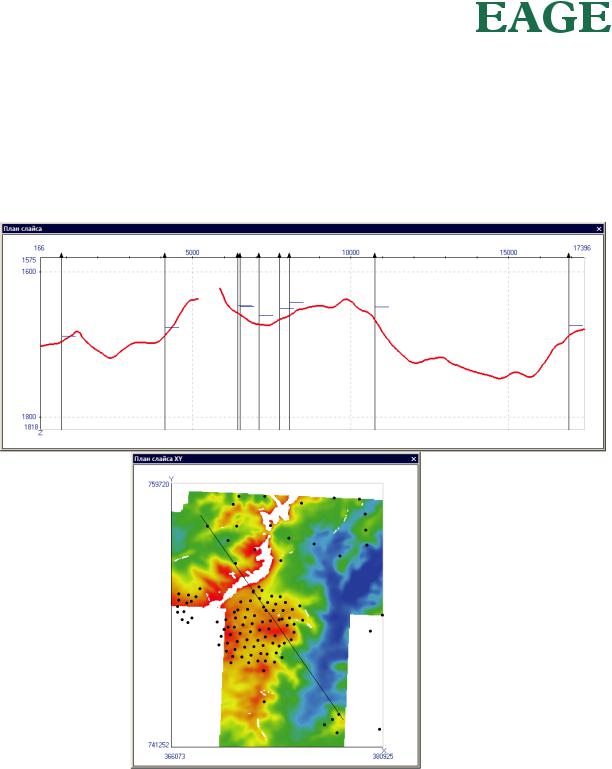
До сих пор мы рассматривали кригинг как средство интерполяции одних только точечных данных. Сейчас же мы рассмотрим, как при помощи кригинга можно интерполировать точечные данные с учетом дополнительных пространственных данных, которые мы считаем менее точными, но которые тоже могут и должны внести свой вклад в результат. С этой ситуацией мы сталкиваемся, например, когда интерполируем отметки кровли резервуара на скважинах с учетом близлежащей сейсмической поверхности (рис. 33). Или это может быть задача в пространстве 3D – например, интерполяция скважинных значений пористости с учетом куба сейсмического импеданса.

Рис. 33. Отметки кровли резервуара на скважинах и сейсмическая поверхность (карта и линия на вертикальном слайсе).

58

Учесть в процессе интерполяции дополнительные пространственные данные можно тремя способами:

•использовать пространственные данные как тренд;

•использовать пространственные данные как дрейф;

•выполнить кокригинг точечных и пространственных данных.

Что касается первого способа, то как работать с трендом мы уже говорили. Правда, мы не говорили, что в качестве тренда можно брать сейсмическую поверхность. В чем здесь особенность? Необходимо все-таки убедиться, что после вычета тренда гистограмма интерполируемых значений является гауссовской. Далее мы интерполируем не сами отметки на скважинах, а их невязки с поверхностью тренда. После интерполяции невязок прибавляем тренд к результату. На этом о тренде – все. А вот о «дрейфе» и о «кокригинге» мы поговорим подробнее.

4.1. Кригинг с внешним дрейфом (КВД)

Давайте вспомним универсальный кригинг. При интерполяции поверхности по точечным данным мы предположили, что в данных есть тренд в виде некоторой наклонной плоскости

T (x) = T (x, y) = ax + by + c

Но мы этот тренд не искали. Мы вывели систему уравнений, которая позволяет кригингу самому подобрать коэффициенты a, b и c так, чтобы сделать вариацию (7) минимальной. Обратите внимание – в результате решения системы уравнений (10) коэффициенты a, b и c мы не получили, но мы получили результат кригинга с включенным трендом (рис. 24в). При удалении от точек данных кригинг выходит на этот тренд.

Кригинг с внешним дрейфом (КВД) очень похож. Мы берем некоторую известную нам поверхность S(x,y) и предполагаем, что в наших точечных (скважинных) данных есть тренд в виде

Далее мы точно так же выводим систему уравнений, которая позволяет кригингу самому подобрать коэффициенты a0, a1 так, чтобы сделать вариацию (7) минимальной. В результате решения системы уравнений коэффициенты a0, a1 мы не получим, но мы получим результат кригинга с включенным дрейфом. То есть, при удалении от точек данных кригинг будет выходить на тренд вида (11).

Отличие дрейфа от тренда показано на рис. 34. Дрейф, в сравнении с трендом, дает кригингу больше свободы – кригинг может менять его уровень и его амплитуду. Отличия дрейфа от тренда очень важны вот в каком контексте. Коэффициенты a0, a1 можно интерпретировать как коэффициенты пересчета отражающей сейсмической поверхности из временного масштаба в глубинный. А именно, коэффициент a1 можно трактовать как эффективную скорость сейсмических волн, а коэффициент a0 - как статическую поправку. Это позволяет брать поверхность S(x,y) непосредственно из временного сейсмического куба. Использование же КВД с опцией «скользящая окрестность» позволяет учитывать изменения эффективной скорости на плане XY. То есть, опираясь (первое) на скважинные данные в отношении глубины рассматриваемой поверхности и (второе) на сейсмическую карту этой поверхности во временном масштабе, кригинг самостоятельно выполняет скоростной анализ среды.

59

Рис. 34. Отличие дрейфа от тренда. Внимательному читателю поясним, что «дыры» в сейсмической поверхности устранены посредством ручной редакции.

Что нам осталось? Нам осталось вывести систему уравнений кригинга с внешним дрейфом. Названный вывод производится аналогично выводу уравнений универсального кригинга. Отличие состоит только в том, что надо дополнительно минимизировать вариацию не по коэффициентам линейного тренда, а по коэффициентам a0, a1. Выпишем только отличающиеся фрагменты:

Дифференцируя вариацию по параметрам a0, a1 и приравнивая результат к нулю, получаем два дополнительных уравнения:

n

∑λi S(xi ) − S(x0 ) = 0

i=1

n

∑λi − 1 = 0

i=1

Обозначим эти уравнения как

ϕ1(λi ,...,λn ) = 0 ϕ0 (λi ,...,λn ) = 0

…

Результирующая система уравнений имеет вид:

60

Но обратите внимание – как и в случае универсального кригинга, ковариации Cij в этих уравнениях должны быть без дрейфа (то есть рассчитанные после того, как дрейф исключен, или по участку, где дрейфа нет).

Проведем наше традиционное экспресс-исследование. Очевидно, что если точка прогноза x0 совпадает с точкой данных x1, то прогнозное значение будет равно значению в точке данных x1. Получить асимптотику решения на бесконечности, даже когда вариограмма имеет вид «ступеньки», мне не удалось. Может быть, у вас получится. Чтобы понять, как ведет себя решение, пришлось сделать еще большее упрощение – оставить только две точки данных, x1 и x2. Решение системы в этом случае имеет следующий вид:

Мы видим, что решение воспроизводит дрейф S(x) с коэффициентом, зависящим от соотношения масштабов изменений Z(x) и S(x).

4.2. Кросс-ковариация

Давайте вспомним логику наших рассуждений о ковариации. Понятие «ковариация» мы ввели на примере двух случайных переменных Z1(x) и Z2(x). Мы сказали, что посредством ковариации будем характеризовать склонность этих переменных одновременно (при одном значении координаты x) находиться по одну сторону от своих средних:

Cov[Z1 (x), Z2 (x)] = E{[Z1 (x) − m1 ][Z2 (x) − m2 ]}

Ковариация двух случайных переменных есть просто число. Ковариация (если она имеет место) позволяет предсказывать значение одной переменной по известному значению другой. Ковариация, нормированная на среднеквадратичное отклонение Z1 и Z2, есть безразмерный коэффициент корреляции. Это был наш первый шаг.

61

Потом мы сказали, что если в качестве второй переменной Z2 брать ту же самую первую переменную Z1, но в точках с некоторым смещением h, то можно рассчитать уже не число, а некоторую функцию ковариации C(h):

C(h) = Cov[Z1(x), Z1 (x + h)] = E{[Z1 (x) − m1 ][Z1(x + h) − m1 ]}

Ковариация C(h) показывает, насколько резко меняется переменная Z1 при изменении x. Знание ковариации позволяет нам предсказывать поведение случайной переменной Z1(x) в точках, соседних с известными, то есть наилучшим образом интерполировать точечные значения Z1(x). Это был наш второй шаг.

Третий шаг, который мы сейчас сделаем, просто совмещает два предыдущих. Мы рассмотрим ковариацию двух разных случайных переменных, взятых в точках со смещением h:

C12 (h) = Cov[Z1 (x), Z2 (x + h)] = E{[Z1 (x) − m1 ][Z2 (x + h) − m2 ]}

Показанную функцию называют кросс-ковариацией случайных переменных, Z1(x) и Z2(x). Она выглядит примерно так же, как функция ковариации. С одним отличием. Если максимальное значение ковариации (после нормировки на дисперсию) равно единице, то максимальное значение кросс-ковариации (после нормировки на среднеквадратичные отклонения Z1(x) и Z2(x) ) равно коэффициенту корреляции Z1 и Z2 (рис. 35).

Рис. 35. Ковариация Z1 и кросс-ковариация Z1 и Z2. ρ – коэффициент корреляции Z1 и Z2.

62

4.3. Совместный кокригинг

Допустим, у нас есть две случайные переменные, Z1(x) и Z2(x), которые коррелируют друг с другом. Наличие корреляции Z1(x) и Z2(x) означает, что наряду с ковариацией C1(h) переменной Z1(x) мы имеем кросс-ковариацию C12(h) переменных Z1(x) и Z2(x). В этом случае при интерполяции кригингом точечных данных Z1(x) можно дополнительно использовать данные

Z2(x).

Вспомним, как мы выводили систему уравнений кригинга (пункт 3.2). Будем действовать точно так же, но используя еще и значения случайной переменной Z2(x). Оценку для случайной функции Z1(x0) в точке прогноза x0 (обозначим эту оценку Zcok(x0), индекс cok есть сокращение от «кокригинг») будем искать как взвешенное среднее от значений Z1(xi) и Z2(xj) в точках, соответственно, xi, i = 1, 2,…, n, и xj, j = 1, 2,…, m. Весовые коэффициенты обозначим как λi и μj:

Решение относительно коэффициентов λi и μj, обеспечивающее минимум вариации

Var[Zcok (x0 ) − Z1 (x0 )] = E[(Zcok (x0 ) − Z1 (x0 ))2 ] = min

называется «кокригинг».

Переменная Z2(x) обычно представляет собой сейсмический параметр, и мы можем взять ее хоть в миллионе точек. Однако, поскольку Z2(x) меняется очень плавно, то, кроме усложнения системы уравнений кокригинга (мы помним, что каждая точка добавляет одно уравнение), это нам мало что даст. Поэтому мы поступим иначе. При оценке Zcok(x0) мы будем брать вторую переменную только в одной точке x0, то есть именно в той точке, в которой мы делаем прогноз:

n

Zcok (x0 ) = ∑λi Z1 (xi ) + μ Z2 (x0 )

i=1

Это важное упрощение получило название «совместный кокригинг».

Попробуем вывести систему уравнений совместного кокригинга. Действуем так же, как и при выводе системы уравнений простого кригинга. Применяем те же обозначения. Подставляя выражение для Zcok(x0) в выражение для вариации, получим:

Var[Zcok (x0 ) − Z1 (x0 )] =

Здесь С1 обозначает ковариацию Z1(x), С2 – ковариацию Z2(x) , С12 – кросс-ковариацию Z1(x), Z2(x). Условием минимума вариации является равенство нулю производной по каждому коэффициенту

63

λi, μ. Поочередно дифференцируем выражение для вариации по λ1, λ2,.. λn, μ и приравниваем результат каждого дифференцирования к нулю. В результате получаем систему уравнений:

Ее же можно записать в матричном виде:

Эта система уравнений определяет искомые λ1, λ2,.. λn, μ. Можно видеть, что ковариация переменной Z2(x) нам не понадобилась, нам оказалась нужна только ее дисперсия С200.

Выполним относительно полученной системы наше обычное исследование. Допустим, точка прогноза x0 совпадает с точкой данных x1. В этом случае столбец правой части системы уравнений будет точно совпадать с первым столбцом матрицы коэффициентов. Решением такой системы уравнений будет λ1 равно 1, а все остальные λ2,.. λn, μ равны нулю. То есть, прогнозное значение воспроизведет значение в точке данных x1, как и должно быть.

Рассмотрим противоположный случай. Допустим, точка прогноза x0 удалена от точек данных на бесконечность. В этом случае все значения ковариации С1i0 и С12i0 обращаются в ноль:

64

После этого решение системы становится очевидным:

То есть, на удалении от точечных данных в отношении Z1(x) кокригинг определяется переменной

Z2(x):

Здесь σz1 и σz2 среднеквадратичные отклонения Z1(x) и Z2(x), а ρ – их коэффициент корреляции. Обратите внимание, правая часть (14) у нас получилась как произведение трех сомножителей – Z2,

σz1 /σz2 и ρ.

4.4. Выводы в отношении кригинга с использованием вспомогательной переменной

Асимптотика (14) позволяет нам сделать обобщающие выводы. Мы рассмотрели три возможности использования вспомогательной (сейсмической) переменной при кригинге точечных (скважинных) данных. А именно, вспомогательная переменная может использоваться как тренд (первое), как дрейф (второе) и на основе кросс-ковариации с основной переменной (третье). В чем разница между этими решениями?

Там, где у нас высокая плотность скважинных данных, разницы не будет никакой. Отличия будут только на значительном удалении от скважинных данных. Значительным мы называем удаление, которое приближается, а затем начинает превышать радиус вариограммы.

Если мы используем вспомогательную переменную Z2(x) как тренд, то решение на значительном удалении от скважинных данных будет выходить на этот тренд. То есть решение будет вести себя как первый сомножитель в правой части (14). Обыкновенный кригинг добавит к тренду Z2(x)

некоторое постоянное смещение.

Если мы будем использовать вспомогательную переменную Z2(x) как дрейф, то решение (при тех же условиях) будет вести себя как произведение первого и второго сомножителя в правой части (14). То есть КВД не принимает тренд безусловно, а умножает его на соотношение масштабов изменений Z1(x) и Z2(x).

И, наконец, если мы будем использовать вспомогательную переменную Z2(x) на основе ее кроссковариации с Z1(x), то решение будет вести себя как произведение всех трех сомножителей в правой части (14). То есть, в этом случае доверие к вспомогательной переменной обуславливается не только соотношением масштабов изменений, но и реальной корреляцией Z1(x) и Z2(x). Первое использование кокригинга для картирования пористости на основании скважинных и сейсмических данных было сделано в ставшей классической работе Филиппа Дойена (Doyen, 1988).

Нам остается только повторить замечание Оливье Дюбрула (O. Dubrule, 2003). КВД чаще используется при интерполяции структурных поверхностей, когда мы имеем все основания полагаться на времена отражающих горизонтов. Кокригинг же чаще используется при интерполяции свойств, когда связь прогнозируемого параметра и данных сейсмики не столь надежна.

65

5. Стохастические реализации

Перед тем, как сделать очередной шаг, резюмируем коротко наши достижения. В главе 2 мы выяснили суть геостатистики. Параметр геологической среды (в случае 2D это структурная поверхность, в случае 3D это куб пористости и т.п.) мы представляем в виде случайной переменной. Эту переменную мы разделяем на детерминированную часть и случайный стационарный остаток. Стационарный остаток мы характеризуем при помощи среднего значения, дисперсии и вариограммы. Вариограмму остатка мы рассчитываем по известным точечным значениям и аппроксимируем разрешенной моделью. После этого мы полагаем, что наиболее адекватным представлением рассматриваемой случайной переменной (ее стационарной части) будет бесконечный набор реализаций, каждая из которых отвечает вариограмме и воспроизводит значения в известных точках. Реальный параметр (мы так считаем) совпадает с одной из этих реализаций, мы только не знаем, с какой именно. Эти реализации позволяют нам давать ответы на очень важные практические вопросы (какие вопросы – повторять не будем).

Теперь мы знаем (после глав 3 и 4), что такое кригинг. Кригинг, по определению, это такое детерминированное решение, от которого среднеквадратичное отклонение реализаций минимально. Кригинг является оптимальным, когда нам надо дать одно единственное решение. Кроме того, мы знаем, как рассчитать кригинг, как рассчитать ошибку кригинга, насколько широкие возможности имеет кригинг в части исключения случайных (и систематических) ошибок, а также в части учета сейсмических данных.

Чего мы пока не знаем? Мы пока не знаем, как рассчитываются реализации. Мы также не знаем, с какими проблемами мы сталкиваемся при расчете реализаций. Именно об этом мы будем говорить в данной главе.

5.1. Метод последовательного гауссовского стохастического моделирования (ПГСМ)

Наиболее известным методом расчета реализаций непрерывного параметра является последовательное гауссовское стохастическое моделирование (ПГСМ). Метод ПГСМ впервые предложен в работе Deutsch and Journel, 1992.

Рассмотрим алгоритм ПГСМ. Для большей наглядности будем считать, что моделирование производится на двумерной сетке. В трехмерном случае все делается точно так же.

Итак, мы считаем, что в некоторых ячейках сетки мы имеем известные значения непрерывного параметра (рис. 36). Пусть это будет пористость, а известные значения – это значения в скважинах. Далее, когда мы будем говорить «точка на сетке», мы будем иметь в виду центр ячейки.

66