Ковалевский. Книжки по геостатистике / EAGE_Kovalevsky_SLTRU_2011_Geological_Modelling_on_the_Base_of_Geostatistics

опция ограничивает число участвующих в интерполяции точек данных. Чтобы точки данных равномерно окружали точку интерполяции, используется их отбор по квадрантам.

Шиле и Дельфинер (Chiles, Delfiner, 1999) пишут о том, что радиус окрестности желательно брать равным двойному радиусу вариограммы. Влияют на интерполируемое значение, действительно, только точки в пределах радиуса вариограммы, но сила этого влияния зависит от исходных данных в пределах радиуса вариограммы вокруг уже этих точек.

При использовании опции «скользящая окрестность» коэффициенты системы уравнений кригинга приходится каждый раз (то есть для каждой точки интерполяции) пересчитывать. Если же используется опция «глобальная окрестность» (то есть сразу все точки данных), то этого не требуется. Во втором случае пересчету подлежит только столбец правой части. Поэтому при числе точек данных менее тысячи (что обычно выполняется при интерполяции скважин) рекомендуется учитывать их все одновременно. Однако, несколько забегая вперед, скажем следующее. При расчете стохастических реализаций, когда каждая рассчитанная точка интерполяции далее рассматривается как точка данных, без опции «скользящая окрестность» не обойтись.

3.4. Стандартное отклонение кригинга

После того, как весовые коэффициенты, минимизирующие вариацию относительно кригинга, найдены, с их помощью можно рассчитать саму эту вариацию (средний квадрат отклонения реализаций от кригинга). Например, можно использовать для этого выражение (8). Удвоенное среднеквадратичное отклонение дает нам доверительный интервал, в который попадает 95% реализаций. То есть, кригинг позволяет рассчитать не только интерполяцию, минимизирующую ошибку, но и саму эту ошибку.

На рис. 25 показана карта поверхности и ассоциированная с ней карта среднеквадратичного отклонения. Это та же самая поверхность, которую мы только что рассчитали посредством обыкновенного кригинга (рис. 24б). Можно видеть, что ошибка равняется нулю в точках данных, но по мере удаления от них она постепенно возрастает. Максимальное значение ошибки равняется корню из дисперсии данных, и достигается она после того, как расстояние до ближайшей точки данных начинает превышать радиус вариограммы. На карте ошибок видно, что одна из скважин не является точкой данных – отметки уровня поверхности на ней нет, и на возможную ошибку она не влияет.

Можем ли мы считать, что если мы прибавим к поверхности кригинга удвоенную среднеквадратичную ошибку, и потом точно также ее отнимем (красная и две синие кривые на рис. 26), то мы получим возможные предельные варианты нашей поверхности? Нет, не можем. Поверхность, которую мы моделируем, не такая, как кригинг, и уж тем более не такая, как кригинг, сдвинутый на величину возможной ошибки. Кригинг (и его границы) имеет совсем не такую гистограмму, как значения поверхности в известных точках, и совсем не такую вариограмму.

47

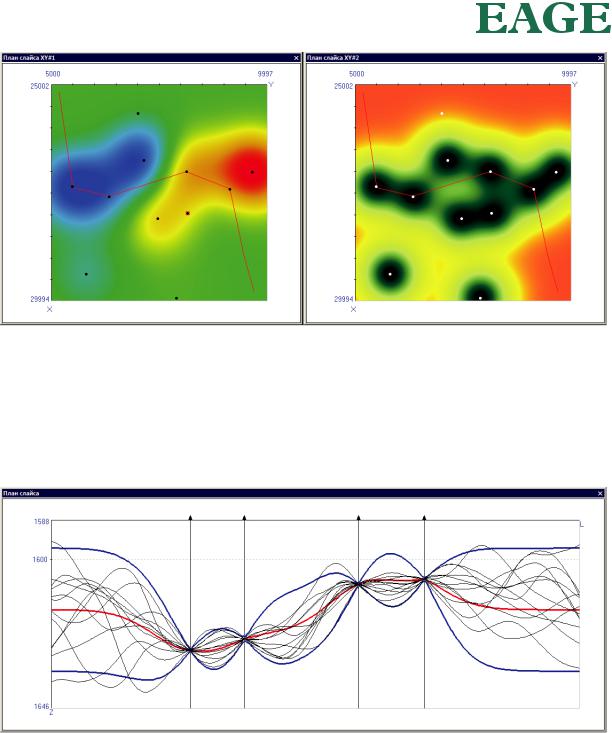
Рис. 25. Слева – карта поверхности, рассчитанной посредством обыкновенного кригинга (и показанной ранее на рис. 24б). Справа – карта соответствующей вариации (ошибки кригинга). Линия показывает сечение, см. далее рис. 26.

Еще раз, поскольку это важно – кригинг имеет совсем не такую вариограмму, как та, по которой он рассчитан. Никакого противоречия здесь нет. Кригинг дает нам не поверхность, какой она может быть, а некоторое осторожное решение, относительно которого ожидаемое отклонение нужной нам поверхности минимально.

Рис. 26. Красная линия – поверхность, рассчитанная посредством обыкновенного кригинга. Синие линии показывают удвоенную среднеквадратичную ошибку кригинга. Черные линии показывают 12 стохастических реализаций. Положение сечения показано на рис. 25.

Поверхность, которая нам нужна, может выглядеть как одна из реализаций, также показанных на рис. 26. У каждой представленной реализации и гистограмма, и вариограмма всех ее значений

48

примерно совпадают с гистограммой и вариограммой реальной поверхности, насколько мы можем судить по ее известным точкам. Но о реализациях мы будем говорить не сейчас, а позже.

3.5. Особенности кригинга, обусловленные моделью вариограммы

Рассмотрим теперь особенности кригинга, обусловленные моделью вариограммы. Поверхности, полученные при прочих одинаковых условиях (одни те же точечные данные, одинаковый радиус и порог вариограммы), но с разными моделями вариограмм, показаны на рис. 27.

Рис. 27. Поведение кригинга в окрестности точек данных. Профиль поверхности воспроизводит профиль вариограммы.

Для наглядности рассчитанные поверхности обрезаны вертикальной плоскостью, проходящей через точку данных с наивысшей отметкой. Что мы видим? Мы видим, что в окрестности точки данных профиль поверхности воспроизводит профиль начального участка вариограммы (а если точка обособлена – то профиль всей вариограммы). Наиболее плавным является отход от значения в точке данных у кригинга с гауссовской вариограммой, а наиболее резким – у кригинга с экспоненциальной вариограммой. Какую из показанных поверхностей мы должны использовать? Мы должны использовать поверхность, рассчитанную по модели экспериментальной вариограммы.

49

3.6. Перекрестная проверка

Мы только что увидели (на рис. 27), что модель вариограммы очень сильно влияет на результат интерполяции точечных данных посредством кригинга. Однако при малом количестве точек данных (особенно таких точек, которые позволяют рассчитать начальный участок вариограммы) бывает так, что мы не можем выбрать модель вариограммы уверенно (рис. 28). Как в этих условиях определить, какая интерполяция (рис. 29) лучше?

Рис. 28. При малом количестве данных подбор модели к экспериментальной вариограмме затруднен.

Существует способ контроля качества интерполяции, который называется «перекрестная проверка». Идея его очень проста. Имея, допустим, 100 точек данных, мы скрываем одну из них и выполняем интерполяцию значений по 99-ти точкам. После этого мы сравниваем интерполированное значение в скрытой точке с известным нам истинным значением в этой точке и фиксируем ошибку интерполяции (невязку), порожденную сокрытием точки. Далее мы возвращаем скрытую точку в число данных, но скрываем вместо нее какую-то другую и фиксируем ошибку интерполяции уже в этой второй точке. Выполнив поочередно данную процедуру для всех точек данных, мы получаем число невязок, равное количеству точек. Далее мы строим гистограмму этих невязок. Поскольку ошибки интерполяции случаются как в большую, так и в меньшую сторону, и поскольку большие ошибки случаются реже малых, мы получаем гистограмму, похожую на распределение Гаусса с центром около нуля (рис. 30).

50

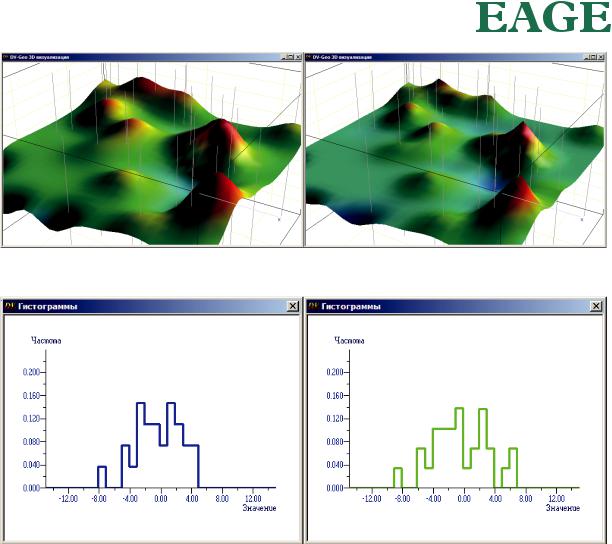
Рис. 29. Результат кригинга с гауссовской (слева) и сферической (справа) вариограммой.

Рис. 30. Результат перекрестной проверки кригинга с гауссовской (слева) и сферической (справа) вариограммой.

Затем мы таким же способом проверяем качество интерполяции другого метода и получаем вторую гистограмму невязок. Сравнив две гистограммы, мы можем однозначно определить, какой метод интерполяции лучше. Это тот метод, гистограмма ошибок которого является более узкой, то есть ошибки которого меньше, ближе к нулю. В нашем примере перекрестная проверка показывает, что результат интерполяции с гауссовской вариограммой чуть-чуть лучше.

3.7. Почему кригинг называют оптимальной интерполяцией

Теперь самое время вспомнить одну историю. Дело было в ЦГЭ лет двадцать (или уже тридцать?) тому назад. Геологические модели в то далекое время представляли собой наборы карт. Поскольку карт требовалось много, и карты были очень ответственные, была поставлена задача разработать собственную программу рисовки изолиний. Задание, как это часто в ЦГЭ бывает, поручили двум независимым группам специалистов. Обе группы задачу решили, и в назначенный день руководство получило сразу две программы рисовки изолиний.

51

Тестирование программ решили провести на одном и том же наборе точечных данных. Первая программа нарисовала идеальную карту изолиний... И вторая программа нарисовала идеальную карту изолиний... Но эти две карты оказались совершенно разными (рис. 29). В связи с этим возникло некоторое замешательство.

Рис. 29. Карты изолиний, нарисованные двумя разными программами.

Что произошло? Сама по себе рисовка изолиний, понятно, вторичная задача, главное заключается в интерполяции точечных данных. Неожиданно обнаружилось, что одни и те же данные можно интерполировать по-разному. Нет, о существовании разных методов интерполяции, конечно, знали. Неожиданностью стало то, что результаты интерполяции разными методами могут очень сильно различаться. Этот случай интересен тем, что тут мы буквально носом уперлись в геостатистику.

Что в этой ситуации дает нам знание геостатистики? Во-первых, благодаря геостатистике мы знаем, как мгновенно определить, какая из двух карт лучше. Надо для каждой карты выполнить перекрестную проверку. Та карта, для которой гистограмма ошибок будет более узкой, (допустим, это будет карта, рассчитанная программой 1) и есть лучшая. Но из этого вовсе не следует, что от программы 2 надо отказаться. Потому как на другом массиве точечных данных лучше (по той же перекрестной проверке) может оказаться карта, рассчитанная именно программой 2. То есть, геостатистика говорит нам, что у точечных данных есть некие внутренние свойства, и лучший результат (в смысле перекрестной проверки) дает тот алгоритм интерполяции, который оказывается адекватнее этим внутренним свойствам. В примере с двумя программами это происходит случайно.

Кригинг называют оптимальной интерполяцией именно потому, что прежде, чем выполнять интерполяцию, мы определяем внутренние свойства данных (рассчитываем их вариограмму) и затем выполняем интерполяцию, опираясь на эту вариограмму. Поэтому результат перекрестной проверки для кригинга всегда будет наилучшим. Пример с двумя программами рисовки изолиний очень ясно показывает суть и преимущества кригинга. Когда мне необходимо дать самое краткое и самое простое объяснение тому, что такое кригинг, я рассказываю именно эту историю.

52

Но мы должны помнить следующее. Говорить об оптимальности кригинга мы можем только тогда, когда наши данные статистически однородны.

3.8. Кокригинг ошибок и факторный кригинг

Допустим, у нас есть две случайные переменные A(x) и B(x). Это может быть полезный параметр и некоторая помеха, которая сопровождает его измерения. Пусть случайная переменная A имеет вариограмму γA, а переменная B имеет вариограмму γB. Зададим вопрос – какую вариограмму будет иметь сумма случайных переменных A(x) и B(x)?

По определению:

γ A+ B (h) = 12 E{[A(x + h) + B(x + h) − A(x) − B(x)]2}

Мы помним, что математическое ожидание E означает осреднение для всех пар точек, расстояние между которыми равно h. Перегруппируем усредняемые члены:

γ A+ B (h) = 12 E{[A(x + h) − A(x)]2} + 12 E{[B(x + h) − B(x)]2} + + E{[A(x + h) − A(x)]*[B(x + h) − B(x)]}

Перемножая скобки в последнем слагаемом, получим:

γA+ B (h) = γ A (h) + γ B (h) + E{A(x + h)* B(x + h)}+

+E{A(x)* B(x)}− E{A(x + h)* B(x)}− E{A(x)* B(x + h)}

или, если A и B не коррелируют друг с другом:

γ A+ B (h) = γ A (h) + γ B (h)

Что означает этот результат? Этот результат означает, что если наши данные включают некоторую помеху, то их вариограмма будет представлять собой сумму двух вариограмм – вариограммы полезной части и вариограммы помехи.

В чем состоит важность этого результата? Важность этого результата состоит в том, что очень часто нам гораздо легче разделить на полезную часть и помеху не сами исходные данные, а их вариограмму. Получив же вариограмму полезной части, мы можем выполнить интерполяцию именно полезной части данных, не выделяя эту полезную часть из самих данных. Для этого достаточно поставить в правую часть системы уравнений кригинга (см. например (9)) ковариацию именно полезного сигнала.

Проиллюстрируем сказанное следующим примером. Допустим, мы имеем некоторые скважинные данные. В нашем примере это отметки некоторой поверхности, но это могут быть и точечные значения пористости, и значения любого другого параметра. На рис. 31 показаны отметки на скважинах вдоль линии профиля, сама линия профиля на плане XY, а также экспериментальная вариограмма этих данных (красная кривая).

53

Рис. 31. Экспериментальная вариограмма, модели вариограммы, результаты интерполяции. На плане XY показана сглаженная поверхность.

Экспериментальная вариограмма до нуля не доходит, поскольку какое-то расстояние между скважинами всегда есть. Мы можем аппроксимировать экспериментальную вариограмму моделью, доходящей до нуля (зеленая кривая в окне вариограмм) – тогда интерполированная поверхность точно воспроизведет значения в точках данных (зеленая линия на профильном разрезе).

Но мы можем рассуждать и иначе. Мы можем предположить, что в наших данных присутствует помеха, и что экспериментальная вариограмма является суммой сферической вариограммы полезного сигнала с порогом 3.0 и вариограммы помехи в виде «ступеньки» с порогом 1.0. Решая систему уравнений простого кригинга (9), мы будем подставлять в левую часть значения ковариации суммарного сигнала, а в правую часть – значения ковариации полезного сигнала (рис. 32). При этом, в отличие от простого кригинга, если точка прогноза будет совпадать с точкой

54

данных, интерполированное значение не будет воспроизводить «зашумленное» значение в той самой точке, а будет равно некоторой сглаженной величине, рассчитанной по всей совокупности точек данных (синяя кривая на профильном разрезе на рис. 31).

Рис. 32. Кокригинг ошибок (факторный кокригинг).

Исключение описанным образом случайной ошибки в виде белого шума (с вариограммой в виде «ступеньки») называют кокригингом ошибок. Что бы выполнить кокригинг ошибок, достаточно использовать при интерполяции модель вариограммы с эффектом самородков. Отношение порога вариограммы (за вычетом эффекта самородков) к эффекту самородков можно интерпретировать как отношение «сигнал-шум». Более сложный вариант, когда описанным образом исключается систематическая ошибка с некоторой своей вариограммой (например, порожденная системой наблюдений), называют факторным кригингом.

3.9. Кригинг как рабочий процесс. О корректном применении кригинга

Подведем очередной промежуточный итог. Самое необходимое из того, что надо знать о кригинге, мы рассмотрели. Итак, кригинг – это метод интерполяции точечных данных, основанный на случайной модели среды. Получив данные (таблицу точек), мы, прежде всего, изучаем их гистограмму. При этом наша цель – обнаружить и по возможности исключить из данных детерминированную составляющую (тренды, категории, аномальные области и т.п.). Пока мы это не сделали, геостатистика не применима. Необходимый (но не достаточный) критерий отсутствия в поведении переменной детерминированных особенностей – гауссовский вид гистограммы ее значений в известных точках. При необходимости (и с учетом количества данных) на этом этапе решается вопрос о разбиении области моделирования на подобласти, в которых данные можно считать статистически однородными.

55

После гистограммы мы исследуем экспериментальную вариограмму. С помощью вариограммы мы вторично судим о стационарности данных – вариограмма должна выходить на плато. Далее мы должны убедиться, что вариограмма имеет наклонный участок, то есть что мы выявили масштаб пространственной изменчивости. Если наклонного участка нет, необходимо хотя бы локально увеличить плотность данных. Пока мы не установили, что радиус вариограммы больше нуля (и не определили этот радиус), геостатистика не применима. Дальше, рассчитывая вариограммы по азимутам, мы судим о наличии анизотропии. Этап заканчивается тем, что мы подбираем модель вариограммы.

Если точек с данными больше тысячи, принимается решение в отношении скользящей окрестности. Рекомендуется использовать окрестность с радиусом равным двойному радиусу вариограммы.

Результатами кригинга являются интерполированная карта параметра (или куб параметра в случае 3D) и карта (куб) стандартного отклонения кригинга. Если принятая модель вариограммы вызывает сомнения, выполняется расчет с разными моделями и оптимальное решение выбирается на основе перекрестной проверки.

Рассчитав кригинг, мы понимаем, что он дает нам достаточно условное представление об истинных значениях пористости на площади или о поведении структурной поверхности. При отходе от точек данных кригинг выходит на среднее – но мы не считаем, что реальная пористость тоже выходит на среднее! Гистограмма и вариограмма кригинга не такие, как гистограмма и вариограмма значений в среде. Кригинг есть осторожное решение, относительно которого средний квадрат отклонения реализаций параметра (действительно возможных значений параметра) минимален.

Но что будет, если мы в самом начале не обратим внимания на то, что гистограмма значений параметра в исходных точках негауссовская. Допустим, гистограмма пористости по скважинным данным на площади в пределах некоторого горизонта окажется двугорбой – как следствие наличия двух категорий пород. Или двугорбой окажется гистограмма отметок стратиграфической поверхности на скважинах – как следствие разлома и вертикального сдвига одной части поверхности относительно другой. Сможем ли мы в этих условиях рассчитать вариограмму данных? Да, сможем, и вариограмма может получиться очень хорошей (с наклонным участком и плато). Сможем ли мы дальше решить систему уравнений кригинга? Да, сможем, и у нас будет и карта интерполированных значений, и карта ошибок. Но что это будет за результат? Мы знаем, что кригинг, как только точки данных расходятся, тянется к среднему. А среднее у нас бессмысленное! Это или несуществующая промежуточная пористость (между коллектором и неколлектором), или столь же несуществующий промежуточный уровень поверхности (между уровнями поднятого и опущенного участков).

А что в этом случае покажут реализации? Мы сможем рассчитать реализации? Да, сможем (алгоритм расчета реализаций будет описан ниже). Реализации, как мы знаем, «крутятся» вокруг кригинга в коридоре, который определяет ошибка кригинга. И именно значение кригинга реализации принимают чаще всего (рис. 26). Если кригинг будет иметь бессмысленное значение, то и реализации будут давать нам формально правильное, но, по сути, совершенно ложное представление о среде.

Вот в этом все дело! Опасность некорректного применения кригинга (и геостатистики в целом) очень велика именно потому, что никаких формальных препятствий на этом пути мы не встречаем.

56