Ковалевский. Книжки по геостатистике / EAGE_Kovalevsky_SLTRU_2011_Geological_Modelling_on_the_Base_of_Geostatistics

Рис. 5. Стационарное поведение случайной переменной. На среднее (красная сплошная линия) и среднеквадратичное отклонение (две красные пунктирные линии) полагаться можно.

Пример нестационарной случайной переменной показан на рис. 6. Можем ли мы рассчитать для нее среднее значение и дисперсию (среднеквадратичное отклонение)? Да, можем. Но можем ли мы положиться на это средне и эту дисперсию (среднеквадратичное отклонение)? Нет, не можем. Очевидно, что прогноз на их основе является очень плохим – среднее значение почти всегда находится в стороне от значений переменной, а среднеквадратичное отклонение сильно завышает ошибку прогноза.

17

Рис. 6. Нестационарное поведение случайной переменной. На среднее (красная сплошная линия) и среднеквадратичное отклонение (две красные пунктирные линии) полагаться нельзя.

Однако ситуацию, изображенную на рис. 6, можно исправить. Для этого достаточно найти и вычесть из значений случайной переменной детерминированный тренд (голубая линия). В результате задача сводится к случаю, показанному на рис. 5, после чего точность прогноза значительно возрастает. Названное преобразование называется приведением случайной переменной к стационарному виду.

На рис. 7 показано стационарное и нестационарное поведение случайной переменной в случае 2D. Это карты стратиграфических поверхностей, но точно так же могут выглядеть и карты пористости. Важным является то, что левая карта показывает стационарное поведение переменной, а в поведении переменной, показанной в центре, присутствует некоторая неслучайная составляющая. Выделенный ее детерминированный тренд показан справа.

18

Рис. 7. Стационарное (слева) и нестационарное (в центре) поведение переменной в случае 2D. Картина справа показывает выделенный тренд.

Наряду с термином «стационарность» и в том же значении мы будем использовать термин «статистическая однородность».

2.3. Первый критерий стационарности. Анализ гистограмм

Теперь зададим такой вопрос: «Можно ли отличить стационарное поведение переменной от нестационарного не на глаз, а при помощи какого-нибудь формального критерия?» Да, можно. Не достаточным, но очень сильным критерием является вид гистограммы значений переменной. Если гистограмма значений похожа на распределение Гаусса, то, скорее всего, мы имеем стационарный (статистически однородный) случай. Если гистограмма не гауссовская, то наш случай точно не стационарный. Названный критерий используется в геостатистике постоянно.

Продемонстрируем данный критерий на примере карт, показанных на рис. 7. Гистограммы видимых значений представлены на рис. 8. Красная кривая на рис. 8 соответствует левой карте – гистограмма очень близка к гауссовской, то есть подтверждает стационарное поведение переменной, воспринимаемое визуально. Синяя кривая соответствует правой картине – гистограмма резко отличается от гауссовской, что подтверждает явно нестационарное поведение переменной. Зеленая кривая соответствует центральной картине – гистограмма сама по себе не позволяет уверенно идентифицировать нестационарное поведение, то есть визуальное восприятие оказывается точнее.

19

Рис. 8. Гистограммы значений параметра, соответствующие картам, показанным на рис. 7.

Почему в качестве критерия стационарности (статистической однородности) мы используем сравнение именно с распределением Гаусса? Чтобы объяснить это, приведем следующий пример. Допустим, вы купили на рынке большую партию (100 кг) отборных яблок. Если вы взвесите каждое яблоко с точностью до 1 г и построите гистограмму полученных весов, то вы получите распределение Гаусса (рис. 9 слева). Почему? Это закон природы. Если отклонения значений от средней величины случайны, то эти значения распределены по Гауссу.

Рис. 9. Распределение яблок по весу. Слева – выборка содержит яблоки одного сорта. Справа – выборка содержит яблоки двух сортов.

Однако нельзя исключить, что после взвешивания яблок вы получите гистограмму другой формы, например, двугорбую (рис. 9 справа). О чем это будет говорить? Это будет говорить о том, что вам продали яблоки двух сортов. То есть, негауссовский вид гистограммы тех или иных значений (веса яблок, пористости в пробах, отметок глубины некоторого горизонта и т.д.) однозначно указывает на нестационарность – на присутствие в данных некоторого детерминированного фактора.

«Случайно» негауссовская гистограмма получиться не может.

20

Геологическая среда, как и яблоки, тоже может состоять из разных сортов (типов горных пород). Поэтому двугорбые или иные негауссовские гистограммы свойств мы очень часто получаем именно по причине того, что среда состоит из пород разных категорий. В этих условиях опираться на среднее значение свойств и их дисперсию нельзя (как и в случае с трендом). Сначала необходимо разделить среду на категории. Каждая категория будет иметь свое среднее и свою дисперсию.

Анализ гистограмм, при всей его простоте, является очень мощным исследовательским инструментом. И не только в геостатистике. Можно упомянуть, что именно анализ гистограмм является весьма эффективным средством выявления фальсификаций в ходе избирательных процедур. Искусственное вмешательство – вбросы бюллетеней, приписки – мгновенно нарушает естественные (гауссовские) распределения показателей явки и числа голосов в пользу различных кандидатов или партий на множестве избирательных участков.

Подведем первый итог. Мы собираемся строить геологическую модель. В ходе этого процесса мы будем интерполировать сначала структурные поверхности, а затем значения свойств. И в первом, и во втором случае мы будем на основе точечных (скважинных) данных прогнозировать значения в пространстве некоторого параметра Z(x). При этом мы будем стараться воспроизвести истинную изменчивость геологической среды, то есть наш расчет мы будем основывать на статистических свойствах данных. Но мы только что увидели, что даже простейшим прогнозом – средним и дисперсией – можно пользоваться только в стационарном (статистически однородном) случае. Первым критерием стационарности является вид гистограммы известных значений параметра. (О втором критерии мы скажем чуть позже). Если гистограмма гауссовская – наш случай, скорее всего, стационарный, и на среднее и дисперсию полагаться можно. Если гистограмма негауссовская – у нас точно нестационарный случай, и на среднее и дисперсию полагаться нельзя. Во втором случае надо искать причину нестационарности. Это может быть или тренд (рис. 6), или наличие аномальной области, или категориальный характер среды (рис. 9) – одним словом, некоторая детерминированная черта. На среднее и дисперсию мы сможем положиться только после того, как причина нестационарности будет выявлена и исключена.

Почему мы так много говорим о возможности использовать среднее и дисперсию? Потому, что если мы не можем положиться на среднее и дисперсию, то и на все последующие геостатистические прогнозы тем более положиться будет нельзя. Сейчас мы увидим, что геостатистика добавляет к среднему и дисперсии случайной величины совсем немного, всего только одну ее дополнительную характеристику – ковариацию.

2.4. Исходное положение геостатистики

Итак, мы пришли к тому, что прогнозируемый пространственный параметр Z(x) должен быть представлен как сумма детерминированной части m(x) и случайного стационарного остатка R(x):

Названное представление называют исходным положением геостатистики.

Но ведь это очень бедное, невыразительное представление! Два простых слагаемых, первое – известная детерминированная часть, и второе – стационарный случайный остаток с известным средним и известной дисперсией. Ну и что? На чем здесь можно построить науку?

21

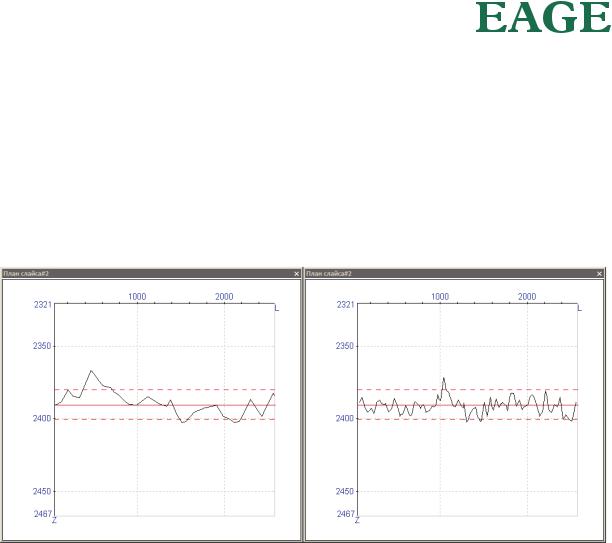
Дело в том, что стационарные случайные остатки, или лучше сказать переменные, даже при одинаковом среднем и одинаковой дисперсии, могут вести себя совершенно по-разному. То есть, помимо среднего и дисперсии, существует еще одна (третья) характеристика этих переменных, которая позволяет их различать, подробно описывать и даже предсказывать их поведение (при всей их случайности).

Третья характеристика, которую мы имеем в виду, называется ковариацией. Она показывает, как резко меняется случайная переменная вокруг своего среднего и внутри коридора, определяемого дисперсией (рис. 10). Но это мы забегаем вперед. Сначала мы напомним, что такое ковариация двух разных случайных переменных X и Y и как она связана с коэффициентом их корреляции, а затем покажем, как при помощи ковариации описывается пространственная изменчивость случайной переменной Z(x).

Рис. 10. Примеры различного поведения стационарной переменной Z(x) при одинаковом среднем и одинаковой дисперсии. Показанное различие описывается ковариацией.

2.5. Ковариация двух случайных переменных X и Y

Чтобы понять, что такое ковариация, достаточно просто прислушаться к этому слову. Это совместная, согласованная вариация (кстати, очень похоже на слово «кооперация»). Пусть у нас есть две случайные переменные X и Y, зависящие от координат в пространстве или во времени. Мы хотим определить, есть ли между случайными переменными X и Y какая-нибудь связь. Мерой этой связи является ковариация X и Y, которая обозначается Cov(X,Y). Последняя характеризует склонность двух случайных величин одновременно (при одном значении координаты) находиться по одну сторону от своих средних:

Здесь E обозначает математическое ожидание, E(X) равно среднему значению mx случайной переменной X. Осреднение идет по всем значениям координат. Соответственно, ковариация X и Y есть просто число, от координат она уже не зависит.

22

Если в формуле (2) случайные переменные ведут себя согласованно (допустим, обе склонны одновременно быть или выше своих средних, или ниже), то тогда в квадратных скобках у нас всегда будет положительная величина, которая после осреднения тоже даст величину положительную. Если же согласованности нет, то усредняться будут знакопеременные случайные величины, и результат будет близок к нулю.

Знание ковариации позволяет нам, используя одну случайную величину, предсказывать поведение другой. Допустим, X есть температура воздуха в центре Москвы, измеряемая в каждый полдень, а Y есть количество проданных в тот же день (и тоже в Москве) порций мороженного. То есть, в каждый день года мы имеем две случайные величины. Для летних месяцев их ковариация, скорее всего, будет значительной, поскольку в жаркие дни мороженного продается больше, а в холодные – меньше. Используя рассчитанное (по данным за некоторое предшествующее время) значение ковариации, директор хладокомбината сможет, ориентируясь на прогноз температуры воздуха на предстоящий день, увеличивать или уменьшать свое суточное производство. Но только летом. Для других сезонов никакой ковариации, скорее всего, не будет.

Однако ковариацию, определенную по формуле (2), трудно использовать, поскольку она имеет сложную размерность. И мы не можем сразу сказать – 10000 [порций]*[градусы], это много или мало? Для исключения названной неопределенности ковариацию нормируют на среднеквадратичное отклонение X и Y. В этом случае она превращается в хорошо всем известный безразмерный коэффициент корреляции ρ, который может принимать значения от -1 до 1.

Максимальная корреляция имеет место в случае, когда переменная коррелирует сама с собой, то есть когда Y равен X. Нетрудно видеть, что в этом случае ρ становится единицей. Значение -1 получается тогда, когда отклонения случайных переменных от их средних значений точно согласованы, но противоположны по знаку.

2.6. Ковариация случайной переменной Z(x). Вариограмма

Пусть у нас есть пространственная стационарная случайная переменная Z(x). Например, это могут быть значения пористости на некоторой площади. Ковариацию пространственной переменной Z(x) определяют как ковариацию двух случайных переменных – Z(x) и Z(x+h), то есть как ковариацию переменной с ней же самой, но взятой в точках со смещением h.

Осреднение в приведенной формуле идет по всем парам точек, расстояние между которыми равно h. Результат этого осреднения не зависит от положения пар точек в пространстве, а только от расстояния между ними. Очевидно, что Cov(Z(x), Z(x+h)) будет иметь вид некоторой спадающей функции от h. Максимальное значение ковариация будет иметь при h=0, и это значение, по определению, будет равно дисперсии Z(x). С увеличением h ковариация будет уменьшаться (согласованность поведения Z(x) и Z(x+h) будет снижаться) и, начиная с некоторого h, станет равной нулю. Примерный график ковариации Z(x) показан на рис. 11.

23

Рис. 11. График ковариации C(h) стационарной случайной переменной Z(x).

У ковариации Z(x), которую мы определили по формуле (4), есть один недостаток – при ее расчете необходимо знать еще и среднее значение mZ. В чем здесь проблема, ведь если у нас есть данные в отношении Z(x), то и среднее, казалось бы, тоже есть? Дело в том, что обычно мы имеем только среднее значение переменной в известных точках, а нам надо знать среднее значение переменной на всей области ее определения. Последнее нам, строго говоря, неизвестно. Кроме того, опираться на среднее мы можем лишь в стационарном случае, а стационарность надо еще доказать. Поэтому удобнее пользоваться несколько иной характеристикой изменчивости Z(x) – так называемой вариограммой γ(h), которая есть половина среднего квадрата разности значений в точках, разделенных расстоянием h. Вариограмму мы можем рассчитать прямо из данных:

Вариограмма γ(h) имеет вид возрастающей функции (рис. 12).

Рис. 12. График вариограммы γ (h) в случае стационарного поведения Z(x).

В стационарном случае график вариограммы является просто перевернутым графиком ковариации. Действительно, возьмем определение вариограммы, прибавим и отнимем внутри квадратных скобок среднее mz и перегруппируем члены:

24

γ(h) = 12 E{[Z (x + h) − mZ + mZ − Z (x)]2}

γ(h) = 12 E{[Z (x + h) − mZ ]2 + [Z (x) − mZ ]2 − 2[Z (x + h) − mZ ][Z (x) − mZ ]}

2.7. Расчет экспериментальной вариограммы. Модели вариограмм

Продолжим рассматривать случайную переменную Z(x). Как мы говорили, это могут быть значения пористости на некоторой площади. Очень важная деталь – на практике мы имеем значения Z(x) не на всей площади, а только в некотором количестве точек (на скважинах,

рис. 13а). Можем ли мы по отдельным точкам рассчитать вариограмму? Да, можем. Вариограмму, рассчитываемую по имеющимся (чаще всего точечным) данным, называют экспериментальной. При ее расчете и количество пар точек, и расстояния между точками в парах являются фиксированными. Легко показать, что если на площади у нас имеется N точек (скважин), то количество их пар будет (N-1)*N/2. Если мы отобразим каждую пару точек в координатах «расстояние между точками» и «половина квадрата разности значений Z в этих точках», мы получим так называемое «облако точек вариограммы» (рис. 13б). В отношении усреднения этих точек поступают следующим образом. Шкалу расстояний между точками разбивают на фиксированные интервалы, после чего усредняют значения половины квадрата разности Z для точек, попавших в один интервал. Каждое такое усредненное значение ассоциируется с центром соответствующего интервала. Усредненные точки соединяют отрезками и полученную ломаную линию называют экспериментальной вариограммой.

Рис. 13. Расчет экспериментальной вариограммы: а – исходные точки на площади; б – облако точек вариограммы и усредненные значения половины квадрата разности.

Экспериментальная вариограмма дает нам очень большой объем информации о поведении пространственной случайной переменной. Скажем больше – классическая двухточечная

25

геостатистика имеет всего два аналитических инструмента – гистограмму и вариограмму. Но с этими двумя инструментами, как мы увидим, можно сделать очень много. Определение «двухточечная» как раз и указывает на вариограмму. Разговор о гистограммах мы уже начали чуть раньше. О вариограммах мы тоже будем говорить очень много.

И прежде всего, скажем следующее. Вторым по важности (но тоже недостаточным) признаком стационарности случайной переменной Z(x) является выход ее вариограммы, начиная с некоторых h, на «плато». Напомним, первым признаком стационарности является гауссовский вид гистограммы значений.

Экспериментальная вариограмма может сильно отличаться от гладкой кривой, показанной ранее на рис. 12. Особенно велики эти различия бывают при малом количестве исходных точек данных, когда результаты усреднения в интервалах сильно разнятся. Имея это в виду, мы не придаем изломанному виду экспериментальной вариограммы большого значения и аппроксимируем ее гладкой кривой (рис. 14). При этом есть одна важная особенность – мы можем использовать только такие аппроксимирующие кривые, которые входят в перечень так называемых моделей вариограмм. Основные стационарные модели вариограмм показаны на рис. 15.

Рис. 14. Аппроксимация экспериментальной вариограммы модельной кривой.

Рис. 15. Основные стационарные модели вариограмм.

26