Ковалевский. Книжки по геостатистике / EAGE_Kovalevsky_SLTRU_2011_Geological_Modelling_on_the_Base_of_Geostatistics

Кригинг дает в точке А что-то похожее на PA = 8±1%. Принять этот прогноз мы не можем, поскольку скважинные данные однозначно указывают на отсутствие вблизи данной скважины пород с пористостью 8%. Корректный геостатистический подход требует предварительно разделить среду на категории пород, после чего выполнять интерполяцию пористости отдельно в пределах каждой категории. Трудности, которые встречаются на этом пути, мы описали в главе 5. Напомним – мы так и не смогли довести пример с реальными скважинными данными до конца. Чтобы получить решение нам пришлось использовать не очень натуральный метод «Normal Score».

Но вернемся к представлению параметра в точке A. В описанном случае может быть полезным нечеткое представление, впервые введенное Л. Заде. Согласно этому представлению прогнозируемая пористость описывается бимодальной функцией принадлежности ζ, с одним максимумом около 4%, и с другим максимумом около 12% (рис. 63 б). После разделения всего диапазона возможных значений пористости (0 – 20%) на n категорий, функцию принадлежности можно аппроксимировать ступенчатой функцией и экономно представить набором из n чисел ζ 1, ζ 2,... ζ n, 0 ≤ ζ i ≤ 1, Σζ i ≤ 1. Каждое число ζ i представляет объем свидетельств в пользу того, что прогнозируемая величина принадлежит к интервалу (категории) i. Такое представление, когда значение параметра в элементарном объеме среды определяется набором из n чисел (обычно n не более 20) будем называть нечеткой моделью (Ковалевский, 2007).

6.3.3. Порождение и суммирование свидетельств

Но откуда мы получим свидетельства ζ 1, ζ 2,... ζ n в пользу различных категорий параметра в каждом элементарном объеме среды? Для расчета свидетельств можно использовать три процедуры: (1) нечеткую трансформацию скважинных данных; (2) нечеткую трансформацию сейсмических атрибутов; (3) суммирование нечетких свидетельств по правилу Демпстера.

Что такое нечеткая трансформация скважинных данных? Каждый элементарный объем на траектории скважины (и в котором, будем считать, величина параметра является истинной) можно рассматривать как источник свидетельств в пользу имеющегося в нем значения. Можно полагать, что этот источник распространяет названные свидетельства на пространственный объем эллипсоидальной формы (рис. 64). Величина этих свидетельств уменьшается от единицы в центре эллипсоида (в самом источнике) до нуля на внешней границе эллипсоида. Радиусы эллипсоида (горизонтальный и вертикальный) определяются так, чтобы в каждую точку пространства приходили свидетельства из 10-20 ближайших источников. Много большее число свидетельств приведет (после суммирования по Демпстеру) к чрезмерному доминированию категории, преобладающей в данных. Оптимальным является горизонтальный радиус, равный среднему расстоянию между скважинами, и вертикальный радиус, равный 2-3 ячейкам объема. Радиусы вариограмм (вертикальной и горизонтальной) являются предельными расстояниями для экстраполяции свидетельств.

97

Рис. 64. Каждая точка на траектории скважины является источником свидетельства в пользу своего значения.

Вторая процедура порождения свидетельств состоит в нечеткой трансформации сейсмических атрибутов. В отличие от точек на траекториях скважин, производящих свидетельства в пользу единственной категории (присутствующей в точке), одно значение сейсмического атрибута порождает свидетельства ζ1, ζ2, ... ζn в пользу сразу нескольких категорий. Это следует из неоднозначной интерпретации каждого сейсмического атрибута. Примеров включения в нечеткую модель сейсмических атрибутов пока нет.

Все независимые свидетельства, относящиеся к одному и тому же элементарному объему, суммируются. Процедура суммирования должна удовлетворять следующим трем условиям. Первое – суммирование не должно нарушать нормировку свидетельств. То есть, после суммирования сумма итоговых компонент ζi не должна превышать 1. Второе – если какое-либо из свидетельств имеет одну компоненту, равную 1 (и все остальные равные 0, как это имеет место на траектории скважины), то оно не должно измениться после суммирования. Именно это условие не позволяет использовать арифметическое суммирование свидетельств. И третье – процедура суммирования свидетельств должна быть коммутативной, то есть ее результат не должен зависеть от порядка суммирования.

Всем трем условиям удовлетворяет суммирование свидетельств по правилу Демпстера (Gordon, Shortliffe, 1985). Проще всего объяснить это правило на примере. Пусть множество значений категориального параметра состоит из четырех категорий – a, b, c и d. Объединенное множество {a, b, c, d} обозначим Θ, пустое множество обозначим ø. Предположим, мы имеем два набора свидетельств E1 и E2:

E1: a(0.32), b(0.18), c(0.28), d(0.10), Θ(0.12);

E2: a(0.55), b (0.10), Θ (0.35).

98

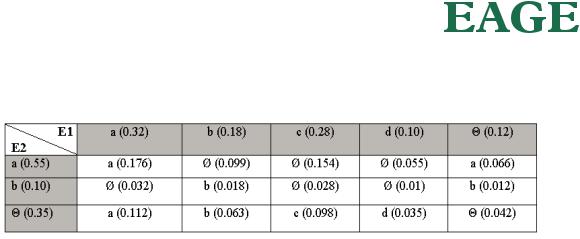
В скобках показаны свидетельства в пользу предшествующих категорий. Обратите внимание, если сумма свидетельств в пользу отдельных категорий меньше 1, остаток приписывается Θ. Для суммирования E1 и E2 мы должны составить следующую таблицу:

Табл. 1. Суммирование свидетельств E1 и E2 по правилу Демпстера.

Верхняя строка и левая колонка таблицы показывают исходные свидетельства E1 и E2. Значения в других клетках таблицы являются произведением компонент Е1 (из той же колонки) и Е2 (из той же строки). Полученные значения присваиваются категориям, которые являются пересечением категорий Е1 (из той же колонки) и Е2 (из той же строки). Пересечением одинаковых категорий и пересечением категории и Θ является та же самая категория, пересечением разных категорий является ø, пересечением двух Θ является Θ.

Величины, рассчитанные в ячейках таблицы, являются результатом суммирования. Их сумма равна 1, так что условие нормализации выполняется. Однако некоторые из рассчитанных значений присвоены ø. Мы исключаем значения, присвоенные ø, и компенсируем их потерю перенормировкой оставшихся. Объединяя разные порции свидетельств в пользу одних и тех же категорий, получим окончательный результат суммирования E3 = E1 + E2:

E3: a(0.569), b(0.149), c(0.158), d(0.056), Θ(0.068).

6.3.4. Расчет реализаций нечеткой модели

После суммирования свидетельств, исходящих из точек на траекториях скважин, мы получим искомые нечеткие представления параметра (как на рис. 63 б) в каждом элементарном объеме среды. Далее в каждом таком объеме мы сможем выявить то значение параметра, в пользу которого объем суммарного свидетельства является максимальным. Мы также сможем визуализировать эти значения параметра. При необходимости, мы сможем дополнительно рассчитать и визуализировать определенность прогноза в каждой точке среды, используя для этого, например, отношение величины максимального свидетельства к сумме всех свидетельств в той самой точке. Эти величины (параметр и его определенность) и будут результатом интерполяции скважинных данных?

Нет, не будут. Описанный прогноз не устраивает нас вот по какой причине. В нем остаются скрытыми значения параметра, в пользу которых также имеются свидетельства, уступающие максимальному, возможно, очень малую величину. Представьте – в большом объеме среды свидетельства в пользу пористости 1-2% лишь чуть-чуть превосходят свидетельства в пользу пористости 19-20%. И что же, весь этот объем мы должны записать в неколлектор? Это было бы неправильно.

Чтобы проявить скрытые (меньшие) свидетельства необходимо осуществить расчет реализаций нечеткой модели, подобно тому, как мы рассчитываем реализации методом ПГСМ. То есть, мы

99

должны обойти все элементарные объемы модели по случайному пути, исключая те, в которых значение параметра определено однозначно. В каждом очередном объеме генерируется случайное число, равномерно распределенное на интервале [0, 1]. Одновременно мы делим интервал [0, 1] на внутренние участки, пропорциональные имеющимся в этом объеме свидетельствам в пользу различных категорий. Решение о значении параметра принимается в зависимости от того, на какой участок попадает случайное число. После этого рассмотренный объем сам становится источником свидетельств в пользу той категории, которая ему определена. Заполнив весь куб, мы получим одну из множества возможных реализаций значений параметра в объеме среды. После этого мы выполняем расчет следующей реализации, начиная с выбора нового случайного пути обхода элементарных объемов, и так далее.

Важное отличие от последовательного гауссовского стохастического моделирования состоит в следующем. Если при расчете кригинга мы учтем одну точку данных 1000 раз, результат не изменится. При суммировании по Демпстеру в такой же ситуации результат изменится. Поэтому количество влияющих на очередной объем окружающих источников свидетельств должно оставаться неизменным (только 10-20 ближайших). Это означает, что радиус влияния источников по мере увеличения их числа (то есть по мере заполнения пространства определенными точками) должен сокращаться. Если этого не сделать, мы получим в 99% элементарных объемов одно и то же значение APS – то, которое преобладает в исходных данных.

Следующее замечание касается площадей с неравномерной или очень малой плотностью скважин. Максимальный горизонтальный радиус эллипсоида свидетельств не должен превышать радиус горизонтальной вариограммы, рассчитанной по скважинным данным. В противном случае на участках с малой плотностью скважин мы получим бессмысленные однородные области. Наличие предельного радиуса приводит к тому, что на большом удалении от скважин максимальным оказывается свидетельство в пользу диагноза Θ. Как мы должны поступать, когда при расчете реализаций случайное число выпадает в пользу Θ? Здесь возможны два варианта. Первый – решение можно просто откладывать (и точку не заполнять). В результате области, наиболее удаленные от скважин, будут получать значения в последнюю очередь, то есть их заполнение будет идти по мере расширения заполненных областей от скважин. Второй вариант – свидетельства в пользу Θ можно перераспределять в соответствии с гистограммой скважинных данных (или с гистограммой скважинных данных по пласту).

Множество рассчитанных реализаций нечеткой модели адекватно представляет неопределенность значений параметра в объеме среды.

100

6.3.5. Расчет реализаций нечеткой модели для примера со скважинными данными APS

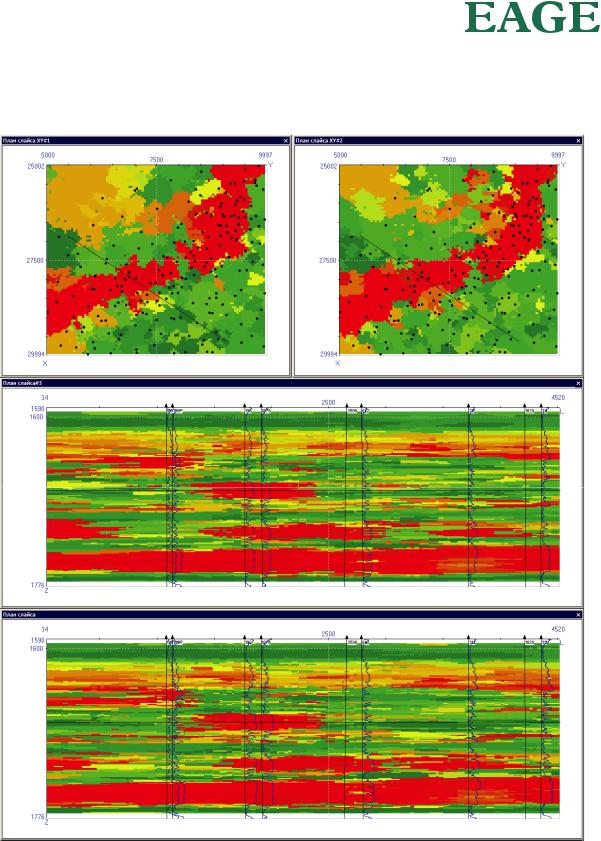
Вернемся к нашему реальному примеру. По имеющимся скважинным данным были рассчитаны две реализации нечеткой модели в отношении параметра APS (рис. 65).

Рис. 65. Вертикальное и горизонтальное сечение двух реализаций куба APS, рассчитанных как реализации нечеткой модели.

101

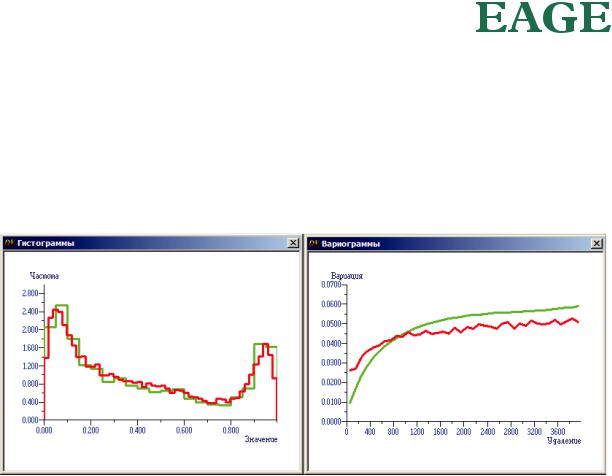
Сравнение гистограммы и вариограммы для скважинных данных и для реализации нечеткой модели показано на рис. 66. Максимальный горизонтальный радиус распространения свидетельств составлял (в соответствии с горизонтальной вариограммой скважинных данных) 750 м. Свидетельства в пользу Θ не перераспределялись, что касалось в основном только левого верхнего угла площади, где плотность скважин несколько ниже. Можно видеть, что и горизонтальная изменчивость, и гистограмма значений по скважинным данным воспроизведены в реализации нечеткой модели достаточно хорошо. Вспомним, что точно такой же результат в отношении гистограммы и вариограммы мы получили для реализации, рассчитанной методом «Normal Score» (рис. 57).

Рис. 66. Гистограммы и горизонтальные вариограммы. Красные линии – для исходных скважинных данных, зеленые линии – для реализации APS нечеткой модели.

102

6.3.6. Сравнение реализации нечеткой модели и реализации «Normal Score»

Сравним реализацию нечеткой модели с реализацией метода «Normal Score». Для наглядности поместим сечения одной и другой реализации рядом (рис. 67).

Рис. 67. Вертикальное и горизонтальное сечение реализации «Normal Score» (вверху слева и внизу) и нечеткой модели.

103

На что здесь надо обратить внимание? Первое – в реализациях метода «Normal Score» мы видим плавные переходы от больших значений параметра к малым. В реализациях нечеткой модели те же самые переходы резкие, контрастные. Второе – однородные области в реализации нечеткой модели имеют большие размеры, чем в реализации «Normal Score», поэтому реализация нечеткой модели выглядит менее хаотичной. При этом вариограммы обеих реализаций одинаковые! Что это означает? Это означает, что больший контраст значений параметра (который сам по себе ведет к более крутой вариограмме) компенсируется большим размером однородных областей (который сам по себе ведет к более пологой вариограмме). Другими словами, мы обнаружили два разных типа моделей, которые соответствуют скважинам, и которые нельзя различить по гистограмме и вариограмме. Они отличаются только характером изменения свойств. В одной модели свойства меняются резко, в другой – плавно. Но почему мы считаем, что изменения свойств в геологической среде должны быть плавными? Вопрос о том, какая из этих двух моделей ближе к реальности, остается открытым.

Но мы точно знаем, что реализация нечеткой модели не опирается на интегральные характеристики данных (гистограмму и вариограмму) и на допущение о статистической однородности среды. Строго говоря, на вариограмму расчет реализации нечеткой модели все же опирается, но очень незначительно – радиус вариограммы используется как предельный радиус экстраполяции свидетельств от скважин. Этот радиус играет очень небольшую роль и только там, где у нас малая плотность скважин. Поскольку статистические обобщения не используются, при расчете значений APS мы легко воспроизводим локальную гистограмму в каждой области и не получаем при этом никаких ложных эффектов. Сказанное подтверждается гистограммой и вариограммой реализации нечеткой модели по горизонту AV1 (рис. 68). Горизонтальное сечение реализации нечеткой модели по пласту AV1 показано на рис. 69. Оно полностью соответствует скважинным данным.

Рис. 68. Гистограммы и горизонтальные вариограммы. Красные линии – для исходных скважинных данных, зеленые линии – для реализации APS нечеткой модели. Проверка для пласта AV1.

104

Рис. 69. Сравнение реализации «Normal Score» (слева) и реализации нечеткой модели (справа) в одном и том же горизонтальном сечении пласта AV1. Цветовые палитры одинаковы. На левой картине все красные и зеленые области находятся исключительно между скважинами.

105

7. Стохастическая сейсмическая инверсия

Пусть коротко (без деления на параграфы), но мы должны рассмотреть такое важное приложение геостатистики, как стохастическая сейсмическая инверсия. Сейсмической инверсией называют задачу, когда из куба сейсмических трасс (плюс данные по некоторому числу скважин) хотят получить куб пространственных свойств – скорости Vp, Vs, импеданс, пористость и т.д. (рис. 70).

Рис. 70. Сейсмическая инверсия (Кащеев, 2011).

Главная проблема сейсмической инверсии состоит в том, что задача обращения сейсмической трассы является некорректной (в математическом смысле). Это означает, что малые (микроскопические) различия в значении амплитуды на времени T ведут к большим (огромным) различиям в значении свойств на глубине Z. В результате после инверсии двух соседних и очень похожих трасс мы получаем два сильно различающихся вертикальных разреза (импеданса или другого параметра). Мы полностью теряем горизонтальную непрерывность свойств. Понятно, что такой результат нас не устраивает. Обычные средства регуляризации решения обратной задачи (устранения некорректности) основаны на значительном понижении вертикального разрешения модели, то есть на фактическом приближении его к разрешению сейсмических данных.

Стохастическая сейсмическая инверсия позволяет обойтись без регуляризации. С ее помощью мы можем получать кубы свойств, близкие по вертикальному разрешению к скважинным данным и имеющие нужную степень горизонтальной непрерывности. Плата за высокое разрешение и непрерывность состоит в том, что вместо одного куба мы получаем много кубов (стохастических реализаций) свойств.

Рассмотрим алгоритм стохастической инверсии применительно к расчету куба импеданса. Сначала опишем исходное состояние. Первое – у нас есть куб реальных сейсмических трасс (после миграции и суммирования с сохранением амплитуд). Второе – у нас есть некоторое число скважин, на каждой из которых мы имеем вертикальный разрез импеданса, полученный с помощью каротажа. Разрезы импеданса на скважинах мы считаем точными. Третье – у нас есть стратиграфическая сетка. Вдоль слоев сетки мы рассчитываем горизонтальную вариограмму импеданса по скважинным данным (это уже четвертое). Также у нас есть вертикальная вариограмма импеданса по скважинным данным (пятое). Шестое и последнее – у нас есть форма сейсмического импульса.

106