ЛЕКЦИЯ 02_Л.А

лишь если все числа j , j 1, r нули, то есть только для тривиальной линейной комби-

нации взятых строк.

Остальные же строки в A , если таковые вообще имеются, – нулевые. Поскольку добавление нулевой строки делает систему строк линейно зависимой (свойство 4 ), то наибольшее число линейно независимых векторов в системе образов строк исходной матрицы A при преобразовании равно r максимальному количеству линейно независимых векторов в системе образов ее столбцов. Поскольку выше было доказано, что максимальное число линейно независимых столбцов в ходе преобразований сохраняется: Rg S Rg S r , приходим к естественному предположению о том, что сказанное спра-

ведливо и для строк, так что в любой матрице максимальное количество линейно независимых строк и столбцов – одно и то же.

Доказать это строго будет удобнее несколько позже, после введения важного понятия определителя (детерминанта) и изучения его свойств в качестве так называемого индикатора линейной зависимости столбцов или строк некоторой матрицы.

Примеры:

ранг и базу. Не вошедшие в базу векторы системы разложите по ней.

Реализуем описанный выше алгоритм:

Л Е К Ц И Я 1

Множество наборов чисел x1 x5 , то есть коэффициентов всевозможных линейных комбинаций векторов системы S , каждая из которых равна M 3,1 это общее решение

однородной системы линейных уравнений AX . Полагая в (2.15) x4 C1 , x5 C2 , по-

Л Е К Ц И Я 1

Иногда в обстоятельствах, подобных разбираемым, с целью некоторого упрощения конечной формулы делают однородные линейные замены одной или нескольких параметри-

что описанная картина – не частность, а общая закономерность, относящаяся к структуре решения всех вообще однородных линейных систем уравнений в случае, если часть неизвестных – параметрические.

Желая доказать линейную независимость векторов b , заметим, что их число, совпадающее с числом параметрических неизвестных, всегда равно n r , где n число неизвестных в линейной однородной системе уравнений, а r ранг системы столбцов ее матрицы A . Без ограничения общности будем считать, что параметрические неизвестные занимают последние позиции в разметочной строке после окончания прямого хода метода Гаусса.

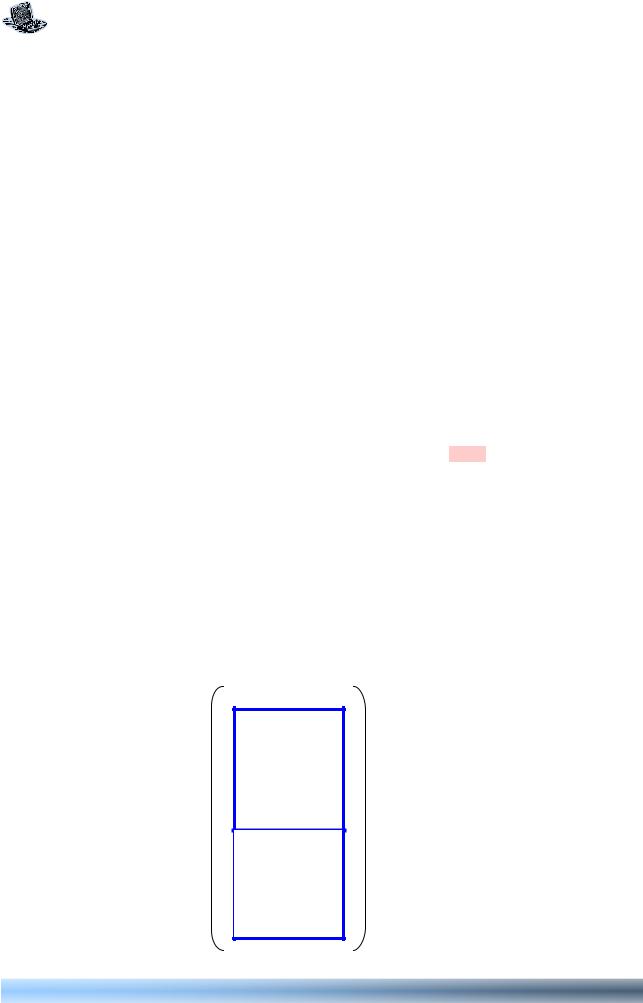
Положим n r s и выпишем покомпонентно один вслед за другим векторы

b1 , ,bs . Получившаяся матрица размеров [n (n r)] будет оканчиваться снизу единич-

ным блоком Es и имеет вид, изображенный на следующей иллюстрации

b11 b1s

bk1 bks

Es

Л Е К Ц И Я 1

Единичный блок Es стоит в матрице «во всю ширину», так что

bv . Первые k компонент линейной комбинации векторов b1 , ,bs представляют собой линейные комбинации их первых, вторых, , k х компонент с одними и теми же коэффициентами 1 , , s . Все эти линейные комбинации, очевидно, обращаются в нули при 1 s 0 .

Стало быть, только тривиальная линейная комбинация векторов b1 , ,bs может быть равна нуль-вектору, что и доказывает их линейную независимость. В своей линейной оболочке эти векторы образуют базис.

Замечание

Если векторы заданной системы S матрицы-строки, то для них задача отыскания базы, ранга и разложений по базе не вошедших в нее векторов системы решается аналогичным способом. Нужно лишь транспонировать эти строки, превратив в соответствующие столбцы, после чего следовать описанной выше процедуре.

2). Установите, является ли система векторов S {b1 , b2 , b3 }, где

26Как уже упоминалось выше, в своей линейной оболочке эти векторы образуют стандартный базис.

ЛЕ К Ц И Я 1

3). Исследуйте совместность заданной системы линейных уравнений и в случае совмест-

a). Ищем ранг системы столбцов матрицы системы (нулевые строки не отбрасывались; разметочная строка в задаче нахождения ранга системы векторов может быть опущена):

► Следовательно, Rg S A B 2 . На основании теоремы Кронеккера–Капелли заключа-

ем, что система совместна.

Л Е К Ц И Я 1

Отбросим теперь нулевые строки в последней матрице и учтем, что в процессе преобразований расширенной матрицы не пришлось менять в ней порядок столбцов (об-

ратный ход метода Гаусса здесь реализован до возникновения в зоне A единичного блока размера Rg S( A) Rg S( A B) 2 ). Получаем трапецевидную форму (2.8)’ зоны A :

что свидетельствует о наличии у системы бесконечного множества решений:

Это множество зависит от одного свободного параметра, в качестве которого возь-

мем неизвестную x3 , приняв x3 C . Выражения остальных неизвестных через пара-

метр таковы: x2 3 3x3 3 3C , x1 3 2x3 3 2C . Следовательно, решение задан-

▲ Убедитесь, что первое слагаемое в полученном выражении удовлетворяет заданной системе уравнений и поэтому является ее частным решением. Проверьте, что второе сла-

гаемое есть общее решение соответствующей однородной линейной системы, то есть сис-

темы уравнений с той же матрицей и нулевым столбцом свободных членов. Такую сис-

тему называют приведенной.

4). Решите методом Гаусса систему линейных уравнений или убедитесь в ее несовместно-

28 Говорят, что формулы, подобные полученной, определяют общее решение системы линейных уравнений, подробности в Лекции 5.

Л Е К Ц И Я 1