
SAL_chast_1
.pdf
а для второго фактора требуется учесть соответственно три варианта: |
|
|
|
t1 - ситуация, когда t зад 1 (суток); |
|
t2 |
- ситуация, когда t зад 1; 2 (суток); |
|
t3 |
- ситуация, когда t зад 2 (суток). |
|
Тогда в такой задаче при определении множества { j } необходимо учесть |
2 3 6 |
|
вариантов развития событий. А именно: |
|
|
1 - ситуация, когда одновременно реализуются события T10 и t1 ;
2 - ситуация, когда одновременно реализуются события T10 и t2 ;
3 - ситуация, когда одновременно реализуются события T10 и t3 ;
4 - ситуация, когда одновременно реализуются события T20 и t1 ;
5 - ситуация, когда одновременно реализуются события T20 и t2 ;
6 - ситуация, когда одновременно реализуются события T20 и t3 .
Сравнение альтернатив в условиях полной неопределѐнности
Проиллюстрируем особенности сравнения альтернативных решений в условиях неопределѐнности сначала следующим простым примером.
ПРИМЕР. Пусть после формализации задачи принятия решений выделено множество { j , j 1,4} из 4-х случайных событий, которые необходимо учитывать в рамках соответствующих решений. Кроме того, анализируется 5 альтернатив {X i ,i 1,5} , причем соответствующая матрица полезностей имеет вид:
Решения |
|
Доходы при событиях: |
|
|||
1 |
|
2 |
3 |
|
4 |
|
|
|
|
||||
X1 |
5 |
|
4 |
3 |
|
3 |
X2 |
6 |
|
2 |
6 |
|
4 |
X3 |
-3 |
|
6 |
2 |
|
12 |
X4 |
3 |
|
9 |
1 |
|
5 |
X5 |
7 |
|
1 |
5 |
|
3 |
Какое из этих решений следует выбрать ЛПР, если никакой другой информации (например, о вероятностях наступления событий, влияющих на экономический результат) не имеется? В частности, можно предпочесть решение X1, так как при этом решении гарантированный доход является самым большим: для любой реализации случайных событий он будет не меньше 3. Но можно предпочесть, например, решение X2 , обратив внимание на то, что только в одной из случайных реализаций (событие 2 ) это решение уступает решению X1, а в
остальных всех является более предпочтительным. Можно также предпочесть, например, решение X4, заметив, что сумма всех возможных доходов для этого решения является наибольшей. Кроме того, оптимистично настроенное ЛПР может
22
предпочесть решение X3, т.к. этому решению соответствует самый большой возможный доход (равный 12) при благоприятном стечении обстоятельств (если повезет с реализацией события 4 ). Наконец, можно предпочесть и решение X5, например, если «ожидания» ЛПР в очень большой степени связаны именно с ситуацией 1 . Как видим, можно реализовать много различных подходов при
сравнении этих альтернатив. А какое решение выберете Вы?
Для более глубокого понимания и иллюстрации соответствующих особенностей принятия решений в условиях неопределѐнности удобно выделить случай n=2, т.е. случай, когда в рамках рассматриваемой модели задачи принятия решений упрощенно допускаются только два возможных случайных события 1 и
2 , влияющих на экономический результат. Другими словами, множество { 1 , 2 } образует полную группу событий (например, 1 - благоприятные погодные условия;2 - неблагоприятные). Для такой ситуации матрица полезностей A (aij ) имеет всего два столбца. Далее элементы первого из них (относящегося к событию 1 ) будем обозначать через U i , где i – индекс соответствующего решения X i . Элементы второго столбца (относящегося к событию 2 ) обозначаем через Vi . Тогда каждое
альтернативное решение X i |
характеризуется вектором |
(U i ,Vi ) соответствующих |
||||
доходов |
при событиях 1 |
и |
2 . В соответствующем |
декартовом пространстве |
||
(U V ) |
такое решение X i |
представляется точкой (U i ,Vi ) . При этом, представляя |
||||
|
|
|
|
|||
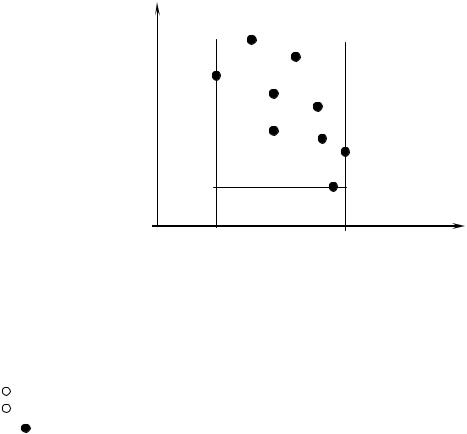
соответствующими точками все анализируемые решения |
X i , i 1, n , говорят о так |
|||||
называемом поле полезностей (см. рис. В1). |
|
|
|
|||
|
(событие 2 ) |
V |
УТ |
|
|
|
|
|
|
|
|
|
|
VУТ 
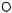
|
АУТ |
|
|
|
|
U |
|
|
UУТ |
(событие 1 |
) |
|
|
||
|
Рис. В1. Поле полезностей: |
|
|
|
- поле полезностей; |
|
|
УТ |
- утопическая точка; |
|
|
АУТ |
- антиутопическая точка; |
|
|
|
- точки, представляющие анализируемые решения. |
|
|
23
Соответствующее поле полезностей содержит все точки, представляющие
|
|
|
|
||
решения X i , i 1, n . Дополнительно выделяют так |
называемую утопическую точку |
||||
(УТ), которая соответствует условному решению |
X У , представленному вектором |
||||
доходов (UУ ,VУ ) с координатами |
|
|
|
||
|
|
UУ max U i |
и |
VУ |
max Vi |
|
|
i |
|
|
i |
Название УТ, естественно, обуславливается тем, что среди анализируемых решений {X i ,i 1, m} решения X У (как правило) не будет: иначе, не было бы необходимости
в принятии решений. Аналогично, говорят также и об антиутопической точке (АУТ), - см. рис. В1.
Выбор наилучшего для ЛПР решения (из представленных в поле полезностей) подразумевает, как минимум, необходимость сравнения имеющихся альтернатив. Сравнивая какое-либо конкретное решение, например, решение X 0 с некоторыми другими альтернативами ( X k , k 0)
возможны ситуации, которые представлены на рис. В2.
(событие 2 )
|
V |
|
|
V1 |
|
|
X1 |
|
I |
|
|
V0 |
X0 |
|
|
|
|
II |
|
V2 |
|
|
X2 |
|
|
|
U |
0 |
U0 |
U1 |
U2 (событие 1 ) |
Рис. В2. Конус предпочтений и конуса неопределѐнностей:
- конус предпочтений (для решения X 0 );
-
I и II - конуса неопределѐнностей (для решения X 0 ).
24

В частности, применительно к этому рисунку отметим, что решение X1 из конуса предпочтения (относительно X 0 ) будет для любого ЛПР предпочтительнее решения X 0 , т.к. в любой из ситуаций 1 или 2 соответствующий экономический
результат будет лучшим. Итак, все решения, для которых каждая компонента соответствующего вектора доходов из матрицы полезностей А превосходит (или равна) аналогичную компоненту решения X 0 , причем хотя бы в одной из ситуаций
j , ( j 1, n) имеет место строгое неравенство, будут предпочтительнее, чем X 0 для
всех ЛПР. Такие альтернативы называют доминирующими по отношению к решению
X 0 .
Аналогично, для всех ЛПР любое альтернативное решение из антиконуса будет хуже, чем решение X 0 , т.к. в каждой из возможных ситуаций 1 или 2 на
рис. В2 (а в общем случае – ситуаций из множества j , j 1, n ) соответствующий
экономический результат альтернативы из антиконуса предпочтений будет худшим, чем результат решения X 0 . Такие альтернативы из антиконуса предпочтений
называют доминируемым по отношению к X 0 и их можно заведомо отбросить при
нахождении наилучшего решения. Итак, все решения, для которых каждая компонента соответствующего вектора доходов из матрицы полезностей А меньше (или равна) аналогичной компоненте решения X0, причѐм хотя бы в одной из
ситуаций j , j 1, n имеет место строгое неравенство, будут заведомо худшими, чем X 0 для всех ЛПР.
Наконец, для решений из конусов неопределѐнности (I и II – на рис. В2) выбор по отношению к X 0 уже не являются очевидным и не будет одинаковым для
всех ЛПР. Например, для решения X 2 на рис. В2 соответствующий доход U 2 в ситуации 1 будет большим, чем для решения X 0 в этой же ситуации (U 2 U 0 ), но
зато соответствующий доход V2 |
в ситуации 2 |
будет меньшим, чем для решения |
X 0 (V0 V2 ) . Таким образом, |
при сравнении |
альтернатив может иметь место |
неопределѐнность (чаще всего именно так и бывает), характеризующая те особенности и затруднения, которые свойственны задачам интересующего нас типа. Каждое ЛПР реализует свои предпочтения в условиях неопределѐнности экономического результата. Поэтому выбор для различных ЛПР при сравнении решения X 0 с альтернативой из конусов неопределѐнности может оказаться
различным. Формальное задание соответствующих предпочтений для конкретного ЛПР можно реализовать на основе так называемого аппарата линий уровней.
Понятие аппарата линий уровня
Один из подходов «раскрытия» неопределѐнностей указанного типа состоит в привлечении аппарата линий уровней, характеризующих отношение конкретного ЛПР к неопределѐнности экономического результата.
Проиллюстрируем особенность такого аппарата применительно к ситуации, представленной выше на рис. В2. А именно, пусть требуется сравнить решение X 0 с
25
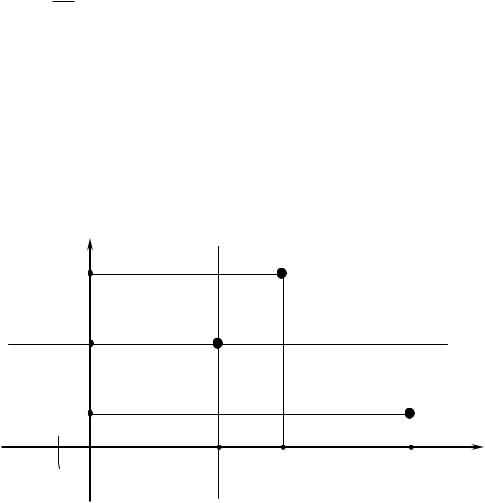
некоторой другой альтернативой (например, из области конуса неопределѐнности II), которая в ситуации 2 дает экономический результат V , худший, чем результат решения X 0 : V V0 (см. рис.В3). Другими словами, решение X 0 сравнивается с
альтернативой из области конуса неопределѐнности II, которая на рис. В3 будет представлена некоторой точкой, расположенной где-то на линии, параллельной оси
“OU” и проходящей через точку с координатами (0;V ) .
V
X 0
V0
V* |
X* |
ˆ ˆ
X ˆ
X
U 0 |
U * |
0
Рис. В3. Иллюстрация понятия линии уровня (конкретного ЛПР):
(V0 V *) |
- заданная величина потерь в случае наступления события 2 ; |
|
|||||
(U * U 0 ) |
- требуемая ЛПР компенсация соответствующих возможных |
|
|||||
|
потерь в случае наступления события 1 ; |
|
|
|
|||
X * |
- альтернатива, эквивалентная решению X 0 ; |
|
|
||||
|
- линия уровня, представляющая все точки, для которых |
|
|||||
|
соответствующие |
альтернативы |
эквивалентны X 0 |
(в рамках |
|
||
|
предпочтений конкретного ЛПР). |
|
|
|
|
||
Возможные ситуации, связанные с таким сравнением охарактеризуем |
|||||||
следующим образом. С одной стороны, очевидно, что в «крайнем» |
случае, когда |
||||||
такая альтернатива, сравниваемая с |
X 0 , |
будет |
представлена |
точкой |
ˆ |
||
X |
|||||||
(принадлежащей в этом крайнем |
случае |
антиконусу |
по отношению к X 0 ), |
то |
|||
решение X 0 |
|
|
|
|
ˆ |
|
|
будет предпочтительнее указанной альтернативы X для всех ЛПР из- |
|||||||
за потерь величины (V0 V *) в случае наступления события 2 . С другой стороны, |
|||||||
|
|
|
|
ˆ |
|
|
|
|
|
|
|
ˆ |
(см. рис. В3), лежащая на |
||
для любого ЛПР всегда найдется такая «своя» точка X |
|||||||
|
|
|
|
|
|
|
26 |
указанной выше линии, что соответствующая ей альтернатива будет для конкретного ЛПР предпочтительнее, чем решение X 0 за счет хорошей ожидаемой в
случае наступления события 1 компенсации потерь, указанных применительно к случаю наступления события 2 . Следовательно, если предпочтения ЛПР задаются
им корректно (т.е. соответствующее отношение предпочтений является
транзитивным или, по крайней мере, не допускает циклов), то между точками X и
X найдется единственная точка X , лежащая на указанной выше линии (на рис. В3 она выделена белым кружком), которая характеризуется следующими положениями.
1.Любая другая альтернатива, представленная точкой на указанной линии, расположенной левее, чем X , будет для данного ЛПР худшей, чем решение X 0 .
2.Любая другая альтернатива, представленная точкой на указанной линии, расположенной правее, чем X , будет для данного ЛПР лучшей, чем решение X 0 .
Таким образом, для любого решения X 0 при его сравнении с альтернативой
из конуса неопределѐнности всегда найдѐтся эквивалентная альтернатива в конусе неопределѐнности, причѐм такая, что для данного ЛПР реализуется ―баланс‖ между
возможной потерей (v |
0 |
v ) в случае наступления неблагоприятного события ( |
2 |
) |
|||||
|
|
|
|
|
|
|
|
||
и требуемой этим ЛПР соответствующей минимальной компенсации (u |
0 |
u ) |
|
в |
|||||
|
|
|
|
|
|
|
|
|
|
случае наступления благоприятного |
события ( 1 ) . Наконец, поскольку |
|
здесь |
|
в |
||||
наших рассуждениях величина v |
была произвольной, то эквивалентные по |
||||||||
отношению к X |
0 |
альтернативы для данного ЛПР, аналогичные X , имеются при |
|||||||
|
|
|
|
|
|
|
|
|
|
любом значении v . Соединяя все такие эквивалентные (по отношению к решению X 0 ) точки получаем линию, представляющую одну из линий уровней для данного
ЛПР: все точки на этой линии эквивалентны X 0 в рамках предпочтений этого ЛПР. Наконец, отметим, что точка X 0 в наших рассуждениях, приведѐнных выше,
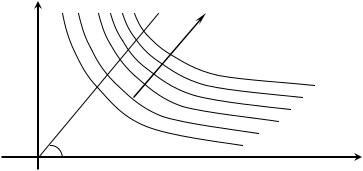
также была произвольной в пространстве (u v) . Поэтому можно говорить о семействе таких линий уровня применительно к конкретному ЛПР, не привязываясь к отдельному решению X 0 (см. рис. В4). При этом все решения, лежащие на одной и
той же линии (линии данного уровня) являются эквивалентными между собой для данного ЛПР. Кроме того, чем дальше от начала координат проходит линия, тем более предпочтительные решения она представляет: для иллюстрации сравните точки пересечения указанных линий уровня с биссектрисой первого координатного угла и дайте соответствующую интерпретацию.
событие 2 |
v |
направление |
|
||
|
|
предпочтений |
|
|
ЛПР |
0 |
450 |
u |
|
событие 1
Рис. В4. Семейство линий уровня для ЛПР.
27
На формальном уровне соответствующее семейство линий в двумерном пространстве (u v) задают на основе параметрического задания таких линий
уровня.
А именно, под линией уровня K понимают линию, определяемую соотношением
f (u;v) K ,
где
K – параметр, характеризующий отдельную линию семейства;
f (u;v) - функция двух переменных, определѐнная в пространстве (u v) и
характеризующая отношение ЛПР к неопределѐнности экономического результата, причѐм задаваемая таким образом, чтобы большим значениям K соответствовали линии уровня из этого семейства с большим предпочтением для данного ЛПР.
Таким образом, на формальном уровне задача оптимального выбора решения в условиях неопределенности применительно к двумерному пространству (u v) , т.е. для случая, когда экономический результат решения зависит от двух возможных случайных событий { 1 и 2} , может быть представлена как следующая задача
оптимизации:
f (u;v) max .
{Xi}
Окончательно, в общем случае, когда модель задачи принятия решения в условиях неопределѐнности учитывает произвольное число возможных случайных
|
|
|
|
|
|
|
событий |
{ j , j |
1, n} , влияющих на экономический результат, соответствующая |
||||
задача |
выбора |
|
наилучшего решения из заданного множества альтернатив |
|||
|
|
|
||||
{Xi ,i 1, m} представляется в виде следующей задачи оптимизации: |
||||||
|
|
|
|
|
|
f (u;v;...; z) max , |
|
|
|
|
|
|
{Xi} |
где f (u;v;...; z) |
- функция n переменных, аргументом которой являются n -мерные |
|||||
векторы-строки соответствующей матрицы полезностей. При этом указанная функция задаѐтся таким образом, чтобы ―линии уровня K‖ (в n -мерном пространстве это – соответствующие гиперплоскости), определяемые равенством
f (u;v;...; z) K ,
при больших значениях параметра K соответствовали более предпочтительным решениям для конкретного ЛПР. В противном случае (например, для матрицы рисков или потерь) решается аналогичная задача минимизации.
При нахождении наилучшего решения при заданном семействе ―линий уровня‖ (т.е. при заданной критериальной функции f f (u;v;...; z) ) удобно поступать следующим образом. А именно, к матрице полезности дописывают
28
дополнительный столбец, элементы которого ( Ki - для решения X i ) определяются по соответствующей функции f для каждой строки-решения соответствующей
матрицы. Полученные таким образом элементы дополнительного столбца как раз и характеризуют соответствующие ―линии уровня‖ для анализируемых решений. Таким образом, по этому дополнительному столбцу далее остаѐтся выбрать наилучшее решение.
Классические критерии принятия решений в условиях неопределенности
К классическим критериям указанного типа традиционно относят следующие:
максиминный критерий;
оптимистический критерий;
нейтральный критерий;
критерий Сэвиджа.
Приведѐм кратко основные характеристики и соответствующие определения для этих критериев принятия решений в условиях неопределѐнности.
1. Максиминный критерий (ММ-критерий или критерий Вальда).
Этот критерий характеризуется крайней осторожной или, как говорят, крайней пессимистической позицией отношения ЛПР к неопределѐнности экономического результата. В рамках такого подхода при сравнении альтернативных решений за основу принимается их соответствующие самые неблагоприятные результаты для возможных ситуаций развития ―внешних‖ событий, не зависящих от ЛПР, при анализируемом решении. Соответственно, в рамках такого подхода функция, задающая семейство ―линий уровня‖ определяется равенством:
f (u;v;...; z) min{u;v.;..; z}.
Применительно к обозначениям, принятым ранее для матрицы полезностей задача нахождения наилучшего решения при этом критерии формализуется следующим образом. Пусть
i– вариант возможного решения ЛПР (i 1,2,..., m);
j– вариант возможной ситуации ( j 1,2,..., n);
aij – доход ЛПР, если будет принято решение i, а ситуация сложится j-ая; A (aij ) – матрица полезностей.
Целевая функция критерия:
Z MM |
max{Ki }, где Ki min{aij } |
|
|
i |
j |
29
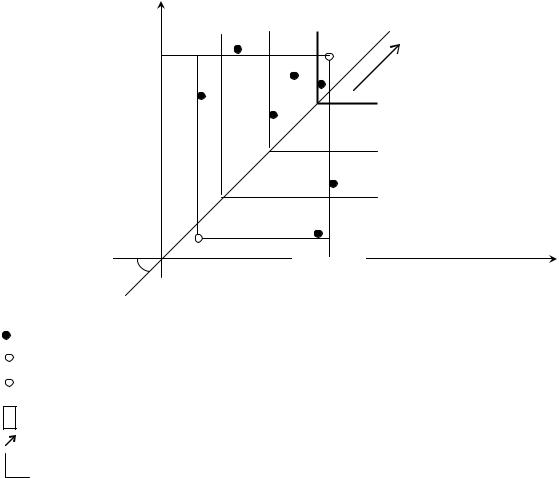
Графическая интерпретация и линии уровня критерия (n = 2)
Доход V (при j=2)
V maxmax{ }
V i j i{2ai2}
АУТ
450 
Рис 1.1. Линии уровней ММ-критерия:
УТ
max
U max{ai1} U maxi {aij} i
|
- точки возможных решений ЛПР; |
УТ |
- утопическая точка; |
АУТ |
- антиутопическая точка; |
|
- область поля полезностей; |
max |
- направление предпочтений; |
|
- линия уровня ММ-критерия. |
Доход U (при j=1)
ЗАМЕЧАНИЕ. Выбор на основе ММ-критерия обеспечивает максимальное значение величины гарантированного дохода (т.е. дохода в случае самого неблагоприятного из вариантов ―внешних‖ условий).
2.Оптимистический критерий (или H-критерий).
Этот критерий характеризуется крайней оптимистической позицией отношения ЛПР к неопределѐнности экономического результата, т.е. позицией ―азартного игрока‖, уверенного в том, что ему должно повезти, и поэтому склонного к самым рискованным выборам. В рамках такого подхода при сравнении альтернативных решений за основу принимаются их соответствующие самые благоприятные результаты среди возможных ситуаций для ―внешних‖ событий, не зависящих от ЛПР. Соответственно, в рамках такого подхода функция, задающая семейство ―линий уровня‖ определяется равенством:
f (u;v;...z) max{u;v.;..; z}.
Применительно к обозначениям, принятым ранее для матрицы полезностей задача нахождения наилучшего решения при этом критерии формализуется следующим образом.
30
|
Пусть |
||
i |
– вариант возможного решения ЛПР (i 1,2,..., m); |
||
j |
– вариант возможной ситуации ( j 1,2,...n); |
||
|
aij – доход ЛПР, если будет принято решение i, а ситуация сложится j-ая; |
||
|
A (aij ) – матрица полезностей. |
||
|
Целевая функция критерия: |
||
|
|
Z Н max{Ki } , где |
|
|
|
i |
|
|
|
Ki max{aij } |
|
|
|
j |
|
|
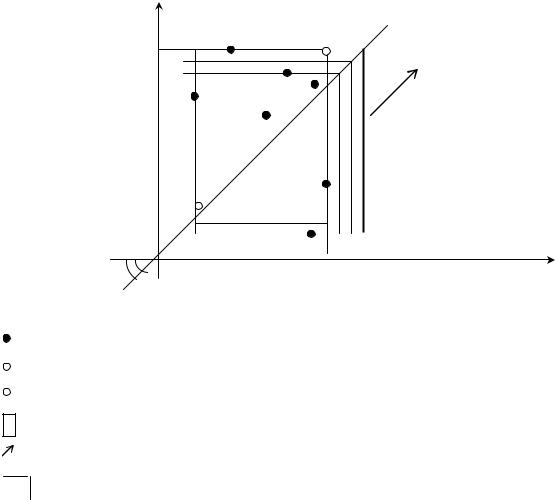
Графическая интерпретация и линии уровня критерия (n = 2) |
||
|
Доход V |
||
|
(при j=2) |
||
|
V max{ai2} |
УТ |
|
|
|
|
|
|
i |
||
|
|
|
max |
АУТ
Доход U
450 |
U max{ai1} |
(при j=1) |
|
i |
|
Рис 1.2. Линии уровней Н-критерия:
- точки возможных решений ЛПР;
УТ - утопическая точка;
АУТ - антиутопическая точка;
- область поля полезностей; max - направление предпочтений;
- линия уровня Н-критерия.
31
