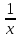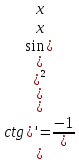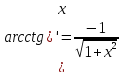- •2. Линейные операции над матрицами. Нулевая матрица.
- •3.Нелинейные операции над матрицами. Единичная матрица.
- •4.Определители. Вычисление определителей 1го, 2го и 3го порядков.
- •5)Минор.Алгебраическое дополнение.Вычисление определителя «n» - ого порядка
- •6)Свойства определителей:
- •7. Обратная матрица. Построение обратной матрицы.
- •9) Методом Крамера возможно решать только квадратные системы линейных уравнений.
- •10) Матричная запись системы:
- •16. Линейные операции над векторами в аналитической форме
- •17. Орты. Понятие базиса. Разложение векторов по базису. Линейное пространство векторов.
- •22. Множество, подмножество. Универсальное множество, пустое множество.
- •25. Биекция
- •27. Способы задания числовых функций
- •29. Таблица элементарных функций
- •30. Размерность области определения, области значения, геометрического образа:
- •36.Классификация неопределённостей.
- •37. Методы раскрытия неопределённостей
- •38. Непрерывность функции в точке, классификация разрывов
- •39. Определение производной функции. Пример вычисления производной по определению.
- •40. Таблица производных.
37. Методы раскрытия неопределённостей
[
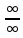 ]
]
Правило Лопиталя
Деление на самую быстрорастущую функцию:
Во всей дроби найти самую быстрорастущую ф-ю и взять ее без коэффициента
Разделить и числитель и знаменатель на это функцию
Применить свойства пределов и св-ва величин бесконечно больших и бесконечно малых
В результате раскрытия
неопределённости [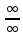 ]может
получиться либо 0, либо сonst
либо
∞.
]может
получиться либо 0, либо сonst
либо
∞.
[
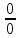 ]
]
1ый Замечательный Предел(используется при наличии тригонометрических функций в выражении)
Разложение на множители
Правило Лопиталя
1ый Замечательный Предел
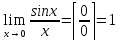
Необходимо отслеживать:
sin
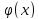 делиться точно на свой аргумент
делиться точно на свой аргумент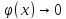
Разложение на множители
Методы:
общий множитель за скобку
использовать формулы сокращенного умножения
разложение на множители квадратного трехчлена
домножение до формулы сокращенного умножения
Идея: выделение множителей так, чтобы бм величину выделить и сократить
[∞-∞]
Случаи:
Хотя бы 1 дробь в выражении-приводим к общему знаменателю, получаем дробь, которая может дать
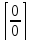 и [
и [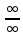 ]
]Оба целые - домножаем до формулы сокращенного умножения:
a-b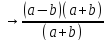
Важно:
Если степени старшего коэффициента при старшем члене одинаковы во всём выражении - можно сразу просто домножать до формулы
Если разные и степени, и коэффициенты - старшее слагаемое с коэффициентом - за скобку
38. Непрерывность функции в точке, классификация разрывов
Определение.
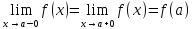
Если выполняются все равенства - функция непрерывна в точке x=a.
Если не выполняется хотя бы одно равенство - образуется разрыв.
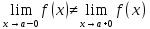 -предел
слева не равен пределу справа, оба
значения функции в точке конечны(числа)-РАЗРЫВ
1-ГО РОДА
-предел
слева не равен пределу справа, оба
значения функции в точке конечны(числа)-РАЗРЫВ
1-ГО РОДА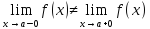 -
предел слева не равен пределу справа,
но хотя бы один одностронний предел
бесконечен –РАЗРЫВ 2 РОДА
-
предел слева не равен пределу справа,
но хотя бы один одностронний предел
бесконечен –РАЗРЫВ 2 РОДА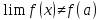 -УСТРАНИМЫЙ
РАЗРЫВ
-УСТРАНИМЫЙ
РАЗРЫВ
39. Определение производной функции. Пример вычисления производной по определению.
f’ =
 [C
; 0
[C
; 0
Производная функции равна пределу отношения приращения функции к вызывающему его приращению аргумента, если он существует и конечен.
Пример: (
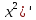 = 2x
= 2x
x
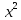
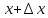
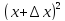
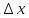
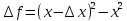
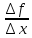 ==
==
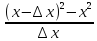
(
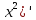 =
=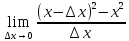 = [
= [ ]
]
(
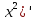 =
=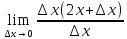 =
=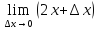 =
2x
=
2x
40. Таблица производных.
|
(С)’ = 0 |
|
|
|
( |
|
|
|
( |
|
|
|
|
|
|

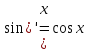
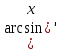 =
=
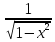
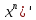 = n
= n
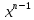
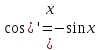
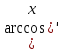 =
=
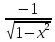
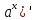 =
=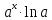
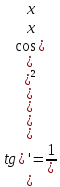
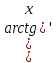
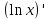 =
=