25. Биекция

При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством.

Биективное отображение называют ещё взаимно-однозначным отображением.

26. Функция - это отображение (A,B,f), где множество В - числовое

( А - область определения (любая), В - область значения(числовая) )

Пример

А - 28 студентов

В - N числа от 1 до 28

f - расположение студентов по алфавиту

(A, B, f) - биективная тройка

(A, B, f) где В - числовое множество - это функция

(A, B, f) где А и В числовые - числовая функция

27. Способы задания числовых функций

1) Аналитический способ - формула

2) Графический способ - геометрический образ

3) Таблица

(Аналит и граф способы содержат одинаковую информацию, а в таблице невозможно пересчитать все числа)

28. Аналитические способы задания функции (функция одной переменной)

1) Явное задание

y = f(x)

2) Неявное задание

f(x;y)=0

x²+y²=1

(x-a)²+(y-b)²=R²

x²/a² + y²/b²=1

29. Таблица элементарных функций

Алгебраические функции	Тригонометрические функции	Обратные тригонометрические
Линейная y = kx + b	y = sinx	y = arcsinx
Степенная y = xn	y = cosx	y = arccosx
Показательная y = ax	y = tgx	y = arctgx
Логарифмическая y = log­a­x	y = ctgx	y = arcctgx

30. Размерность области определения, области значения, геометрического образа:

Для функции одной переменной

(A,B,f)

A ⊂ R

B ⊂ R

Геом. образ ⊂ R²

Для функции двух переменных (z = 2x - y²)

(A,B,f)

A ⊂ R²

B ⊂ R

Геом. образ ⊂ R³

Для функции трех переменных

(A,B,f)

A ⊂ R³

B ⊂ R

Геом. образ ⊂ R⁴

Для функции n переменной

(A,B,f)

A ⊂ Rⁿ

B ⊂ R

Геом. образ ⊂ Rⁿ⁺¹

31. Линейная функция - функция вида у = kx + b.

Аналитические задания линейной функции: явное/неявное

Исследование общего урия:

Ax+by+cz+d=0

Свободный член равен 0, то прямая проходит через начало координат.

Если в аналитич. Задании отсутствует одна из координат, то у геометрического образа есть параллель оси с именем отсутствующей координаты.

32. Степенная функция (y=x^n)

• Парабола y=x^2; зт. (1;1)

• Гипербола y=1/x; зт (1;1) x=0 и у=0 – асимптоты

• У=х^3 зт (1;1)

• У=1/х^2 зт(1;1) х=0 у=0 – асимптоты

• У=корень из х. зт (1;1)

• У=куб. корень из х. зт 11

33. Показательная ф-я y=a^x

Логарифмическая функция

34. Функция y=sinx y=cosx

T= 2

35. Функции y=tgx y=ctgx

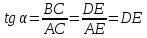
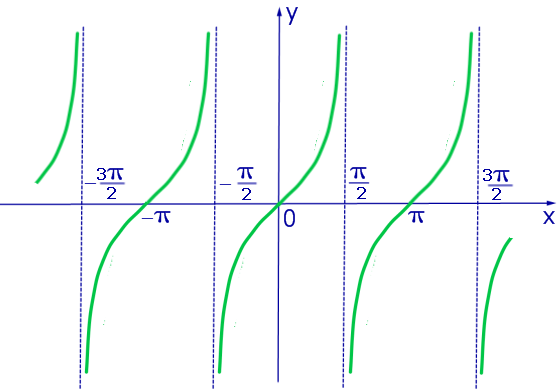
36.Классификация неопределённостей.

Если работают 2 и более функций, то возникают неопределенности.

1. Limf+limg=Lim(f+g)

Limf limg	0	c	∞
0	0	c	∞
c	c	c	∞
∞	∞	∞	∞

Действие сложения неопределённости не даёт.

2. Lim(f-g)=Limf-Limg

Lim f Lim g	0	C	∞
0	0	c	∞
c	-c	c	∞
∞	-∞	-∞	?

Действие вычитания даёт неопределённость [∞-∞]

3. Lim(f*g)=Lim f* lim g

Limf Limg	0	c	∞
0	0	0	?
c	0	c	∞
∞	?	∞	∞

Действие умножения даёт неопределённость [∞*0]

4. Lim(f/g)=

Lim f Lim g	0	c	∞
0	?	∞	∞
c	0	c	∞
∞	0	0	?

Действие деления даёт неопределённость []и [].[∞*0] и []равнозначны