|
Вопрос
7.Свойства определённого интеграла.
-
Пусть
функции f(x)
и g(x)
интегрируемы на отрезке [a,b].
Тогда функции f(x)
± g(x)
также интегрируемы на отрезке [a,b],
причем:
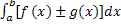 =
= 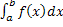 +
+ 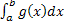 . .
-
Если
функция f(x)
интегрируема на [a,b],
то функция c·f(x),
(c=const)
интегрируема на этом отрезке, причем:
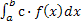 = c·
= c·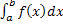 . .
-
Пусть
функция f(x)интегрируема
на отрезках [a,c]
и [c,b],
a<c<b.
Тогда функция интегрируема на отрезке
[a,b],
причем:
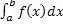 =
= 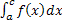 +
+ 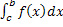 . .
-
Пусть
функции f(x)
и φ(x)
интегрируемы на отрезке [a,b]
и удовлетворяют условию f(x)
≤ φ(x).
Тогда:
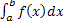 ≤
≤ 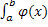 . .
-
Пусть
m
– наименьшее, а М – наибольшее значения
функции f(x)
на отрезке [a,b].
Тогда:
m(b-a)
≤ 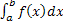 ≤ M(b-a).
≤ M(b-a).
-
Теорема
о среднем Пусть функция f(x)
непрерывна на отрезке [a,b].
Тогда на этом отрезке найдётся точка
c,
такая , что справедливо равенство:
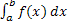 = f(c)
·(b-a).
= f(c)
·(b-a).
Доказательство:Пусть
m
,M
– наименьшее и наибольшее значения
f(x)
на отрезке [a,b],
существующие по 1ой теореме Вейерштрасса.
По
свойству 5) m
≤ 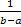
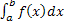 ≤
M ≤
M
Обозначим
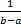
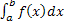 =
µ. =
µ.
Так
как f(x)
непрерывна на [a,b],
то по 2ой теореме Больцано-Коши, она
принимает промежуточное значение µ
в некоторой точке C
отрезка [a,b],
такое, что
µ
= f(c), т.е.
f(c) = 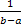
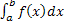 или или
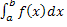 = f(c) · (b-a).
= f(c) · (b-a).
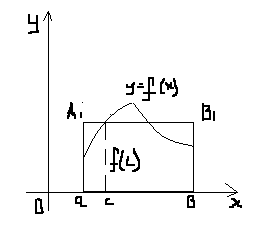
Рис.5
Если
f(x)
≥ 0 на отрезке [a,b],
то рис.5 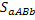 =
= 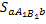 ,
площадь криволинейной трапеции aABb
равна площади прямоугольника a ,
площадь криволинейной трапеции aABb
равна площади прямоугольника a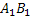 b
с тем же основанием и с некоторой
средней ординатой f(c)
в качестве высоты. b
с тем же основанием и с некоторой
средней ординатой f(c)
в качестве высоты.
|
Вопрос
8.Определенный интеграл с переменным
верхним пределом.Пусть
функция f(t)
интегрируема на отрезке [a,b].
Возьмем 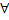 x
x
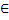 [a,b].
По свойству
[a,b].
По свойству 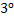 интегрируема и на отрезке [a,х].
Подсчитаем
интегрируема и на отрезке [a,х].
Подсчитаем 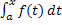 .
Это будет некоторое число, равное
площади криволинейной трапеции aAXx
(рис.6). .
Это будет некоторое число, равное
площади криволинейной трапеции aAXx
(рис.6).
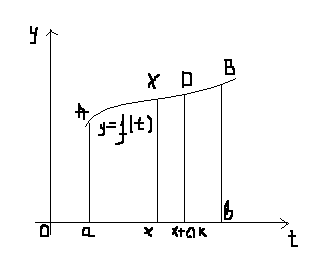
Рис.6
Таким
образом 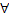 x
x
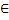 [a,b]
ставится в соответствие число
[a,b]
ставится в соответствие число 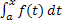 ,
которую называют определённым
интегралом с переменным верхним
пределом. ,
которую называют определённым
интегралом с переменным верхним
пределом.
Теорема.
Пусть
функция f(t)непрерывна
на отрезке [a,b].
Тогда функция F(x)
имеет производную в каждой точке x
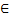 [a,b],
причем
[a,b],
причем
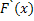 = =
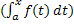 (2.8)
(2.8)
Доказательство.
Дадим аргументу приращение 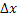 и подсчитаем приращение функции
и подсчитаем приращение функции 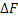 . .
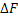 =F(x+ =F(x+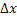 )-
F(x)= )-
F(x)=
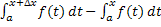 . .
По
свойству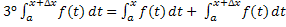 . .
По
теореме о среднем (свойство 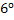 )
найдется точка с )
найдется точка с 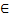 [x;
x+
[x;
x+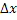 ],
такая что ],
такая что
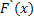 = =
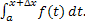
Составим
разностное отношение 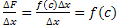
Тогда
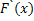 = =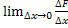 =
= 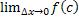 =
= 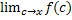 = f(x)
в силу непрерывности f(x)
на [a,b].
= f(x)
в силу непрерывности f(x)
на [a,b].
Таким
образом, мы доказали утверждение,
сформулированное в главе 1 о том, что
для непрерывной на отрезке [a,b]
функции f(x)
всегда существует первообразная;
примером её является определённый
интеграл с переменным верхним пределом
F(x)=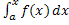 . .
Формула
Ньютона-Лейбница.Теорема. Пусть Ф(х)
– какая-либо первообразная для
непрерывной функции f(x)
на отрезке [a,b].
Тогда справедлива формула:
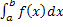 = Ф(b)
– Ф(a)
= Ф(x)
= Ф(b)
– Ф(a)
= Ф(x)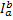 .
(2.9) .
(2.9)
ДоказательствоДля
непрерывной на отрезке [a,b]
функции f(x)
интеграл F(x)
= 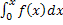 является первообразной функцией.
Зная, что разность между двумя
первообразными равно постоянному
числу. Т.е. F(x)
– Ф(x)
= C.
Чтобы определить C,
положим здесь x
= a
и учтем, что F(a)
= 0. Тогда 0 – Ф(а) = С или С = -Ф(а). При
х = b
получим F(b)
=
является первообразной функцией.
Зная, что разность между двумя
первообразными равно постоянному
числу. Т.е. F(x)
– Ф(x)
= C.
Чтобы определить C,
положим здесь x
= a
и учтем, что F(a)
= 0. Тогда 0 – Ф(а) = С или С = -Ф(а). При
х = b
получим F(b)
= 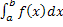 = Ф(b)
– Ф(a).Формулу
(2.9) называют формулой Ньютона-Лейбница.
Она устанавливает, что значение
определенного интеграла равно разности
двух значений любой первообразной
функции – значению в верхнем пределе
интеграла и значению в нижнем пределе
интеграла.
= Ф(b)
– Ф(a).Формулу
(2.9) называют формулой Ньютона-Лейбница.
Она устанавливает, что значение
определенного интеграла равно разности
двух значений любой первообразной
функции – значению в верхнем пределе
интеграла и значению в нижнем пределе
интеграла.
|



