5

5. Опорные решения. Отыскание исходного опорного решения

Опорным решением системы уравнений (1) называется базисное допустимое(х>0) решение.

1. из ур-й 1 и 4 вычтем ур-е 2.

2. 

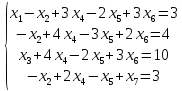
2 ур-е умножили на -1. Нужно добиться того, чтобы 2е ур-е стало разрешенным относительно какой-либо неизвестной

Утверждение: если система лин. уравнений содержит уравнение 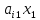++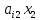…+= 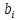(*), ≤0, j=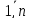, , то эта система не имеет неотрицательных(допустимых) решений.

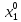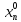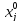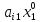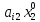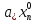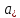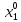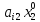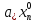Док-во. Существует Х=(,,…,), ≥0, j=. Подставим вместо неизвестных в (*) координаты Х. ++…+=-но это равенство невозможно, т.к. , ,…,<0, а ,,…,≥0 и ++…+≤0, а . Следовательно, получили противоречие,и следовательно теорема верная.

Замечание: если система лин. Уравнений содержит уравнения вида (*), т.е. все коэффициенты при неизвестных неположительны, а свободный член положительный, то такая система является несовместной к ОДР задач линейного программирования.

(3)

Теорема: пусть =min, 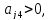тогда если в системе (2) выполнить однократные замещения с разрешающим элементом 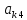, то все свободнве члены уравнений системы останутся неотрицательными.

Док-во: возьмем любой >0 и докажем что он останется неотрицательным

-------- =

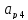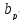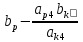
¦ ¦ 1 ситуация: 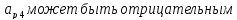, тогда

¦ ¦ 2 cитуация: 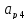≥0, тогда

-------

Чтобы найти исх оп решение сис лин уравнений, надо привести систему к разрешенному виду. Если при этом все свободные члены уравненйи будут неотрицательными, то базисное решение будет опорным. Если среди свободных членов ур-й будут отрицательные, то следует выполнить преобразования 1 и 2. Пусть после выполнения этих преобразований все св члены стали неотрицательными, но i-уравнение перестало быть разрешенным. Далее возможны сл случаи:

1. Пусть 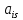>0, возьмем s-столбец за разрешающий и выберем разрешающий элемент согласно (3). Разр-й элемент оказался в i-строке. Выполним преобразования ж. гаусса, найдем базисные допустимые, т.е опорные решения.

2. Разр-й 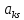, k≠i, св член 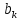>0. Выполним однократные замещения с разрешающим эл-м 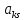. 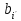=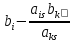→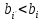, но i-уравнение останется неразрешенным. После конечного числа шагов придем к 1, либо в этом уравнении не останется положительным эл-в, тогда или система несовместна, или придем к 3.

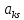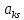3. , k≠i, но . Тогда в результате однократного замещения мы не уменьшим , поэтому прежде чем выполнять преобразования однократного замещения эле-та , нужно попробовать выбрать др разр-й столбец по другому получившемуся элементу в этой строке. Если этого сделать нельзя, то нужно выполнить преобразования однократного замещения. Тогда изменится состав базисных неизвестных и выбор разрешающего элемента надо начать сначала. И придем к 1 или 2 или установим несовместность