
билеты матан 3 мод 2010
.docx№1.Понятие первообразной. Неопр интеграл.
Функция F(x) на некотором промежутке X называется первообразной для функции f(x) на некотором множестве Х , если для любого x∈X выполняется условие F’(x)=f(x). ЛЕММА: функция, производная от которой на промежутке Х равна 0, постоянна на этом промежутке. Если F есть первообразная для f на Х, то любая другая первообразная может быть представлена в виде:
F(x)+c, где F(x) – первообразная, C – любая постоянная, F’(x)=f(x).
Если функция F(x) первообразная для функции f(x) на промежутке X, то множество функций F(x)+C, где C -- произвольная постоянная, называется неопределенным интегралом для функции f(x) на промежутке X и обозначается: ∫f(x)dx=F(x)+C
Операция восстановлении функции по ее производной называется интегрированием.
№2.Свойства неопределенного интеграла
1)производная от неопр интеграла равна подынтегральной функции 2)диффер. от неопределенного интеграла равен подынтегральному выражению 3) неопр интеграл от дифференциала некоторой функции равен сумме этой функции и произв. постоянной 4) Отличный от нуля постоянный множитель k можно выносить за знак неопределенного интеграла 5)неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов этих функций
№3 Таблица интегралов.

№4 Методы интегрирования.Метод разложения
Методы интегрирования:
-
Разложение
-
Непосредственное интегрирование
-
Замены переменной( подстановки)
-
По частям
Метод
разложения
Этот метод применяется
для интегрирования функций f(x),
представляющих собой алгебраическую
сумму нескольких
функций f1(x);
f2(x);...;
fn(x),
первообразные которых заранее известны
или
могут быть легко получены.
Тогда в соответствии со свойством 3
неопределенного интеграла получаем
![]()
№5 Метод замены переменной(подстановки)
Если
функция f
(
z
) определена и имеет первообразную при
z
![]() Z
,
а функция z
= g
( x
) имеет непрерывную производную при x
Z
,
а функция z
= g
( x
) имеет непрерывную производную при x
![]() X
и
её область значений g
( X
)
X
и
её область значений g
( X
)
![]() Z
,
то функция F
( x
) = f
[
g
( x
)] g'
( x
) имеет первообразную на Х
и
Z
,
то функция F
( x
) = f
[
g
( x
)] g'
( x
) имеет первообразную на Х
и
![]() F
( x
) dx
=
F
( x
) dx
=
![]() f
[ g
( x
)] • g'
( x
) dx
=
f
[ g
( x
)] • g'
( x
) dx
=
![]() f
( z
) dz
, где g(x)=z,
g´(x)dx=dz
f
( z
) dz
, где g(x)=z,
g´(x)dx=dz
№6. Метод интегрирования по частям.
# Пусть функции u(x) и v(x) определены и дифференцированы на некотором множестве х, и пусть функция u’(x)*v’(x) имеет на этом множестве первообразную, тогда на множестве х функция u(x)*v’(x) тоже имеет первообразную, причем справедлива следующая формула:
Su(x)*v’(x)dx=u(x)*v(x)-Su’(x)*v(x)dx
[u(x)*v(x)]’=u’(x)*v(x)+u(x)*v’(x)
u(x)*v’(x)=[u(x)*v(x)]’-u’(x)*v(x) dx
Su(x)*v’(x)dx=S[u(x)*v(x)]’dx-Su’(x)*v(x)dx
↓
=d(u(x)*v(x))=u(x)*v(x)
# метод интегрирования по частям в тригонометрической функции применяется дважды, в качестве u оба раза следует выбирать либо показат. функцию, либо тригонометр.
№7. Интегр-ие тригоном-их ф-ий. 1) Преобразование произв-ия в сумму. cosαx cosβx, sinαx sinβx, sinαx cosβx.
cosαx ∙ cosβx = ½(cos(α−β)x + cos(α+β)x)
sinαx∙ sinβx=½(cos(α−β)x – cos(α+β)x)
sinαx∙ cosβx=½(sin(α−β)x + sin(α+β)x)
![]()
![]()
![]()

№8. Интегрирование рациональных дробей
Выражение
![]() ,
где Pm(x)
и Qn(x)
– многочлены m-й
и n-й
степени, называется рациональной
дробью. Рациональная дробь называется
правильной, если m<n,
и неправильной, если m≥n.
Если дробь неправильная, следует
разделить числитель на знаменатель с
выделением частного и остатка.
,
где Pm(x)
и Qn(x)
– многочлены m-й
и n-й
степени, называется рациональной
дробью. Рациональная дробь называется
правильной, если m<n,
и неправильной, если m≥n.
Если дробь неправильная, следует
разделить числитель на знаменатель с
выделением частного и остатка.
Теорема: любая правильная элементарная дробь может быть представлена в следующем виде: (Pm(x)/Qn(x) ) = = A1/(x-a)+A2/(x-a)2+...+Ak/(x-a)k+(B1x+C1)/(x2+px+q)+(B2x+C2)/(x2+px+q)2+...+ (Bex+Ce)/(x2+px+q)e
Это разложение называется разложением дробно-рац ф-и на элементарные дроби Qn(x)=(x-a)k
Если при разложении скобка повторяется к раз, то к-корень кратности. Правую часть мы приводим к общему знаменателю, дальше сравниваем числители дробей, т.к там присутствуют многочлены, то приравниваем коэффициенты при одинаковых степенях Х, получаем систему для нахождения неизвестных коэффициентов.
Имеется 4 типа правильных дробей:





№10. Свойства определенного интеграла.
1)![]() 2)
2)![]()
3)
![]()
4)
![]()
5)
![]()
№11. Оценки определенных интегралов
-
Если на отрезке [a;b] f(x)≥0, то : ∫f(x)dx≥0
-
[a;b] ; f(x)≤g(x) => ∫ba f(x)dx≤ ∫ba g(x)dx
h(x)=g(x)-f(x)≥0
0≤ ∫ba h(x)dx
-
[a;b] ; f(x), то |∫ba f(x)dx |≤ ∫ba |f(x)| dx
Доказательство: -|f(x)|≤f(x)≤|f(x)|
-∫ba |f(x)| dx ≤ ∫ba f(x)dx ≤ ∫ba |f(x)| dx
|a|≤b -b≤a≤b
Если на отрезке [a;b] имеет место неравенство |f(x)| ≤ k , то |∫ba f(x) dx |≤ k (b-a)
-
Если функция достигает своих минимальных (m) и максимальных (М) значений на [a;b], то имеет место следующая оценка m|b-a| ≤ ∫f(x)dx ≤ M|b-a|
№9. Определенный интегралл его геометрический смысл.
Если существует конечный предел суммы δ=f(η1)*∆x1+f(η2)*∆x2+...+f(ηn)*∆xn при x→0, то этот предел называется определенным интегралом f(x) на [a;b], где a, b - верхний и нижний пределы интегрирования.
∫baf(x)dx= lim(λ→0) ∑ni=1f(ηi)*∆xi
Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Для этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х0<x1<...<xn) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
Умножим значением функции ƒ(ci) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений
![]()
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:
![]()
С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max∆xi →0:
![]()
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
В этом состоит геометрический смысл определенного интеграла.
№12.Теорема о среднем.
Если
f(x)
непрерывна на отрезке [a,b],
то существует точка
![]() ,
такая что
,
такая что
![]() .
.
![]() Док-во.
Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
m
и наибольшее M
значения. Тогда
Док-во.
Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
m
и наибольшее M
значения. Тогда
![]() .
Число
.
Число
![]() заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m
и M.
Таким образом, существует точка
заключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m
и M.
Таким образом, существует точка
![]() ,
такая что
,
такая что
![]() .
.
№13 Определенный интеграл с переменным верхним пределом
верхний
предел интеграла может меняться, т.е.
что x
- переменная, в результате интеграл
будет функцией Ф(x)
своего верхнего предела:
![]() .
Легко доказать, что если f(t)
интегрируема, то Ф(x)
непрерывна, но для нас важнее следующая
фундаментальная теорема:
.
Легко доказать, что если f(t)
интегрируема, то Ф(x)
непрерывна, но для нас важнее следующая
фундаментальная теорема:
![]() Теорема
об интеграле с переменным верхним
пределом.
Если функция f(t)
непрерывна в окрестности точки t
= x,
то в этой точке функция Ф(x)
дифференцируема, и
Теорема
об интеграле с переменным верхним
пределом.
Если функция f(t)
непрерывна в окрестности точки t
= x,
то в этой точке функция Ф(x)
дифференцируема, и
![]() .
.
![]() Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом пределе.
Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом пределе.
![]() Док-во.
Дадим верхнему пределу x
приращение
Док-во.
Дадим верхнему пределу x
приращение
![]() .
Тогда
.
Тогда
![]()
![]()
![]() ,
где c
- точка, лежащая между x
и
,
где c
- точка, лежащая между x
и
![]() (существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).
(существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).
![]() .
Устремим
.
Устремим
![]() .
При этом
.
При этом
![]() (c-
точка, расположенная между x
и
(c-
точка, расположенная между x
и
![]() ).
Так как f(t)
непрерывна в точке t
= x,
то
).
Так как f(t)
непрерывна в точке t
= x,
то
![]() .
Следовательно, существует
.
Следовательно, существует
![]() ,
и
,
и
![]() .
Теорема доказана.
.
Теорема доказана.
Следствия:
1.Любая непрерывная функция f(x)
имеет первообразную, и эта первообразная
определяется формулой
![]() ,
2. формула Ньютона-Лейбница, или основная
формула интегрального исчисления.
,
2. формула Ньютона-Лейбница, или основная
формула интегрального исчисления.
№ 14. Формула Ньютона-Лейбница
Если
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и
F —
ее первообразная на этом отрезке, то
имеет место равенство
и
F —
ее первообразная на этом отрезке, то
имеет место равенство

Док-во:
в силу того, что f(x)
непрерывна на [a;b]
, она имеет первообразную F
(x)
во всех точках промежутка. Существует
С*, такое, что
 = F(x)
+ C*.
Равенство верно при любом х из [a;b].
= F(x)
+ C*.
Равенство верно при любом х из [a;b].
X=a,
 ,
F(a)+C*=0, C*=-F(a)
,
F(a)+C*=0, C*=-F(a)
X=b,
 *=
F(b)-F(a), чтд.
*=
F(b)-F(a), чтд.
№15 Особенности вычисления определенных интегралов.
Пусть функция у = f(x) определена во всех точках отрезка [а; b]. Произвольной конечной системой точек x1, i = 0, 1, ... , п, таких что
а = х0 < х1 < х2 < ... < хn-1 < хn = b
разбиваем
отрезок [а; b] на отрезки [xi;
xi+1];
i = 0, 1, ... , n - 1.
На каждом из полученных
отрезков произвольным образом выбираем
точку ci+1:
ci+1
![]() [xi;
xi+1],
и рассчитываем значение функции у =
f(x) в этих точках.
Составляем так
называемую интегральную сумму,
соответствующую данной разбивке xi
и выбору точек ci+1,
i = 0, 1, ... , n - 1 :
[xi;
xi+1],
и рассчитываем значение функции у =
f(x) в этих точках.
Составляем так
называемую интегральную сумму,
соответствующую данной разбивке xi
и выбору точек ci+1,
i = 0, 1, ... , n - 1 :
![]() где
где
![]() xi
= хi+1
- хi
Обозначим
через
xi
= хi+1
- хi
Обозначим
через
![]() =
max |
=
max |![]() xi|,
т. е.
xi|,
т. е.
![]() -
длина наибольшего из отрезков [xi;
xi+1].
Определение
1. Если при
-
длина наибольшего из отрезков [xi;
xi+1].
Определение
1. Если при
![]() ->
0 (n ->
->
0 (n ->
![]() )
существует конечный предел интегральных
сумм
)
существует конечный предел интегральных
сумм
![]() ,
то этот предел называется определенным
интегралом функции у = f(x) на отрезке
[а; b]:
,
то этот предел называется определенным
интегралом функции у = f(x) на отрезке
[а; b]:
![]() Определение
2. Если существует определенный интеграл
функции у = f(x) на некотором отрезке, то
функция называется интегрируемой на
этом отрезке.
К числу наиболее важных
типов интегрируемых функций относятся
непрерывные функции; ограниченные
функции, имеющие конечное число точек
разрыва; ограниченные монотонные
функции.
Определение
2. Если существует определенный интеграл
функции у = f(x) на некотором отрезке, то
функция называется интегрируемой на
этом отрезке.
К числу наиболее важных
типов интегрируемых функций относятся
непрерывные функции; ограниченные
функции, имеющие конечное число точек
разрыва; ограниченные монотонные
функции.
№16. Вычисление площади плоской фигуры.
Для вычисления площади плоской фигуры используют следующие этапы:
1) определяется вид искомой площади фигуры
2)устанавливаются пределы интегрирования
3)устанавливаются участки, на которых подынтегральная функция положительная и отрицательная
4)берутся интегралы, на каждом участке находится суммарная абсолютная величина площадей этих участков
Если требуется вычислить S фигуры, ограниченной двумя кривыми на участке
[a,b] y1= f1(x), y2=f2(x), то искомая S находится как разность площадей криволинейных трапеций, ограниченных разными кривыми
S= a∫b f1(x)dx - a∫b f2(x)dx = a∫b (f1(x) - f2(x))dx
В некоторых случаях пределы интегрирования не заданы, и они находятся в процессе решения.
№17. Вычисление площади поверхности тела вращения
Найдем
площадь поверхности, которая образуется
вращением кривой
![]() вокруг
оси
вокруг
оси
![]() ,
где
,
где
![]() .
.
Указанную площадь можно получить вычислением определенного интеграла:
![]()
Теперь
рассмотрим случай, когда вращаем кривую
![]() вокруг
оси
вокруг
оси
![]() ,
где
,
где
![]()
В этом случае площадь определяется вычислением следующего определенного интеграла:
![]()
№18. Вычисление объема тела вращения.
Рассмотрим
тело, которое образовано вращением
вокруг оси Ox
криволинейной трапеции, ограниченной
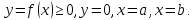
Объем этого тела
 .
.
Если криволинейная, ограниченная
 ,
вращается вокруг оси Oy,
то объем полученного тела вычисляется
по формуле
,
вращается вокруг оси Oy,
то объем полученного тела вычисляется
по формуле
 .
.
Докажем
сформулированные утверждения. Заметим,
что если
 - разбиение отрезка
- разбиение отрезка
 ,
то
,
то
 будет представлять приближенно объем
тела вращения. Это выражение можно
рассматривать как интегральную сумму.
Переходя к пределу, получаем
будет представлять приближенно объем
тела вращения. Это выражение можно
рассматривать как интегральную сумму.
Переходя к пределу, получаем
 .
.
№19. Вычисление длины дуги кривой.
Пусть
известна функция
![]() и
требуется найти длину дуги, заданной
функцией
и
требуется найти длину дуги, заданной
функцией
![]() ,
где
,
где
![]() .
.
Для
определения длины дуги
![]() необходимо
вычислить определенный
интеграл:
необходимо
вычислить определенный
интеграл:
![]()
№20. Несобственные интегралы.
Будем
считать, что
 определена и непрерывна в
определена и непрерывна в
 и стремится к бесконечности при
и стремится к бесконечности при
 .
Составим интеграл
.
Составим интеграл
 .
.
Очевидно,
что в этом случае интеграл зависит от
значений ε. Перейдем к пределу при
 и назовем этот предел несобственным
интегралом первого рода:
и назовем этот предел несобственным
интегралом первого рода:
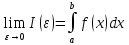 .
.
Если
 сущ-ет
и конечен, то несобственный интеграл
наз. сходящимся. Если этот предел не
сущ-ет или бесконечен, то несобственный
интеграл наз. расходящимся.
сущ-ет
и конечен, то несобственный интеграл
наз. сходящимся. Если этот предел не
сущ-ет или бесконечен, то несобственный
интеграл наз. расходящимся.
Предположим,
что
 непрерывна в любом конечном промежутке
непрерывна в любом конечном промежутке
 ,
тогда сущ-ет определенный интеграл
,
тогда сущ-ет определенный интеграл
 .
В данном случае величина b
задает верхний переменный предел
интегрирования.
.
В данном случае величина b
задает верхний переменный предел
интегрирования.
Устремим b к бесконечности и рассмотрим предел
 ,
,
который назовем несобственным интегралом второго рода. Если этот предел сущ-ет и конечен, то интеграл наз. сходящимся. Если предел не сущ-ет или бесконечен, то несобственный интеграл наз. расходящимся.
Следует отметить важное св-во несобственных интегралов.
Известно, что для опред. интеграла справедливо утверждение:
если
сущ-ет
 ,
то сущ-ет и интеграл
,
то сущ-ет и интеграл
 .
.
В
случае несобственных интегралов
получаем след. утверждение: из сходимости
несобственного интеграла от
 следует сходимость несобственного
интеграла от
следует сходимость несобственного
интеграла от
 .
Примем это утверждение без док-ва.
.
Примем это утверждение без док-ва.
Если
несобственный интеграл
 сходится, то говорят, что интеграл
сходится, то говорят, что интеграл
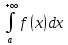 сходится абсолютно. (Аналогично
абсолютная сходимость опред-ся для
несобственного интеграла первого
рода).
сходится абсолютно. (Аналогично
абсолютная сходимость опред-ся для
несобственного интеграла первого
рода).
Следует
заметить, что сходимость несобственного
интеграла
 не влечет сходимости несобственного
интеграла
не влечет сходимости несобственного
интеграла
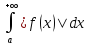 .
Такую сходимость будем наз. условной.
.
Такую сходимость будем наз. условной.
№21.Теоремы сравнения
Т
1. Если
φ(х),
f(x)–
неотрицательные функции
и φ(х)
функции
и φ(х) f(x)
для
f(x)
для
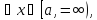 то:
то:
-
Из сходимости
 следует сходимость
следует сходимость
 ;
; -
Из сходимости
 следует расходимость
следует расходимость

Т
2. Если
φ(х),
f(x)–
неотрицательные функции
и существут конечный предел
функции
и существут конечный предел
 ,
то несобственные интегралы
,
то несобственные интегралы
 и
и
 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
№23. Обыкновенные диф уравнения. Их решения.
Обыкновенным диф.уравнением называется соотношение вида F(x,y,y’,y’’,…y(n))=0 (1), которая связывает первый независимый аргумент (х), неизвестную функцию (у) и ее производную.
Порядок старшей производной в диф.уравнении называется порядком диф.уравнения.
Замечание: y(i) не обязательно входит в уравнение (1)
Решением диф.уравнения называется функция y=φ(x), которая при подстановке ее в (1) превращает последнее в тождество.
График решения диф.уравнения – интегральная кривая этого уравнения.
К основным задачам теории диф.уравнений относятся: 1) разыскание всех решений; 2) изучение свойств этих решений.
Решить диф. уравнение=проинтегрировать.
Общим решением диф.уравнения (1) называется такая функция y=ф(x, y, C1,…,Cn)(2), где n- порядок диф.уравнения.
Если каждой из const Ci присвоить определенное значение, то решение, полученное после подстановки этих значений в (2) будет называться частным.
Диф.уравнение называется линейным, если все производные функции и сама ф-я входит в уравнение (1) в первой степени.
a0(x)*y(n)+a1(x)*y(n-1)+…+a(n-1)(x)*y’+an(x)*y=f(x)
№22. Применение интегралов в экономике
Пусть
функция z=f(x)
описывает изменение производительности
некоторого производства с течением
времени. Тогда объем продукции
![]() ,
произведенной за промежуток времени
,
произведенной за промежуток времени
![]() вычисляется по следующей формуле:
вычисляется по следующей формуле:
![]()
Возможность учета влияния различных факторов на изменение производительности производства связана с использованием,например, так называемых функций Кобба-Дугласа. Вэтом случае производительность f(t) представляется в виде произведения трех сомножителей:
![]()
Доход
от реализации количества товара x0
по равновесной цене р0 равен проиведению
х0р0. Если предполагать непрерывное
снижение цены рD=f(0)
до равновесной р0 по мере удовлетворения
спроса,то доход составит![]() . Величина денежных средств
. Величина денежных средств
![]() сберегается потребителями, если
предполагать продажу товара по
равновесной цене р0, поэтому С называется
также выигрышем потребителей.
сберегается потребителями, если
предполагать продажу товара по
равновесной цене р0, поэтому С называется
также выигрышем потребителей.
Аналогично,
![]() называется
выигрышем потребителей.
называется
выигрышем потребителей.
