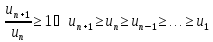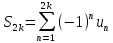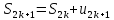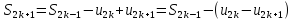билеты матан 3 мод 2010
.docx
№24. Дифференциальные уравнения с разделяющимися переменными.
Диф.уравнения вида Ф(y)dy=f(x)dx называется диф.ур-м с разделенными переменными.
Диф. ур-ие вида Фı(у)fı(х)dy=Ф2(у)f2(х)dx наз. диф. ур-ем с разделяющимися перем-ми.
S(Ф1(у)/Ф2(у))dy=S(f2(x)/f1(x))dx
Замечание: деление при разделении переменных может привести к потере корней, поэтому нужно проверить, не является ли решением полученное диф.ур-е.
f1(x)*Ф2(y)
f1(x)=0 и Ф2(у)=0
Замечание: Если правая часть уравнения y’=f(x,y) имеет вид f(ax+by+c), где a,b,c – const, может с помощью замены ax+by+c=z быть приведенным к диф.ур-ю с разделяющ. перемен-ми и приводящими к ним.
№25. Однородные дифференциальные уравнения.
Ф-я f(x, y) называется однородной ф-ей своих аргументов измерения n, если справедливо следующее тождество: f(xn; yn)’=tnf(x,y)
f(x,y)=x2-2xy+3y2
f(tx;ty)=(tx)2-2(tx)*(ty)+3(ty)2=t2x2-2t2xy+3t2y2=t2(x2-2xy+3y2)=t2f(x,y)
при n=0, мы имеем ф-ю нулевого измерения
Диф.ур-е y’=f(x,y) называется однородным относительно х и у, если правая часть (f(x,y)) – есть однородная функция нулевого измерения.
№26. Линейные дифф. уравнения первого порядка.
Линейным дифф. уравнением первого порядка наз. линейное уравнение относительно неизвестной функции и ее производной, вида
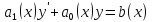 или
или
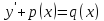 y’+p(x)y = q(x)
y’+p(x)y = q(x)
Предположим
сначала, что правая часть равна нулю.
Тогда
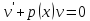 явл. уравнением с разделяющимися
переменными:
явл. уравнением с разделяющимися
переменными:

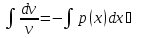
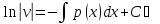
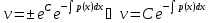
Замечание. Под неопред. интегралом часто будем понимать только одну первообразную.
Для
решения исходного уравнения
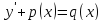 применяется метод вариации произвольных
постоянных. Предположим, что С в
применяется метод вариации произвольных
постоянных. Предположим, что С в
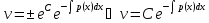 есть некотор. функция от x,
и решение будем искать в виде
есть некотор. функция от x,
и решение будем искать в виде
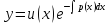 .
.
Подставив
это выражение в
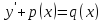 ,
найдем
,
найдем
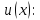
 .
.
Отсюда общ. решение
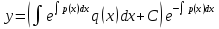 .
.
№27. Уравнения в полных дифференциалах.
Диф.ур-ми вида M(x,y)dx+N(x,y)dy=0 (*) называется ур-м в полных диф-х, если его левая часть является диф-м некоторой ф-и u(x,y)
M(x,y)dx+N(x,y)dy=du=u’xdx+u’ydy
Для того, чтобы ур-е (*) являлось ур-м в полн диф-х необходимо и достаточно, чтобы выполнялось следующее условие: ðM/ðy=ðN/ðx
u(x,y)=SM(x,y)dx+Ф(y)
u(x,y)=SN(x,y)dy+f(x)
№28.Диф уравнения 2 порядка
Общий вид дифференциального уравнения второго порядка:
|
F(x,y,y´ ,y´´)=0 |
(2) |
если это уравнение разрешено относительно старшей производной, то
|
y´´=¦ (x,y,y´ ). |
(3) |
Общее решение дифференциального уравнения второго порядка имеет вид:
|
y=j (x,C1,C2), |
(4) |
где C1 и C2 - две независимые произвольные постоянные. Геометрически общее решение (4) представляет собой бесконечную совокупность интегральных кривых, зависящую от двух независимых
параметров C1 и C2, проходящих через точку M(x,y). Вообще говоря, через выбранную точку M0(x0,y0) проходит пучок интегральных кривых.
Поэтому, чтобы из семейства интегральных кривых выделить конкретную интегральную кривую Г, недостаточно указать точку M0(x0,y0), через которую должна проходить выбранная кривая Г, а следует указать ещё и направление в котором кривая Г проходит через точку M0(x0,y0). Таким образом мы пришли к начальным условиям (н.у.) и из этой системы можно определить C1 и C2, тем самым - найти частное решение y=j (x), удовлетворяющее исходному ДУ-II и заданным начальным условиям.
№29.Интегрируемые
типы дифференциальных уравнений второго
порядка.
1)уравнения,не
содержащие явно функцию у
Рассмотрим
уравнение
y´´=f(x,y’)
положим,что
y´=z(x),y’’=z’(x).Тогда получим уравнение
1ого порядка относительно ф-ции z(x):
z’=f(x,z).Проинтегрируем его в общем виде:
z=φ(x,C1),и
вернемся к исходным переменным :
y’=φ(x,C1).Отсюда
получим общее решение исходного
уравнения y=∫φ(x,C1)dx
+ C2
2)уравнения,не
содержащие явно х
Рассмотрим ур-е :
y’’=f(y,y’).Сделав замену dy/dx=p(y),
(d2x/dx2)=(dp/dy)*(dy/dx)=p’p,получим
p’=(1/p)*f(y,p).Пусть общее решение этого
уравнения имеет вид p=g(y,C1).тогда
y’=g(y,C1)
и общий интеграл имеет вид ∫dy/g(y,C1)=x+C2.
№30.Линейные
дифференциальные уравнения второго
порядка с постоянными коэффициентами.
Линейное
дифференциальное уравнение с постоянными
коэффициентами - обыкновенное
дифференциальное уравнение вида:
![]() где
y
= y(t) искомая функция,
y(k) = y^(k)(t)
- её k-тая производная,
где
y
= y(t) искомая функция,
y(k) = y^(k)(t)
- её k-тая производная,
![]() -
фиксированные числа,
f(t)- заданная
функция (когда f(t)=0, имеем линейное
однородное уравнение, иначе линейное
неоднородное уравнение).
№31.Применение
дифференциальных уравнений в экономике.
-
фиксированные числа,
f(t)- заданная
функция (когда f(t)=0, имеем линейное
однородное уравнение, иначе линейное
неоднородное уравнение).
№31.Применение
дифференциальных уравнений в экономике.
примеры: непрерывная динамическая модель Кейнса, модель роста Харрода-Домара, уравнение Ферхюльста (логистическое уравнеие),модель Солоу, модель Гудвина, модель хищник-жертва и т.д.
Моделирование скорости роста численности населения: 1. Скорость роста численности населения пропорциональна самой численности y’(t)=k*y(t), 2. Миграция присутствует y’(t)=ky(t)+q(t)
Моделирование процесса распространения информации: y’(t)=λy(t)*(N-y(t)), где N – потенциальное число покупателей нового товара, y(t)- число покупателей, знающих о товаре в момент t.
№32. Числовые ряды. Сходимость числового ряда.
Рассмотрим
последовательность
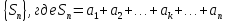 =
=
 -
частичные
суммы. Если число слагаемых устремит
к бесконечности, то получим бесконечную
сумму
-
частичные
суммы. Если число слагаемых устремит
к бесконечности, то получим бесконечную
сумму
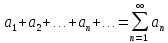 .
.
Назовем
эту сумму числовым рядом, а
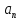 – членами ряда.
– членами ряда.
Если
сущ-ет конечный предел последовательности
частичных сумм
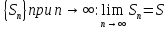 ,
то говорят, что ряд
,
то говорят, что ряд
 сходится, а число S
наз. суммой ряда. Именно этот смысл
имеет запись
сходится, а число S
наз. суммой ряда. Именно этот смысл
имеет запись
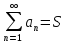 .
.
Если
последовательность
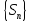 не имеет конечного предела, то говорят,
что ряд
не имеет конечного предела, то говорят,
что ряд
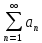 расходится.
расходится.
Пусть
ряд
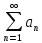 сходится к сумме S.
Рассмотрим разность между величиной
сходится к сумме S.
Рассмотрим разность между величиной
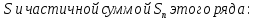
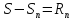 .
Величина
.
Величина
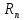 наз. остатком ряда. Очевидно, что
наз. остатком ряда. Очевидно, что
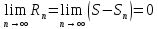 .
.
№33. Свойства сходящихся рядов.
-
Если ряд сходится, тогда последовательность членов ряда { an } имеет предел равный нулю. (Свойство следует из Критерия Коши для сходимости последовательности { Sn }. )
-
(Сходимость линейной комбинации) Если два ряда сходятся, то сходится и их линейная комбинация, причем :
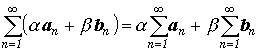 (Свойство
следует из свойства сходимости линейной
комбинации последовательностей,
примененного к последовательностям
частичных сумм.)
(Свойство
следует из свойства сходимости линейной
комбинации последовательностей,
примененного к последовательностям
частичных сумм.)
-
Для ряда
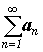 назовем
k-ым
остатком ряда ряд вида
назовем
k-ым
остатком ряда ряд вида
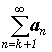 .
Если ряд сходится, тогда сходится и
любой его остаток. Если сходится
какой-то из остатков, тогда сходится
и весь ряд, причем если обозначить Rn
сумму n-го
остатка ряда, тогда при любых значениях
n
выполнено равенство : S
= Sn
+ Rn
.
Если ряд сходится, тогда сходится и
любой его остаток. Если сходится
какой-то из остатков, тогда сходится
и весь ряд, причем если обозначить Rn
сумму n-го
остатка ряда, тогда при любых значениях
n
выполнено равенство : S
= Sn
+ Rn -
Из предыдущего свойства следует, что остатки сходящегося ряда стремятся к нулю.
№34. Необходимый признак сходимости рядов: Пусть числовой ряд
|
u1+u2+...+un+… |
|
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю Доказательство. Из условия теоремы имеем
![]()
![]()
Так как Sn - Sn-1 = un, то
![]()
Следует
отметить, что этот признак является
лишь необходимым, но не достаточным
признаком сходимости ряда, так как
можно указать ряд, для которого
выполняется равенство
![]() ,
,
а
он, однако не является сходящимся.
Так
гармонический ряд
![]() ,
,
для
которого
![]() ,расходится.
,расходится.
№35.
Необходимое и достаточное условие
сходимости ряда Для
того, чтобы ряд
![]() был
сходящимся необходимо и достаточно,
чтобы для любого
был
сходящимся необходимо и достаточно,
чтобы для любого
![]() существовал
номер N
такой, что при n>N
и любом p>0
выполнялось бы неравенство
существовал
номер N
такой, что при n>N
и любом p>0
выполнялось бы неравенство
![]() .
Доказательство:
.
Доказательство:
№36.
Интегральный признак сходимости ряда
Пусть
![]() - непрерывная, неотрицательная, монотонно
убывающая функция, определенная при
- непрерывная, неотрицательная, монотонно
убывающая функция, определенная при
![]() .
Тогда ряд
.
Тогда ряд
![]() и
интеграл
и
интеграл
![]() либо оба сходятся, либо оба расходятся.
Доказательство.
Ввиду монотонности при всех
либо оба сходятся, либо оба расходятся.
Доказательство.
Ввиду монотонности при всех
![]() выполняются
неравенства
выполняются
неравенства
![]() .
Интегрируя, получаем
.
Интегрируя, получаем
![]() .
Тогда
.
Тогда
![]() ,
или
,
или
![]() .
Поэтому если
.
Поэтому если
![]() сходится,
то
сходится,
то
![]() .
Тогда
.
Тогда
![]()
![]() и
и
![]() ,
,
![]() ряд сходится. Пусть теперь наоборот,
известно, что ряд сходится. Тогда
ряд сходится. Пусть теперь наоборот,
известно, что ряд сходится. Тогда
![]() .
Взяв произвольное
.
Взяв произвольное
![]() выберем
выберем
![]() так,
чтобы
так,
чтобы
![]() .
Тогда
.
Тогда
![]() .
Значит,
.
Значит,
![]() сходится.
сходится.
№37. Признак сравнения
Если
![]() то
из сходимости ряда
то
из сходимости ряда
![]() следует
сходимость ряда
следует
сходимость ряда
![]() ,
а из расходимости ряда
,
а из расходимости ряда
![]() -
расходимость ряда
-
расходимость ряда
![]() Предельный
признак сравнения
Предельный
признак сравнения
Если
![]() то
при
то
при
![]() ряды
ряды
![]() и
и
![]() или
оба сходятся, или оба расходятся; при
l
= 0
из сходимости ряда
или
оба сходятся, или оба расходятся; при
l
= 0
из сходимости ряда
![]() следует
сходимость ряда
следует
сходимость ряда
![]() ;
при
;
при
![]() из
расходимости ряда
из
расходимости ряда
![]() следует
расходимость ряда
следует
расходимость ряда
![]() .
В частности, если
.
В частности, если
![]() при
при
![]() то
ряды
то
ряды
![]() и
и
![]() или
оба сходятся, или оба расходятся.
или
оба сходятся, или оба расходятся.
38.Признак Даламбера
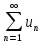 (1)
(1)
1)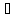 q,
если сущ-ет такое число qϵ(0;1)
и такой номер
q,
если сущ-ет такое число qϵ(0;1)
и такой номер
 ,
что имеет место следующее нерав-во:
,
что имеет место следующее нерав-во:
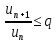
для
всех
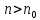 ,
в этом случае ряд (1) сходится.
,
в этом случае ряд (1) сходится.
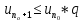
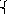
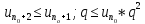

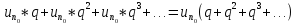
2)
 если сущ-ет такой номер
если сущ-ет такой номер
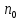 ,
что имеет семто следующее нерав-во
,
что имеет семто следующее нерав-во
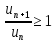 ,
то ряд (1) не сходится
,
то ряд (1) не сходится

Значит эта числовая последовательность ограничена снизу. Не выполняется признак сходимости ряда.
Пусть
существует предел
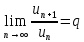 ,
тогда
,
тогда
если
q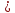 1,
то ряд (1) сходится
1,
то ряд (1) сходится
-
если q
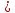 1,
то ряд (1) расходится
1,
то ряд (1) расходится -
если q=1, требуются дополнительные исследования
39.Признак Каши
Пусть
задан ряд
 (1) с положительными членами, тогда:
(1) с положительными членами, тогда:
-
Если
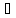 q
q и некоторый номер
и некоторый номер
 такое, что
такое, что
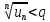 ;
;
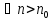 ,
то ряд (1) сходится.
,
то ряд (1) сходится. -
Если
 такое, что
такое, что
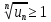 ;
;
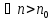 ,
то ряд (1) расходится.
,
то ряд (1) расходится.
Док-во:
-
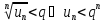 (ряд
– бесконечно убывающая геометр.
прогрессия) который сходится
(ряд
– бесконечно убывающая геометр.
прогрессия) который сходится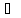 по признаку сравнения сходится ряд
(1).
по признаку сравнения сходится ряд
(1). -
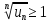
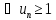 ,
т.к. не выполняется необходимое условие
сходимости ряда, ряд расходится.
,
т.к. не выполняется необходимое условие
сходимости ряда, ряд расходится.
40. Знакопеременные ряды. Признак Лейбница.
Опр. Ряд называется знакопеременным, если он содержит ∞ множество как положительных членов, так и отрицательных.
Опр.
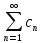 (2) Числовой ряд (2) называется
знакочередующимся, если члены ряда
(2) Числовой ряд (2) называется
знакочередующимся, если члены ряда
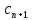 и
и
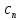 имеют разные знаки для
имеют разные знаки для
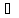 n
(любые 2 соседних числа имеют разные
знаки).
n
(любые 2 соседних числа имеют разные
знаки).
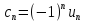 ;
;
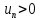
Признак Лейбница
Пусть
задан ряд
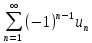 ,
тогда:
,
тогда:
-
если
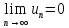 (предел n-ого
члена =0);
(предел n-ого
члена =0); -
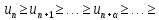 0
(ряд является монотонно убывающим)
0
(ряд является монотонно убывающим)
то этот ряд сходится.
Док-во.
Рассмотрим чётные частичные суммы

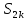 – монотонно
возрастает
– монотонно
возрастает
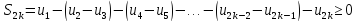
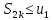
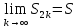
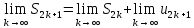
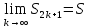
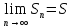
Замечание. Для ряда (2) справедливо следующее нерав-во

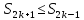
Последовательность частичных сумм убывает (ограничена снизу)
№41. Абсолютно сходящиеся ряды.
Ряд
![]() называют
абсолютно
сходящимся числовым рядом,
если сходится ряд
называют
абсолютно
сходящимся числовым рядом,
если сходится ряд
![]() .Свойства:
1)из сходимости ряда
.Свойства:
1)из сходимости ряда
![]() вытекает
сходимость ряда
вытекает
сходимость ряда
![]() .
2)При исследовании абсолютной сходимости
ряда используют признаки сходимости
рядов с неотрицательными членами.
3)Если ряд
.
2)При исследовании абсолютной сходимости
ряда используют признаки сходимости
рядов с неотрицательными членами.
3)Если ряд
![]() расходится,
то для выявления условной сходимости
числового ряда используют более тонкие
признаки: Признак Лейбница, признак
Абеля, признак Дирихле.
расходится,
то для выявления условной сходимости
числового ряда используют более тонкие
признаки: Признак Лейбница, признак
Абеля, признак Дирихле.
№42. Степенные ряды. Теорема Абеля об интервале сходимости степенного ряда.
О: Степенным рядом (ср.) называется ф.р. вида
![]()
При![]() =
0 получаем ряд по степеням х.
=
0 получаем ряд по степеням х.
![]() (30.2)
(30.2)
Для того чтобы найти область сходимости ср., докажем теорему Абеля.
Т.
(Абеля): Если степенной ряд (30.2) сходится
при![]() то
он абсолютно сходится
то
он абсолютно сходится![]() Если
ряд (30.2) расходится в т.
Если
ряд (30.2) расходится в т.![]() то
он расходится
то
он расходится![]()
Пусть
ряд![]() сходится,
тогда
сходится,
тогда![]() Поскольку
функция, имеющая предел, ограничена,
то
Поскольку
функция, имеющая предел, ограничена,
то![]() Перепишем ряд (30.2) в виде
Перепишем ряд (30.2) в виде
![]() Для
ряда из абсолютных величин его членов
Для
ряда из абсолютных величин его членов
![]() 30.3)
30.3)
имеем![]() >
причем геометрическая прогрессия
>
причем геометрическая прогрессия
![]() сходится
при
сходится
при![]() Таким
образом, при
Таким
образом, при![]() по
первому признаку сравнения ряд (30.3)
сходится, тогда по признаку абсолютной
сходимости ряд (30.2) сходится абсолютно.
по
первому признаку сравнения ряд (30.3)
сходится, тогда по признаку абсолютной
сходимости ряд (30.2) сходится абсолютно.
Пусть
теперь ряд (30.2) расходится при![]() Предположим
в противоречие с утверждением теоремы,
что
Предположим
в противоречие с утверждением теоремы,
что![]() при
котором ряд (30.2) сходится. Но по доказанному
выше ряд (30.2) должен тогда сходиться в
т.
при
котором ряд (30.2) сходится. Но по доказанному
выше ряд (30.2) должен тогда сходиться в
т.![]() Полученное
противоречие с условием доказывает
теорему
Полученное
противоречие с условием доказывает
теорему
№43. Определение интервалов сходимости степенных рядов.
Из
теоремы Абеля следует, что если![]() —
точка сходимости ряда (30.2), то ряд
сходится абсолютно во всех точках
интервала
—
точка сходимости ряда (30.2), то ряд
сходится абсолютно во всех точках
интервала![]() Если
Если![]() —
точка расходимости (30.2), то ряд расходится
во всех точках интервалов
—
точка расходимости (30.2), то ряд расходится
во всех точках интервалов![]() Отсюда
делаем вывод, что существует такое
число R, что на (-R, R) ряд (30.2) сходится
абсолютно, а на
Отсюда
делаем вывод, что существует такое
число R, что на (-R, R) ряд (30.2) сходится
абсолютно, а на
![]() расходится.
Таким образом, справедлива следующая
теорема.
расходится.
Таким образом, справедлива следующая
теорема.
Т:
Областью сходимости ряда (30.2) является
интервал (-R, R), В каждой точке этого
интервала ряд сходится абсолютно, а на
интервалах![]() —
расходится
—
расходится
Интервал
(-R, R) называется интервалом сходимости
ряда (30.2), a R — его радиусом сходимости.
Для некоторых рядов интервал сходимости
вырождается в точку (R= 0), для других —
охватывает всю ось OX(R=![]()
![]()
Если![]() то
ряд из абсолютных величин членов (30.2)
сходится и ряд (30.2) сходится абсолютно.
Обозначим
то
ряд из абсолютных величин членов (30.2)
сходится и ряд (30.2) сходится абсолютно.
Обозначим
![]() (30.4)
(30.4)
При![]() ряд
(30.2) расходится, так как общий член ряда
ряд
(30.2) расходится, так как общий член ряда![]() не стремится к 0. Таким образом, формула
(30.4) дает радиус сходимости.
не стремится к 0. Таким образом, формула
(30.4) дает радиус сходимости.