18 Статистические оценки Точечные

Пусть выборка

Zn

Δ =

col(X1, ... , Xn)

соответствует функции распределения

F(x,θ)

Δ =

P{X ≤ x},

зависящей от неизвестного параметра θ. Точечной (выборочной) оценкой неизвестного параметра θ называется функция

^ θ(Zn)

случайной выборки Z_n, реализация

^ θ(zn)

которой принимается за приближенное значение θ.

2Оценка

^ θ(Zn)

параметра θ называется несмещенной, если ее МО при любом n равно θ, т.е.

M[	^ θ(Zn)] = θ.

3Оценка

^ θ(Zn)

называется состоятельной, если она сходится по вероятности к θ, т.е.

^ θ(Zn)

P →

θ при n → ∞.

Свойствами состоятельности и несмещенности могут обладать сразу несколько оценок неизвестного параметра θ.

Несмещенная оценка

^ θ

*(Zn)

параметра θ называется эффективной, если

D[

^ θ

*(Zn)] ≤ D[

^ θ

(Zn)]

для всех несмещенных оценок

^ θ(Zn),

т.е. ее дисперсия минимальна по сравнению с дисперсиями других несмещенных оценок при одном и том же объеме n выборки Z_n.

θ1

Δ =

mX ,   θ2

Δ =

σX .

Замечание 2.   Пусть СВ X имеет нормальное распределение N(m_X,σ_X) с неизвестными параметрами

В этом случае выборочное среднее является эффективной оценкой МО.

zn

Δ =

col(x1, x2, ... , xn):

2. Метод максимального правдоподобияНа практике часто удается предсказать вид плотности распределения f_X(x,θ₁, ... , θ_s) непрерывной СВ X с точностью до неизвестных параметров θ₁, ... , θ_s (например θ₁ = m_X, θ₂ = d_X при s = 2), которые требуется оценить по выборке Z_n.Рассмотрим выборку Z_n, соответствующую плотности f_X(x,θ₁, ... , θ_s) СВ X. Функцией правдоподобия называется плотность распределения n-мерной СВ Z_n с реализацией

L(zn,θ1, ... , θs)

Δ =

fZ

n

(zn,θ1, ... , θs)

Л13.Р1.О1       =

n  ∏  k=1

fX(xk,θ1, ... , θs).

Оценкой максимального правдоподобия (ММП-оценкой), найденной по методу максимального правдоподобия, называется оценка

^ θ(Zn),

максимизирующая для каждой реализации z_n функцию правдоподобия:

^ θ(Zn) = arg

max   θ

L(zn,θ),   θ

Δ =

col(θ1, ... , θs) .

Аналогично определяется ММП-оценка θ при неоднородной выборке

Zn

Δ =

col(X1, ... , Xn),

когда СВ X_k, к = 1,n , по-прежнему независимы, но имеют различные плотности распределения f_Xk(x_k,θ₁, ... , θ_s), зависящие от одного и того же набора неизвестных параметров θ₁, ... , θ_s .

3. Метод наименьших квадратовРассмотрим линейную регрессионную модель из предыдущего раздела, не предполагая, что ошибки W_k имеют нормальное распределение, и, кроме того, считая, что коэффициенты X_k случайны:

Yk

Δ =

aXk + b + Wk ,

k = 1,n . Пусть M[W_k] = 0, D[W_k] = σ² и неизвестна, СВ W_k, k = 1,n, независимы. Предположим, что СВ X_k и W_k, k = 1,n, независимы, причем X_k имеют одно и то же, но неизвестное распределение F_X(x). По результатам наблюдений (y₁,x₁),...,(y_n,x_n) требуется оценить неизвестные параметры a и b в линейной регрессионной модели. Для неоднородной выборки

zn

Δ =

col(y1, ... , yn, x1, ... , xn)

рассмотрим квадратическую функцию:

Q(zn,a,b) =

1  n

n  ∑  k=1

(yk - axk - b)2 ,

характеризующую среднюю по n квадратическую ошибку предсказания того, что в n наблюдениях СВ Y примет значения y_k, k = 1,n .

МНК-оценками, полученными по методу наименьших квадратов неизвестных параметров a и b в линейной регрессионной модели

Yk

Δ =

aXk + b + Wk ,

k = 1,n, называются оценки

^ a(Zn) и

^ b(Zn) ,

значения которых минимизируют квадратическую функцию Q(z_n,a,b), построенную по апостериорной выборке z_n.

случае видно, что функция Q(z_n,a,b) совпадает по форме с точностью до коэффициентов с логарифмической функцией правдоподобия из примера Л15.Р2.П1:

Q(zn,a,b) = -2σ2

~ L(zn,a,b) -2σ2n ln(σ√2π).

Поэтому минимум функции Q(z_n,a,b) по параметрам a и b достигается при тех же значениях

^ a и

^ b ,

что и в методе максимального правдоподобия (минимизация функции Q(z_n,a,b) по a и b эквивалентна максимизации функции

~ L(zn,a,b))

^ MX

Найденные по методу наименьших квадратов оценки

^ a(zn) и

^ b(zn)

неизвестных параметров a и b имеют место для произвольных случайных ошибок W_k и случайных коэффициентов X_k, тогда как по методу максимального правдоподобия эти же оценки получены в предположении о нормальности W_k и для детерминированных значений x_k, k =1,n. Иными словами, МНК-оценки оказываются более робастными (т.е. менее чувствительными к априорной информации о случайных коэффициентах X_k и ошибках W_k) по сравнению с ММП-оценками.

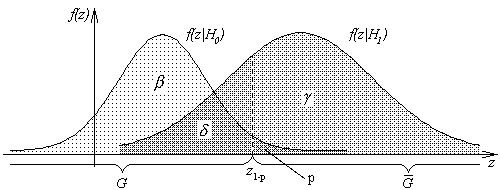
19 Статистическая проверка гипотезСтатистическими гипотезами называются любые предположения относительно закона распределения СВ X, проверяемые по выборке Z_n.По выборке Z_n требуется проверить гипотезу H₀ о том, что m_X= m, где m - некоторое фиксированное число.Статистикой называется произвольная функция Z = φ(Z_n) выборки Z_n, для значений которой известны условные плотности распределения f(z|H₀) и f(z|H₁) относительно проверяемой гипотезы H₀ и конкурирующей с ней альтернативной гипотезы H₁.Из опред следует, что Z есть СВ. Практическое применение математической статистики состоит в проверке соответствия результатов экспериментов предполагаемой гипотезе. С этой целью строится процедура (правило) проверки гипотезы.Критерием согласия называется правило, в соответствии с которым по реализации

z

Δ =

φ(zn)

статистики Z, вычисленной на основании апостериорной выборки z_n, гипотеза H₀ принимается или отвергается. Критической областью G называется область реализаций z статистики Z, при которых гипотеза H₀ отвергается.Доверительной областью G называется область значений z статистики Z, при которых гипотеза H₀ принимается.Уровнем значимости p критерия согласия называется вероятность события, стоящего в том, что гипотеза H₀ отвергается, когда она верна, т.е.

p

Δ =

P{Z G|H0} ,

где вероятность P соответствует условной плотности распределения f(z|H₀). Мощностью γ критерия согласия называется вероятность события, состоящего в том, что гипотеза H₀ отвергается, когда она неверна, т.е.

γ

Δ =

P{Z G|H1} ,

где вероятность P соответствует условной плотности f(z|H₁). Критической точкой z_β называется точка на оси Oz, являющаяся квантилью уровня

β

Δ =

1 - p

распределения F(z|H₀), соответствующего плотности распределения f(z|H₀). На рис.1 показана графическая интерпретация введенных понятий, где β + p = 1, δ + γ = 1.

В качестве критерия согласия примем правило:     1)   если значение

z

Δ =

φ(zn)

статистики Z = φ(Z_n) лежит в критической области G, то гипотеза H₀ отвергается и принимается альтернативная гипотеза H₁;   2)   если реализация

z

Δ =

φ(zn)

статистики Z = φ(Z_n) лежит в доверительной области G, то гипотеза H₀ принимается. При реализации данного правила могут возникнуть ошибки двух видов. Ошибкой 1-го рода называется событие, состоящее в том, что гипотеза H₀ отвергается, когда она верна. Вероятность этой ошибки равна

p

Δ =

P{Z G|H0} .

Ошибкой 2-го рода называется событие, состоящее в том, что гипотеза H₀ принимается, когда она неверна. Вероятность этой ошибки равна

δ

Δ =

P{Z G|H1} = 1 - γ .

Из рисунка видно, что с уменьшением вероятности p ошибки 1-го рода возрастает вероятность ошибки 2-го рода и наоборот, т.е. при выборе критической и доверительной областей должен достигаться определенный компромисс.

Проверка гипотезы о значении параметров нормального распределения Замечание 1.   Пусть известно, что СВ X имеет нормальное распределение. Требуется проверить гипотезу H₀, состоящую в том, что m_X = m (m - некоторое фиксированное число), используя апостериорную выборку z_n. Возможны два случая: дисперсия (σ_X)² известна или неизвестна.

Предполо- жение	Статистика Z критерия согласия	Распре- деление	Доверительная область G принятия гипотезы Н0
σX известно	^ (MX - m)√n       σX	N(0,1)	[-uα , uα]
σX неизвестно	^ (MX - m)√n-1            ^         √DX	S(n-1)	[-tα(n - 1) , tα(n - 1)]

Для каждого случая в соответствии с примерами Л15.Р4.П1 и Л15.Р4.П2 получаем свой критерий согласия. (ниже u_α, t_α(n - 1) - квантили уровня

α

Δ =

1 - p / 2

распределений N(0,1) и S(n-1) соответственно). Пусть СВ X нормально распределена, но ее дисперсия неизвестна. Требуется проверить гипотезу H₀, что σ_X = σ (σ - некоторое фиксированное число), на основе апостериорной выборки z_n. Возможны два случая: m_X - известно или m_X - неизвестно (ниже χ_α(k), χ_1-α(k) - квантили уровня α и 1-α распределения Χ²(k) с k степенями свободы,

α

Δ =

1 - p / 2 для k = n,n-1) :

Предпо- ложение	Статистика Z критерия согласия	Распре- деление	Доверительная область G принятия гипотезы Н0
mX известно	n  ∑(Xk - mX)2  k=1       σ2	Χ2(n)	[-χ1-α(n) , χα(n)]
mX неизвестно	^     nDX        σ2	Χ2(n-1)	[-χ1-α(n-1) , χα(n-1)]

На практике обычно задают p [0.01 , 0.05].

Проверка гипотезы о законе распределения случайной величины Замечание 1.   Пусть имеется апостериорная выборка z_n и требуется проверить гипотезу H₀, состоящую в том, что непрерывная СВ X имеет определенный закон распределения f(x) (например, нормальный, равномерный и т.д.). Истинный закон распределения f(x) неизвестен. Для проверки такой гипотезы обычно используют критерий согласия хи-квадрат (критерий Пирсона). Правило проверки состоит в следующем:     1.   Формулируется гипотеза H₀, состоящая в том, что СВ X имеет плотность распределения определенного вида f(x,θ₁, ... , θ_s) с s неизвестными параметрами θ₁, ... , θ_s(например, m и σ для нормального распределения, a и b - для равномерного и т.д.)     2.   По апостериорной выборке z_n методом максимального правдоподобия (или методом наименьших квадратов) находятся оценки

^ θ1, ... ,

^ θs

неизвестных параметров θ₁, ... , θ_s     3.   Действительная ось R¹ разбивается на j + 1 непересекающихся полуинтервалов Δ₀, ... , Δ_j так, как это сделано в Л13.Р2.31 при построении гистограммы. Подсчитывается число n_k элементов выборки, попавших в каждый полуинтервал Δ_k , k = 1, j-1, кроме Δ₀ и Δ_j.     4.   Вычисляются вероятности p_k попадания СВ X в полуинтервалы Δ_k , k = 0, j , по формуле

pk =

αk+1  ∫ αk

f(x,

^ θ1, .... ,

^ θs) dx ,

где α₀ = -∞, α_j+1 = +∞. Для разрядов Δ_k , k = 1,j-1 значения p_k можно вычислить приближенно по формуле

pk f(xk,

^ θ1, .... ,

^ θs)(αk+1-αk),

где

xk

Δ =

(αk+1 + αk) / 2

- середина разряда Δ_k.     5.   Вычисляется реализация статистики критерия хи-квадрат по формуле

z

Δ =

φ(zn)

Δ = np0 +

j-1  ∑  k=1

(nk-npk)2 / (npk) + (npj) .

    6.   В соответствии с критерием согласия хи-квадрат гипотеза H₀ принимается (т.е. она согласуется с выборкой z_n), если φ(z_n) ≤ χ_1-p(j-s), где χ_1-p(j-s) - квантиль уровня 1-p распределения хи-квадрат с (j-s) степенью свободы, p - заданный уровень значимости (обычно p = 0.05), s - количество неизвестных параметров предполагаемого закона распределения f(x,θ₁, ... , θ_s). Если же φ(z_n) > χ_1-p(j-s), то гипотеза H₀ отвергается. При разбиении на полуинтервалы Δ_k, необходимо учитывать, чтобы np_k ≥ 5 для k = 1, j-1 . В противном случае (np_k < 5) соседние полуинтервалы объединяются.