14. Точечные и интервальные оценки параметров распределения

Пусть (Ω, S, Р), ( где Ω – пространство элементарных событий, S – σ-алгебра, Р – вероятность) вероятностное пространство. Случайную величину Х, определённую на этом пространстве в математической статистике (МС) называют генеральной совокупностью. Исходными данными для любого статистического исследования генеральной совокупности являются результаты n-кратного измерения случайной величины Х. Всюду в дальнейшем будем предполагать, что эти измерения (наблюдения) осуществляются в неизменных условиях и независимо друг от друга. Эти допущения позволяют интерпретировать n-кратное наблюдение случайной величины Х как однократное наблюдение случайного вектора где всеявляются независимыми случайными величинами с одной и той же функцией распределения вероятностей которая совпадает с функцией распределения вероятности генеральной совокупности Тем самым мы приходим к понятию выборки, которая является одним из основных понятий в математической статистике.

Определение 1. Случайной выборкой объёма n при называется случайный вектор

(1)

координаты которогоявляются независимыми случайными величинами с одной и той же функцией распределения вероятностей которая совпадает с функцией распределения вероятности генеральной совокупности Случайные величиныназывают элементами случайной выборки, а саму выборкуназывают случайной выборкой из генеральной совокупности Х.

Определение 2. Реализацией случайной выборки (или просто выборкой) называется неслучайный вектор координатами которого являются реализации соответствующих элементов случайной выборки

Выборку можно рассматривать как совокупностьn чисел

(2)

полученных в результате проведения n повторных независимых наблюдений над генеральной совокупностью Х.

Пусть задана выборка (1) и генеральная совокупность Х, имеющая функцию распределения вероятности, зависящую от параметра .

Пусть (3)

- точечная оценка неизвестного параметра , построенная по выборке (1).

Так как – независимые случайные величины, то точечная оценка (3) как функция случайных величин есть случайная величина. За приближенное значение параметрапринимают реализациюоценки (3), вычисленную по выборке

Оценка (3) называется:

1) несмещенной (без систематических ошибок), если .

2) состоятельной, если сходится к истинному значению параметра по вероятности, то есть

.

3) несмещенная оценка называется эффективной, если у нее по сравнению с другими несмещенными оценками наименьшая дисперсия

.

Пусть – какая-либо точечная оценка неизвестного параметра и пусть найдено число такое, что выполняется равенство

. (4)

Равенство (4) означает, что интервал со случайными границами с вероятностью накрывает неизвестное истинное значение параметра .

При этом интервал называется доверительным интервалом, а вероятность – доверительной вероятностью (обычно выбирают ).

Примеры доверительных интервалов

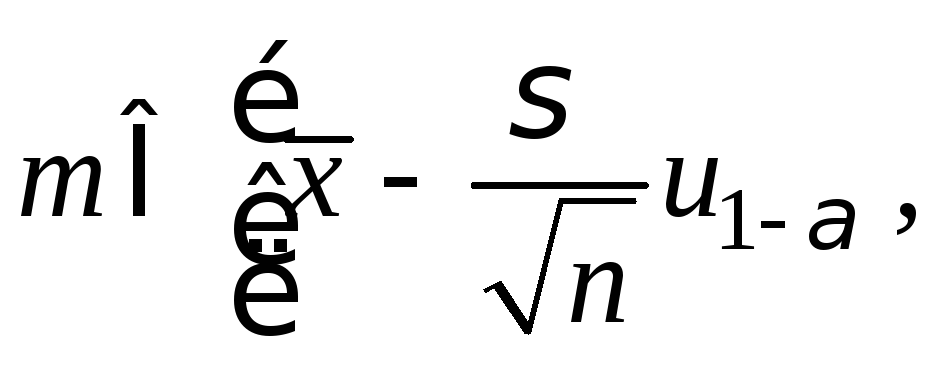
Если генеральная совокупность распределена по нормальному закону m неизвестно, а известно, то с вероятностью где квантиль уровня распределения , , n-объём выборки. Половину длины доверительного интервала в математической статистике называют точностью оценки. Для этого примера точность оценки равна

Если генеральная совокупность m и неизвестны, то с вероятностью

, , ,

где ,  – квантиль распределения Стьюдента (Пирсона) с степенью свободы уровня , – объем выборки. Здесь точность оценки .

Пусть производится серия из независимых испытаний, в каждом из которых событие может произойти с неизвестной вероятностью . В качестве точечной оценки вероятности возьмем частоту , где – объем выборки, а – количество испытаний, в которых событие произошло .

Тогда, если , , , то с вероятностью , где .

Или более точно

.

Здесь точность оценки .

Пример. Найти минимальный объём выборки, при котором с надежностью 0,94 точность оценки математического ожидания нормально распределённой генеральной совокупности (по выборочному среднему ) равна если известно среднее квадратическое отклонение генеральной совокупности

Решение. Для этого примера точность оценки равна

Найдем квантиль По условию Отсюда Подставляя полученные данные в формулу для точности оценки, получим

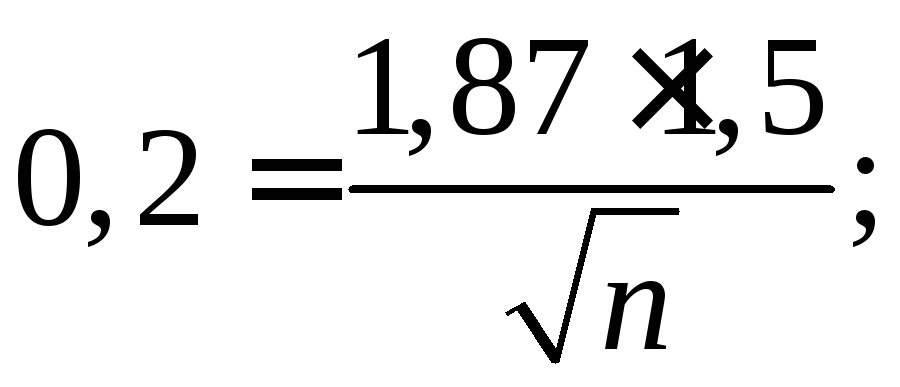
Полагаем

Замечание. При решении задач 92-110 рекомендуем для вычисления квантилей пользоваться их свойствами, приведёнными в п.12.