
- •10. Функции случайных аргументов
- •11. Характеристические функции
- •Свойства характеристических функций
- •Примеры характеристических функций
- •12. Закон больших чисел. Неравенство Чебышева
- •Теорема Чебышева
- •13. Квантили случайных величин
- •Свойства квантилей
- •14. Точечные и интервальные оценки параметров распределения
- •Примеры доверительных интервалов
- •15. Проверка статистических гипотез
- •16. Критерий
10. Функции случайных аргументов
Пусть на
вероятностном пространстве задана
случайная величина
![]() Рассмотрим действительную функцию
действительного аргумента
Рассмотрим действительную функцию
действительного аргумента
![]() ,
область определения которой включает
в себя множество возможных значений
случайной величины x.
,
область определения которой включает
в себя множество возможных значений
случайной величины x.
Случайная величина
![]() действующая
по правилу
действующая
по правилу
![]() называется
функцией
называется
функцией
![]() от скалярной случайной величины x.
от скалярной случайной величины x.
Рассмотрим дискретную случайную величину x, которая задана своим законом распределения вероятностей.
-

x1
x2
…
xn
Р
p1
p2
…
pn
Тогда
![]() имеет закон распределения вероятностей
имеет закон распределения вероятностей
|
h |
φ(x1) |
φ(x2) |
… |
φ(xn) |
|
|
p1 |
p2 |
… |
pn |
При этом, если в верхней строке таблицы появляются одинаковые значения φ(xi), то соответствующие столбцы нужно объединить в один, приписав им суммарную вероятность.
Пример 1.
Закон распределения случайной величины
![]() имеет вид
имеет вид
|
|
–1 |
0 |
1 |
2 |
|
|
|
|
|
|
Найти законы распределения случайных величин:
1)
![]() ,
2)
,
2)
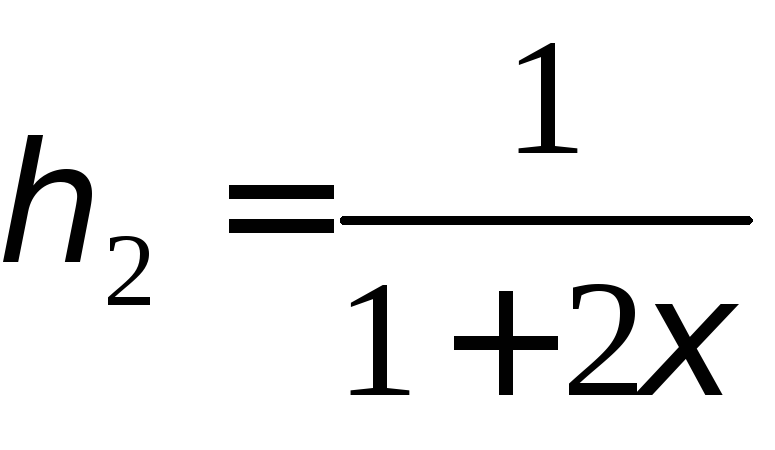 ,
3)
,
3)
![]() .
.
Решение. 1) Возможные
значения случайной величины
![]() найдем, подставив в заданную функцию
возможные значения случайной величины
найдем, подставив в заданную функцию
возможные значения случайной величины
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Вероятности этих значений соответственно равны
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Так как среди
значений
![]() нет повторяющихся, и они расположены в
возрастающем порядке, то закон
распределения случайной величины
нет повторяющихся, и они расположены в
возрастающем порядке, то закон
распределения случайной величины
![]() будет иметь вид
будет иметь вид
|
|
–1 |
1 |
3 |
5 |
|
|
|
|
|
|
2) Возможные значения
случайной величины
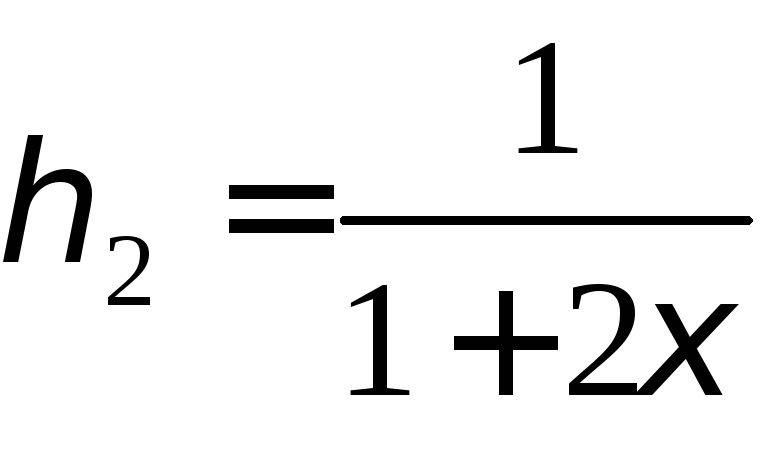 найдем, подставив в заданную функцию
возможные значения случайной величины
найдем, подставив в заданную функцию
возможные значения случайной величины
![]() :
:
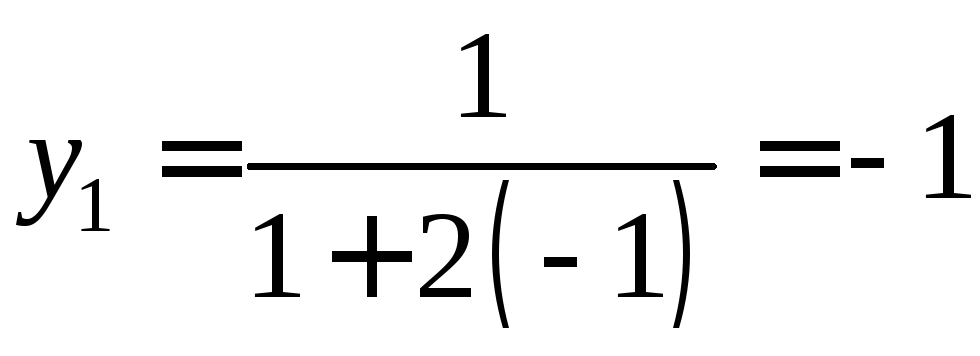 ,
,
![]() ,
,
![]() ,
,
![]() .
Вероятности этих значений соответственно
равны
.
Вероятности этих значений соответственно
равны
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Среди значений
![]() нет повторяющихся, однако они расположены
не в возрастающем порядке. Для получения
закона распределения случайной величины
нет повторяющихся, однако они расположены
не в возрастающем порядке. Для получения
закона распределения случайной величины
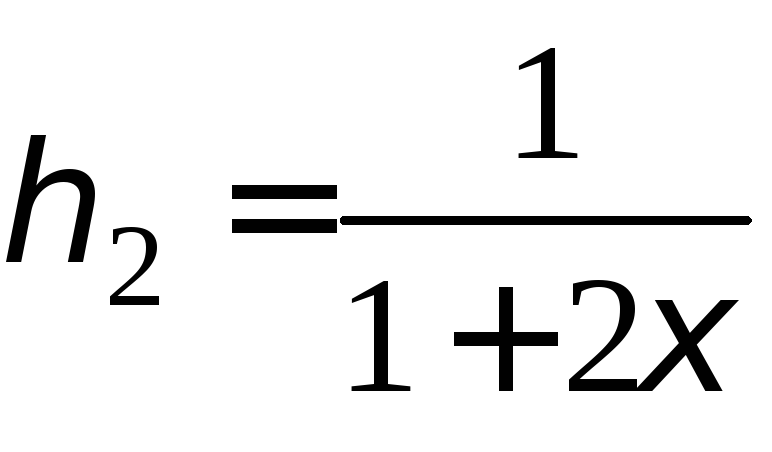 расположим значения
расположим значения
![]() в возрастающем порядке. Закон распределения
случайной величины
в возрастающем порядке. Закон распределения
случайной величины
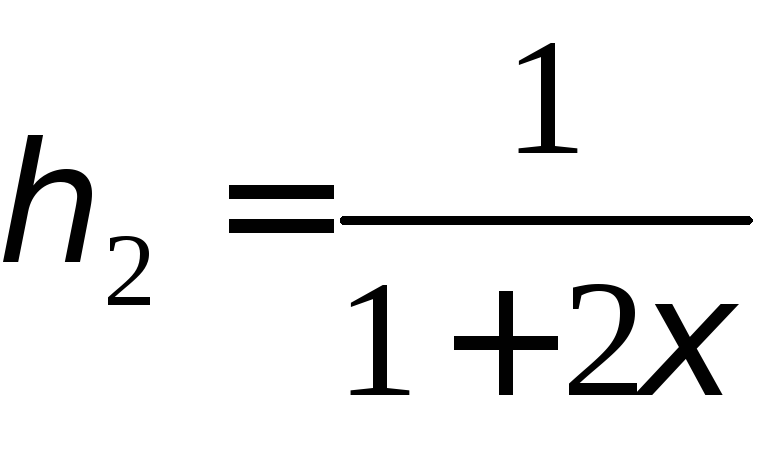 будет иметь вид
будет иметь вид
|
|
–1 |
|
|
1 |
|
|
|
|
|
|
3) Возможные значения
случайной величины
![]() найдем,
найдем,
подставив в заданную
функцию возможные значения случайной
величины
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Вероятности этих значений соответственно
равны
.
Вероятности этих значений соответственно
равны
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Среди значений
![]() есть повторяющиеся
есть повторяющиеся
![]() .
Объединим эти значения в одно, вероятность
которого будет равна сумме вероятностей
.
Объединим эти значения в одно, вероятность
которого будет равна сумме вероятностей
![]() и
и
![]() ,
то есть
,
то есть
![]() .
.
Для получения
закона распределения случайной величины![]() расположим значения
расположим значения
![]() в возрастающем порядке. Ряд распределения
случайной величины
в возрастающем порядке. Ряд распределения
случайной величины
![]() будет иметь вид
будет иметь вид
|
|
2 |
3 |
6 |
|
|
|
|
|
Если
![]() и
и
![]() – независимые дискретные случайные
величины с возможными значениями
– независимые дискретные случайные
величины с возможными значениями
![]() и
и
![]() то
то
![]() может принимать значения
может принимать значения
![]()
![]() Вероятности этих значений равны
Вероятности этих значений равны
![]() .
.
Зная закон
распределения случайной величины
![]() можно по известным формулам найти её
числовые характеристики.
можно по известным формулам найти её
числовые характеристики.
Пример 2.
Независимые случайные величины
![]() имеют законы распределения
имеют законы распределения
|
|
0 |
1 |
2 |
|
|
|
|
|
и
|
|
|
|
|
|
|
|
Найти законы
распределения случайных величин
![]() :
:
а)
![]() ;
б)
;
б)
![]() .
.
Решение. а) Возможные
значения случайной величины
![]()
![]()
![]() –
это
–
это
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
По теореме умножения вероятностей, вероятности этих значений соответственно равны
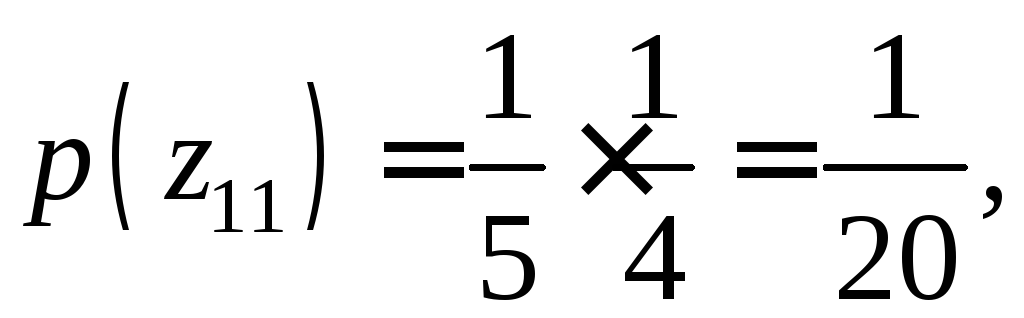
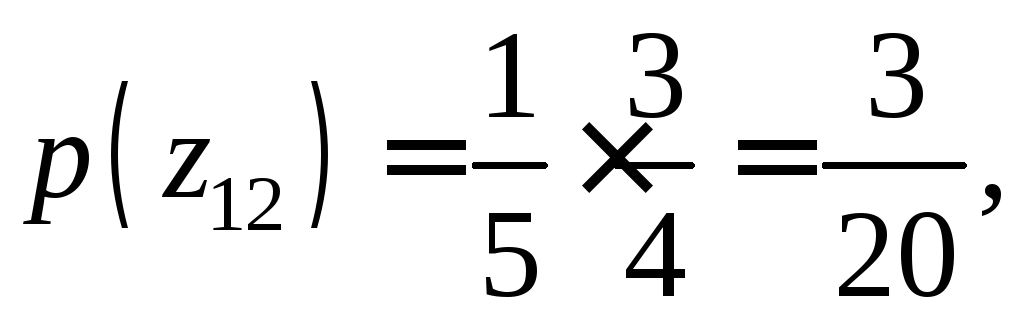
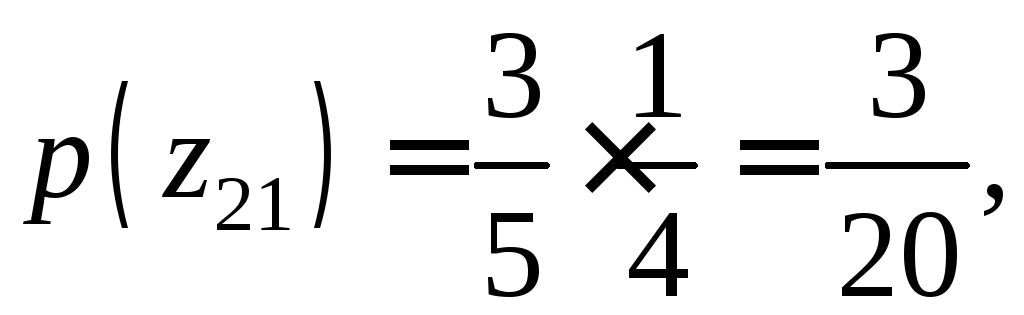
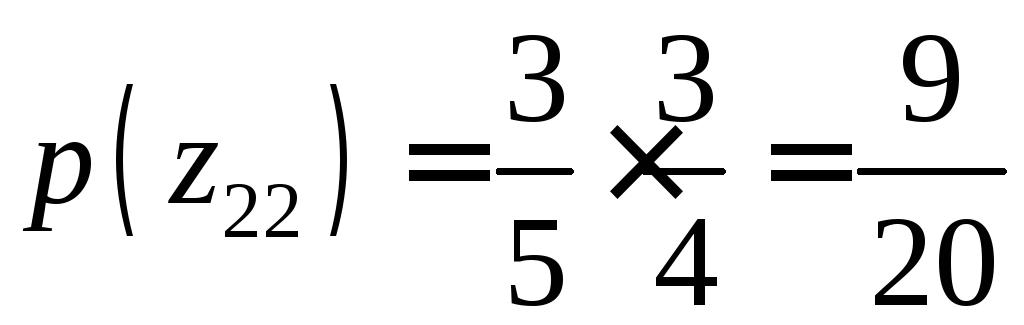 ,
,
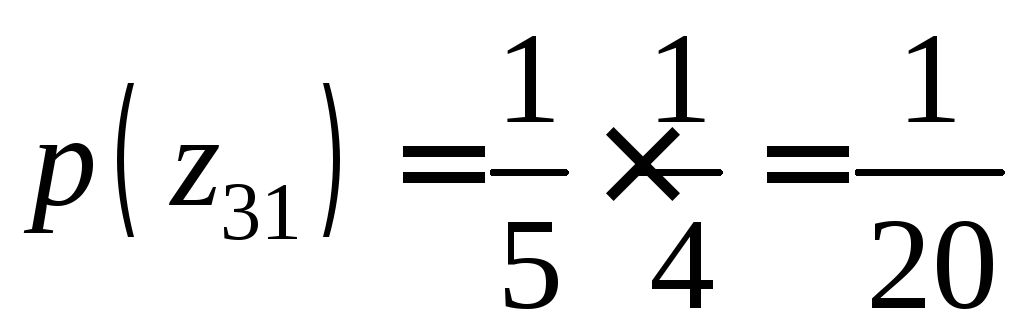 ,
,
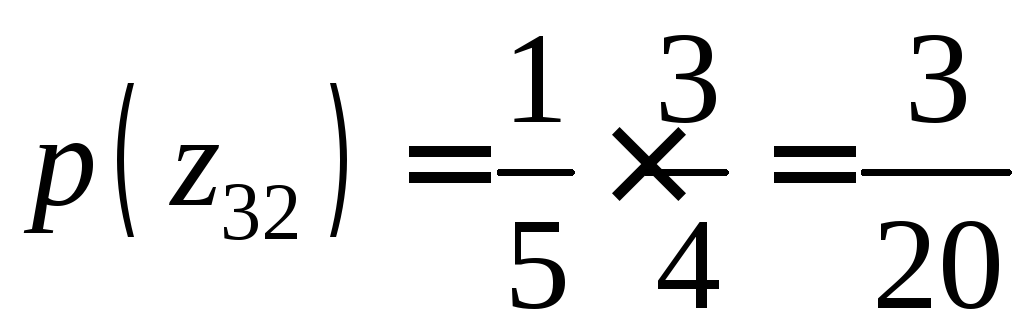 .
.
Составим таблицу
значений
![]() и соответствующих им вероятностей
и соответствующих им вероятностей
-
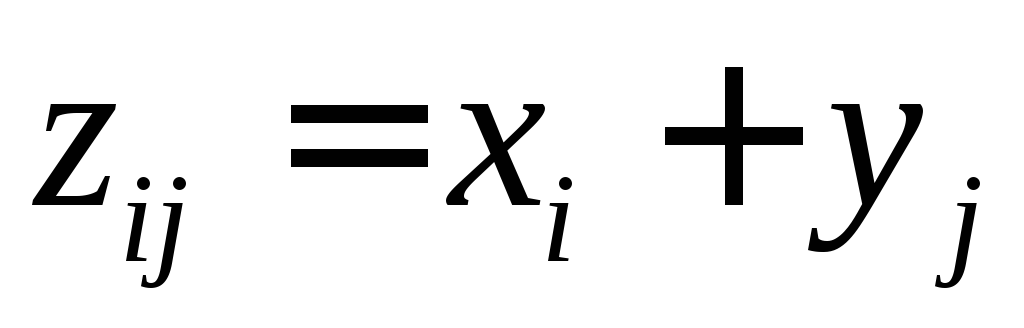
2
4
3
5
4
6
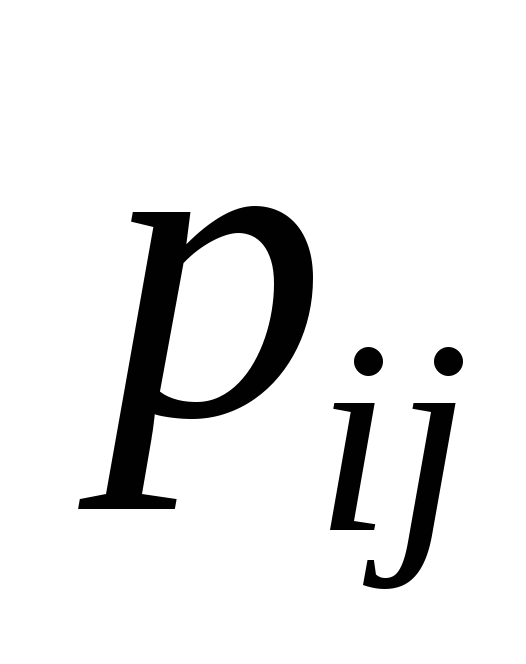
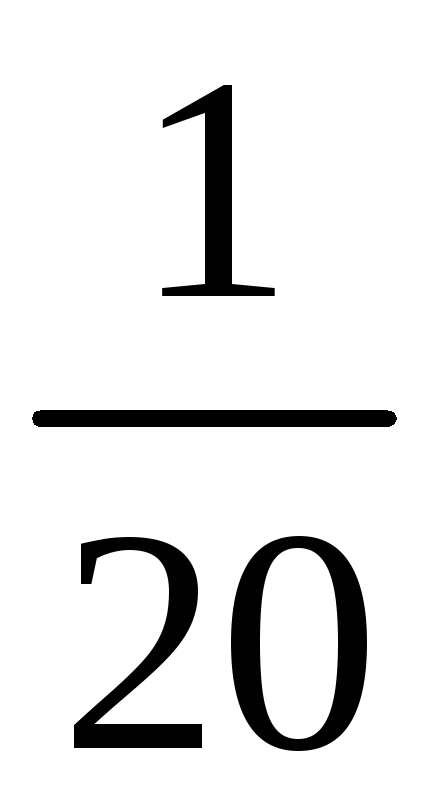

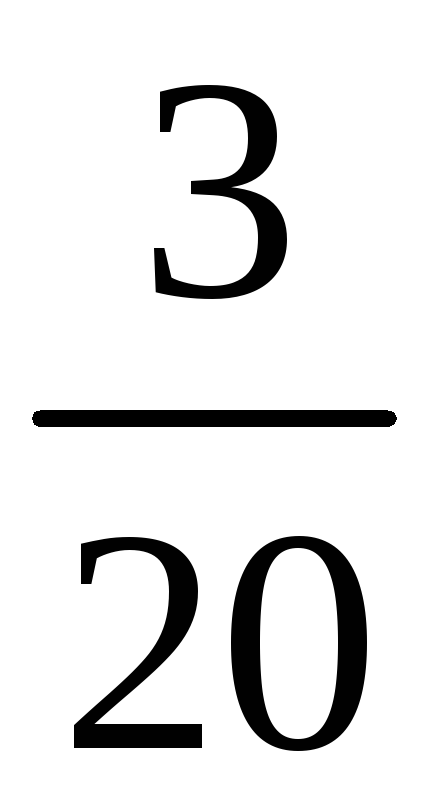
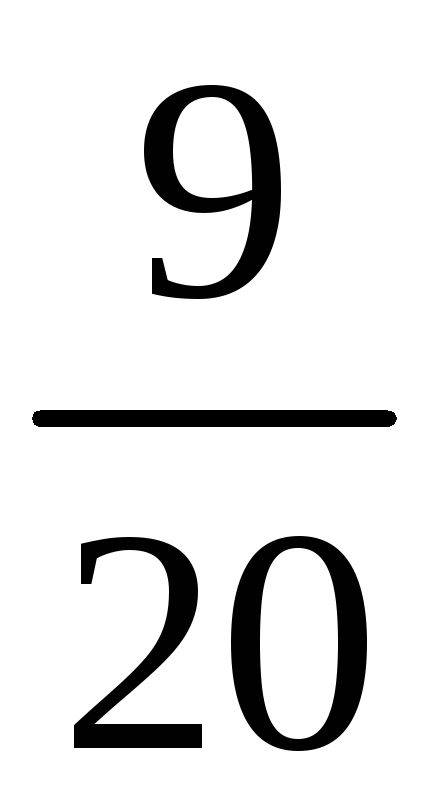
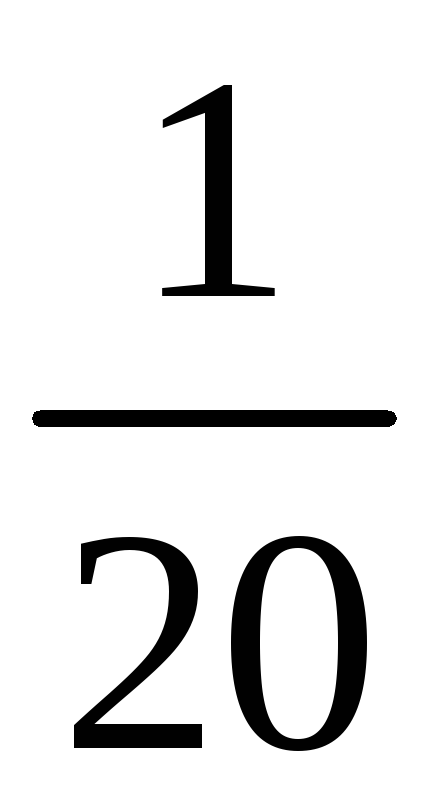
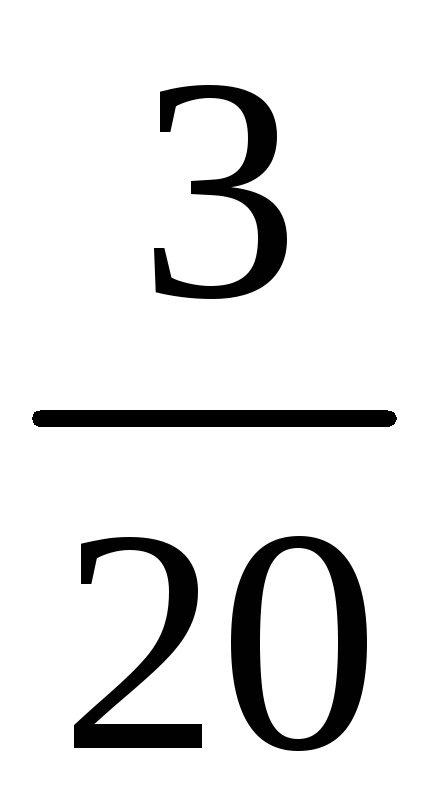
Среди значений
![]() есть повторяющиеся
есть повторяющиеся
![]() .
Объединим эти значения в одно, вероятность
которого будет равна сумме вероятностей
.
Объединим эти значения в одно, вероятность
которого будет равна сумме вероятностей
 и
и
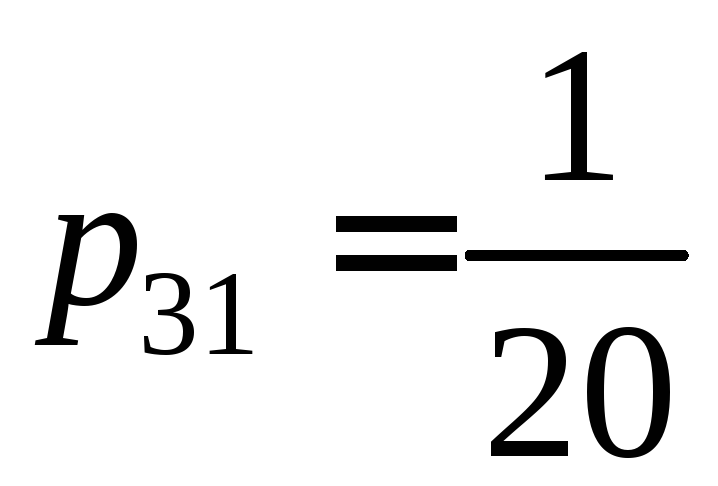 ,
то есть
,
то есть
![]() .
.
Для получения
закона распределения случайной величины![]() расположим значения
расположим значения
![]() в возрастающем порядке. Закон распределения
случайной величины
в возрастающем порядке. Закон распределения
случайной величины
![]() будет иметь вид
будет иметь вид
-
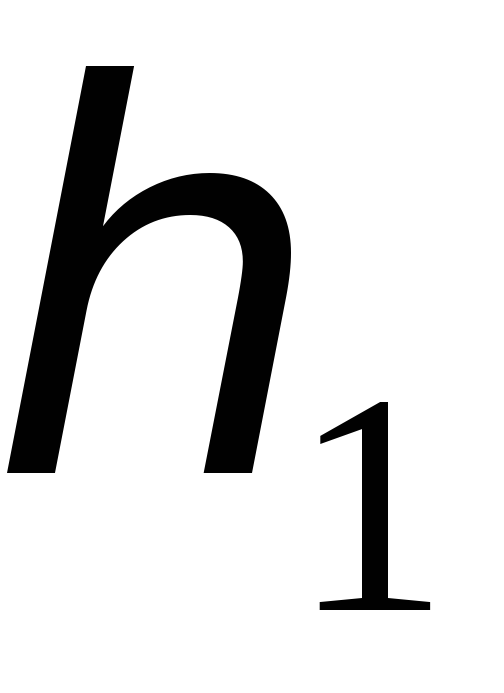
2
3
4
5
6
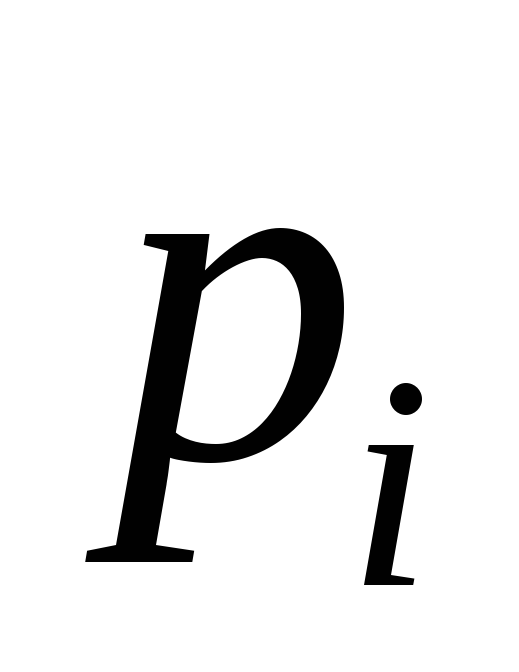
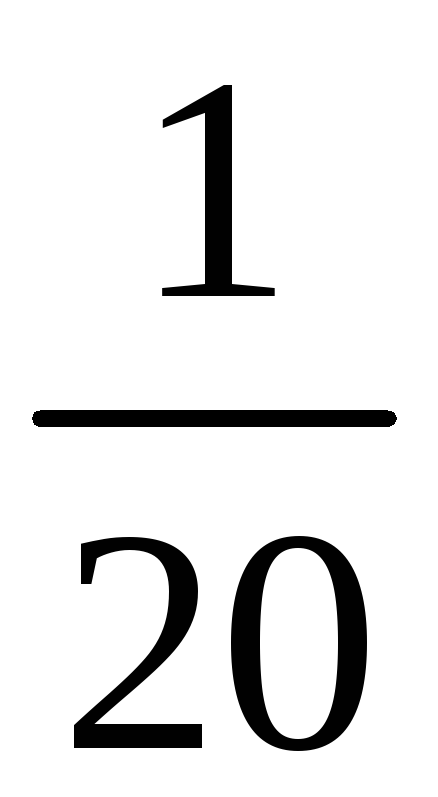
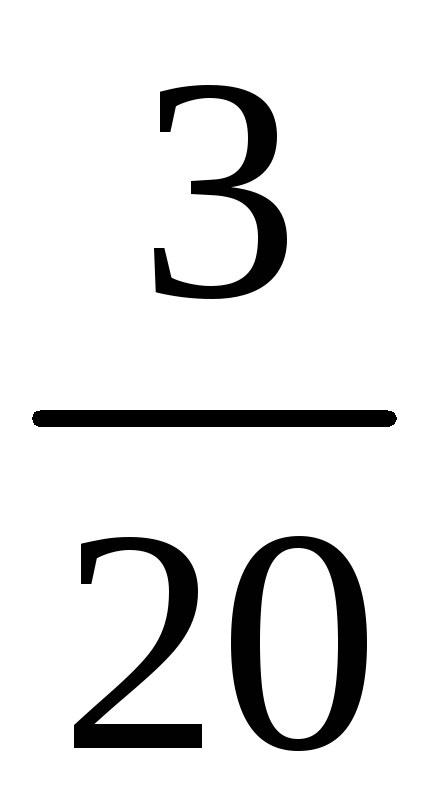
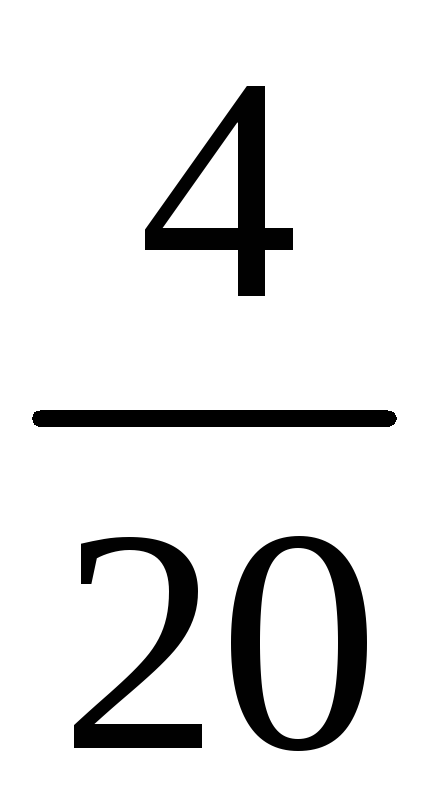
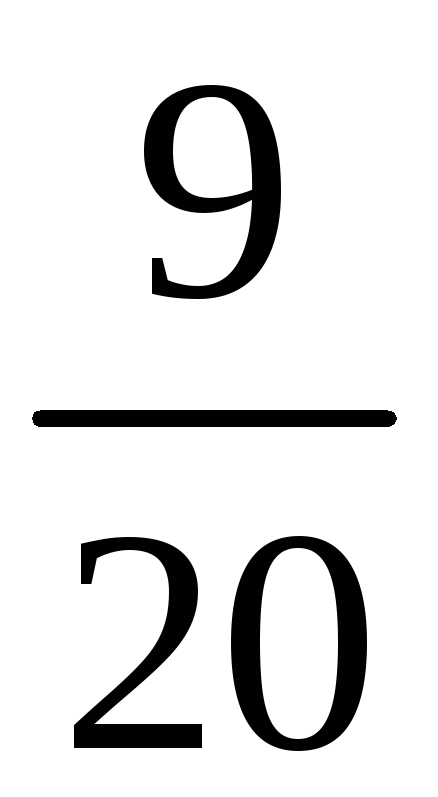
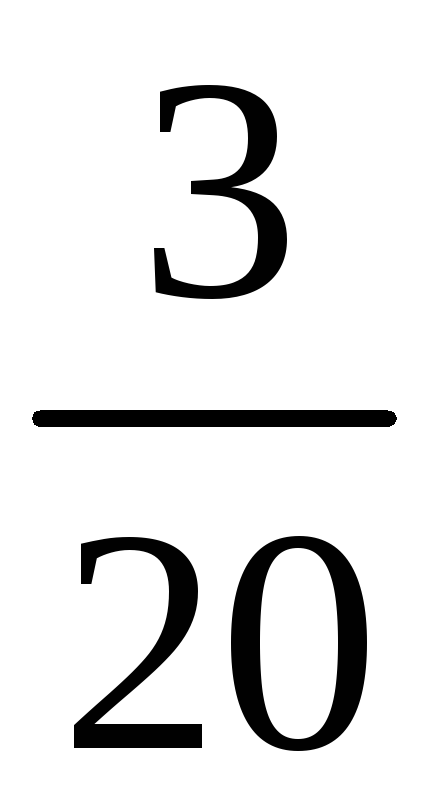
б) Возможные
значения случайной величины
![]()
![]()
![]() –
это
–
это
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
По теореме умножения вероятностей, вероятности этих значений соответственно равны
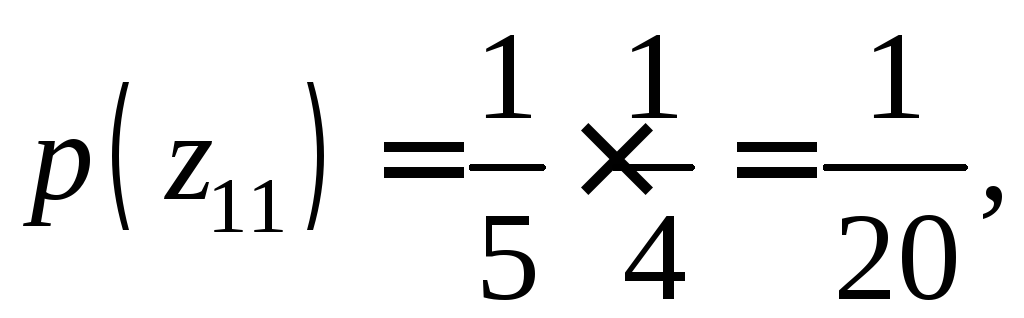

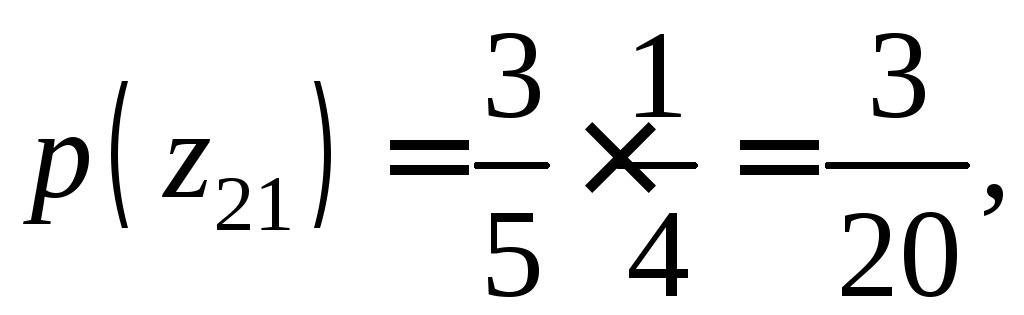
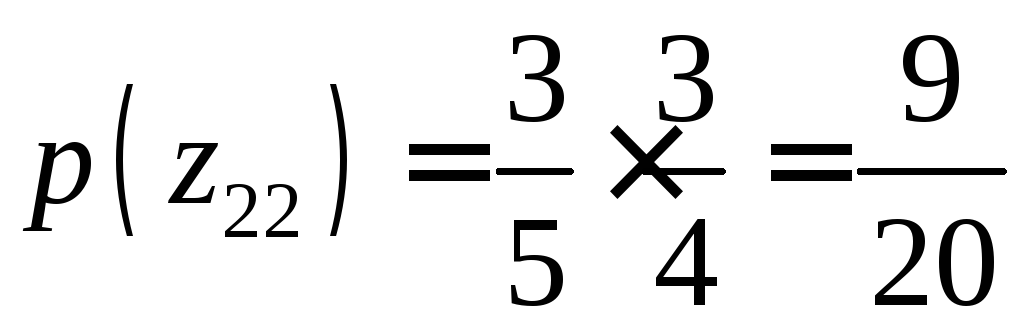 ,
,
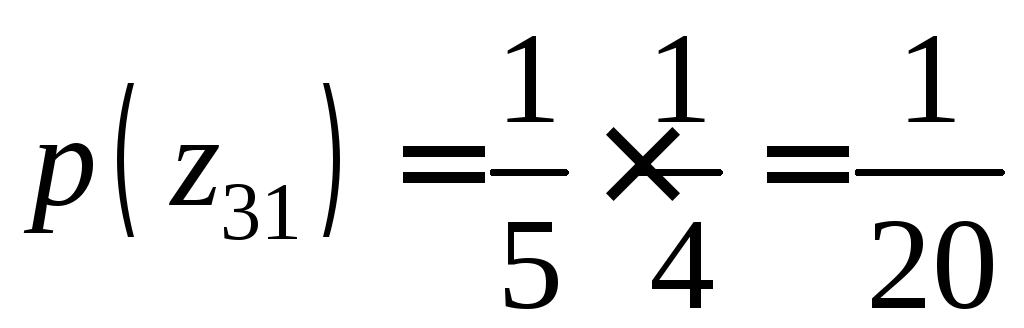 ,
,
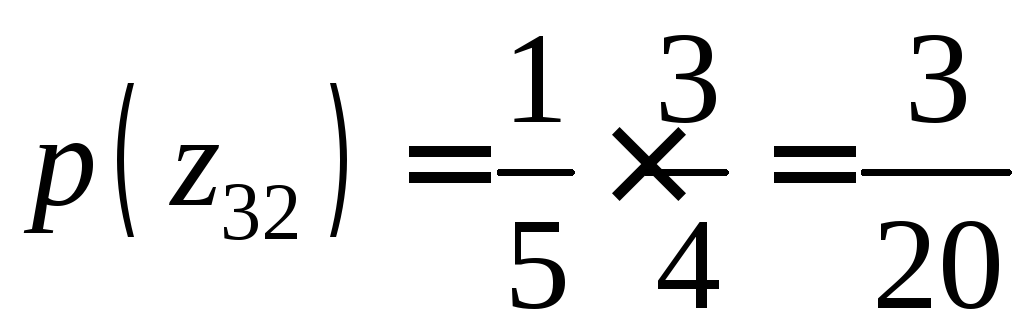 .
.
Составим таблицу
значений
![]() и соответствующих им вероятностей
и соответствующих им вероятностей
-
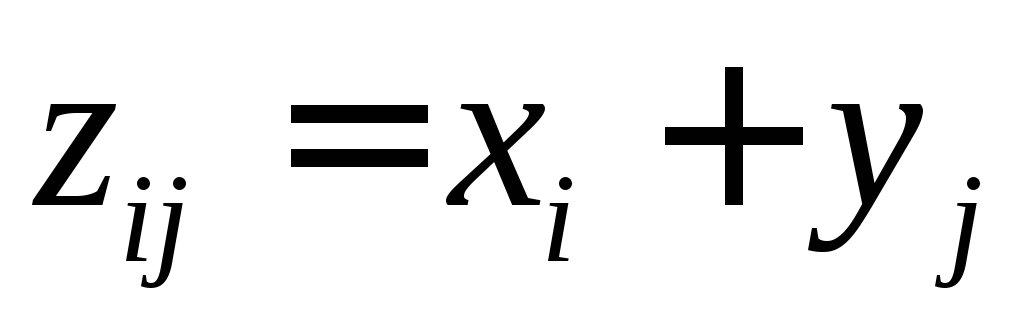
0
0
2
4
4
8
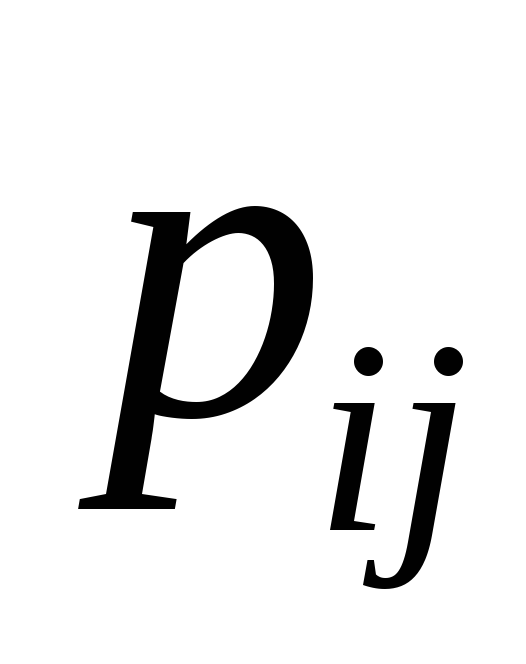
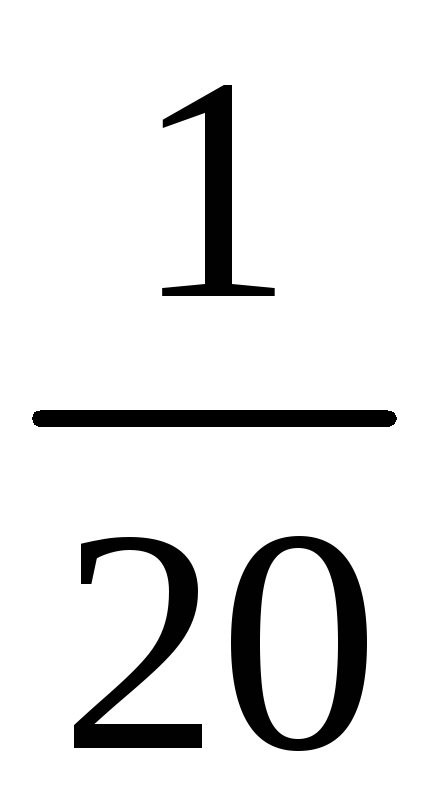
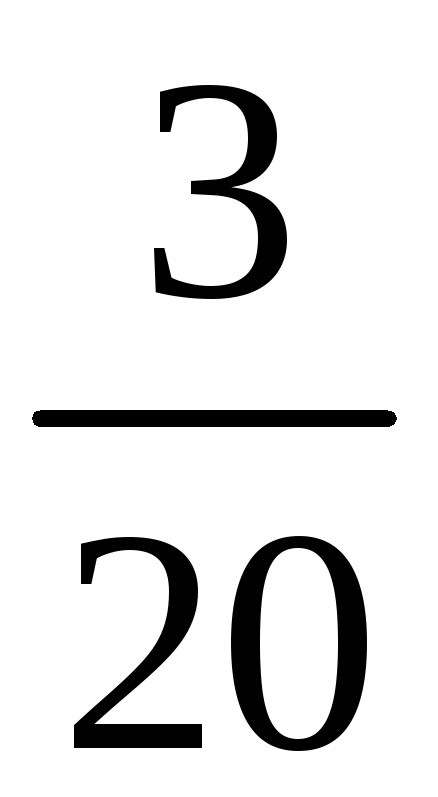
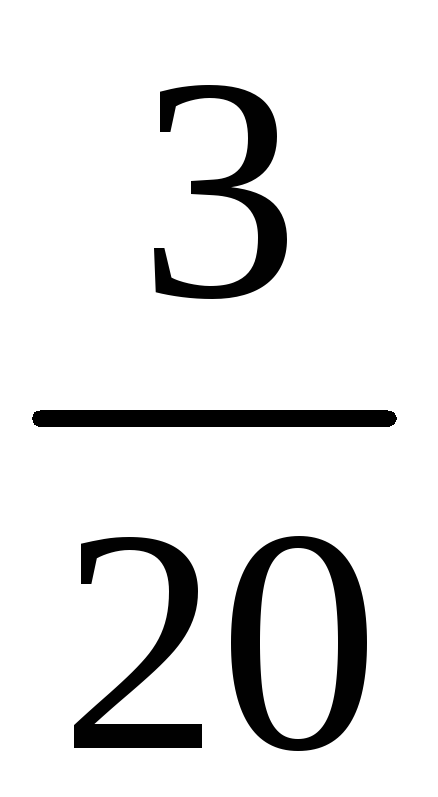
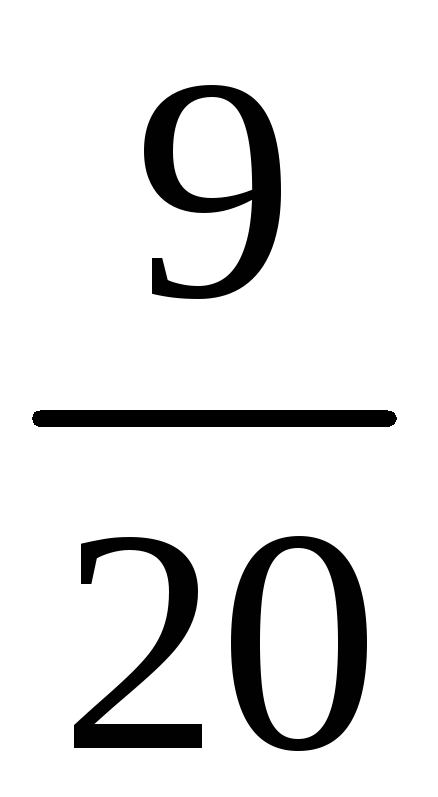
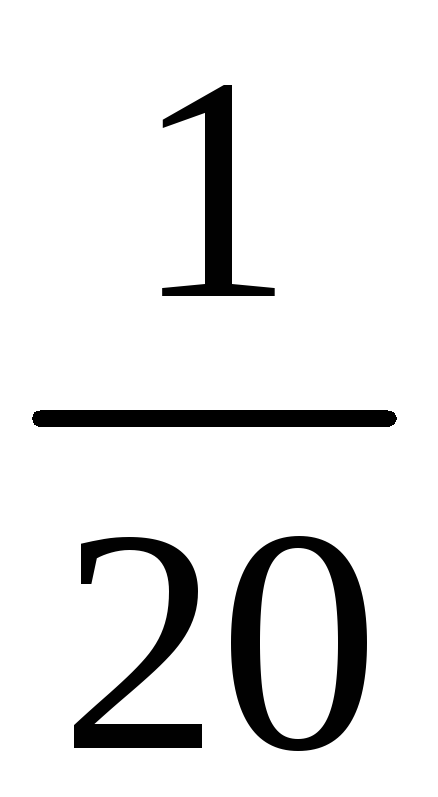

Среди значений
![]() есть повторяющиеся
есть повторяющиеся
![]() и
и
![]() .
Объединим повторяющиеся значения.
Вероятности объединенных значений
будет равна сумме вероятностей
.
Объединим повторяющиеся значения.
Вероятности объединенных значений
будет равна сумме вероятностей
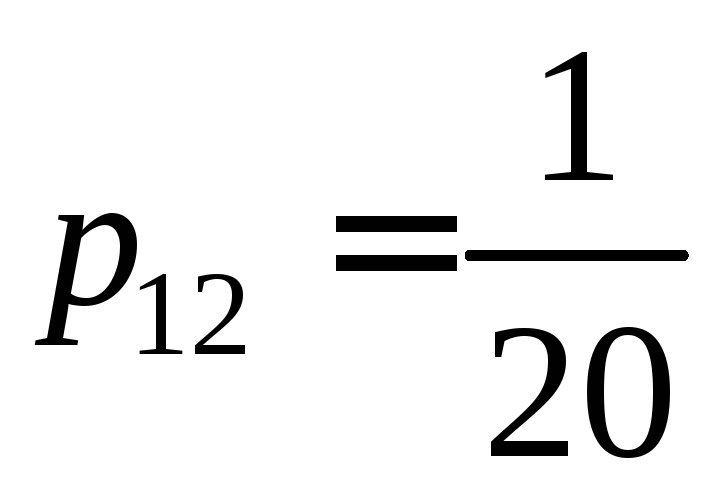 и
и
 ,
то есть
,
то есть
![]() и сумме вероятностей
и сумме вероятностей
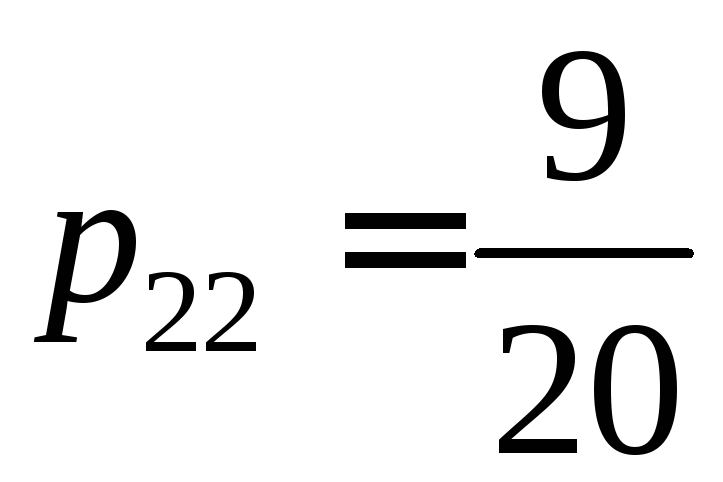 и
и
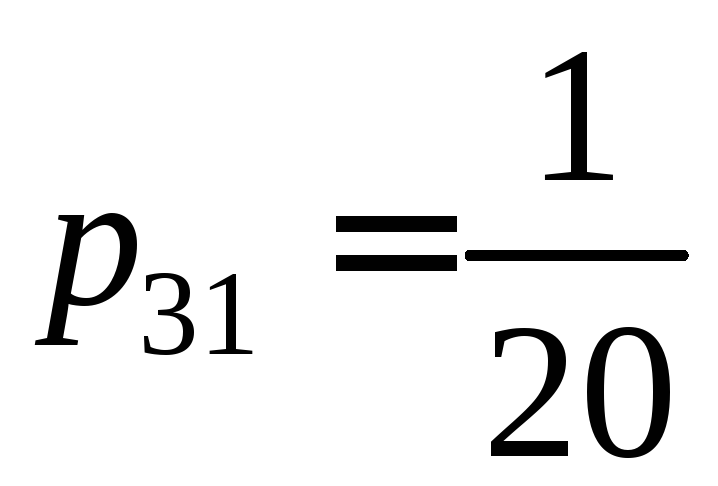 ,
то есть
,
то есть
![]() .
.
Для получения
закона распределения случайной величины![]() расположим значения
расположим значения
![]() в возрастающем порядке. Закон распределения
случайной величины
в возрастающем порядке. Закон распределения
случайной величины
![]() будет иметь вид
будет иметь вид
-
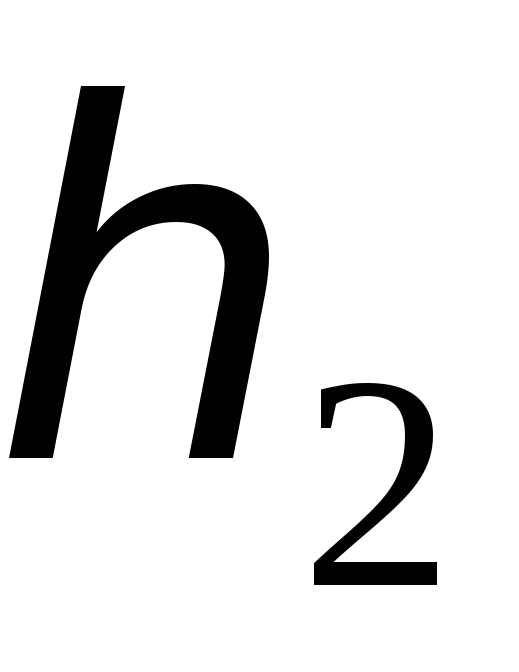
0
2
4
8

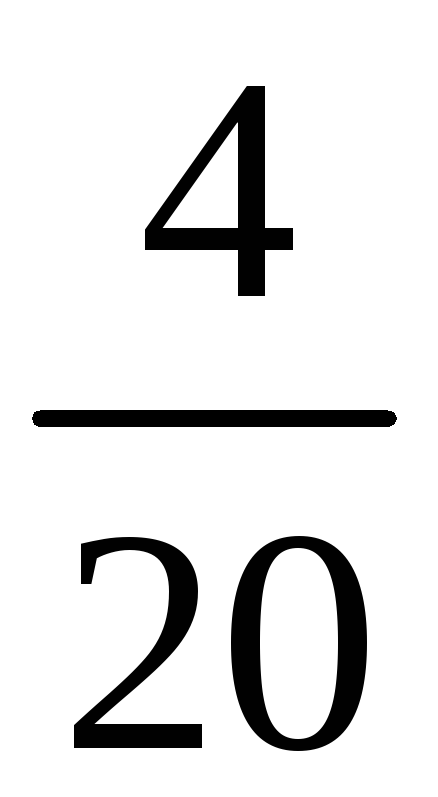


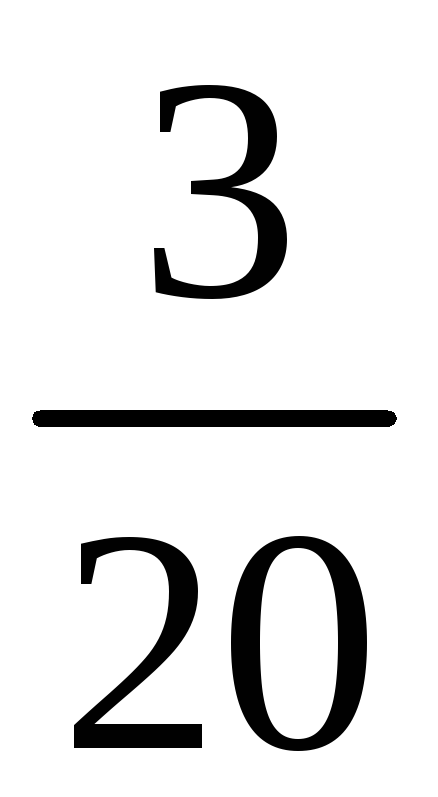
Пример 3. Бросаются
3 монеты. Пусть
![]() ,
если
,
если
![]() я
монета выпала орлом вверх, и
я
монета выпала орлом вверх, и
![]() в противном случае,
в противном случае,
![]() .
Найти закон распределения случайной
величины
.
Найти закон распределения случайной
величины
![]() .
.
Решение. 1. Определяем пространство элементарных исходов.
Элементарными
исходами рассматриваемого случайного
эксперимента являются упорядоченные
наборы чисел
![]() ,
где
,
где
![]() либо нуль, либо единица
либо нуль, либо единица
![]() .
.
2. Определяем
множество возможных значений
![]() .
.
Случайная величина
![]() на элементарном исходе
на элементарном исходе
![]() принимает значение
принимает значение
![]() .
.
3. Составляем
таблицу элементарных исходов и
соответствующих им значений
![]() .
.
|
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
–1 |
2 |
0 |
0 |
1 |
4. Определяем
вероятности возможных значений
![]() и строим ее закон распределения.
и строим ее закон распределения.
Всего элементарных
исходов
![]() .
Следовательно, вероятность элементарного
исхода равна
.
Следовательно, вероятность элементарного
исхода равна
![]() .
Имеем
.
Имеем
|
|
–1 |
0 |
1 |
2 |
|
|
|
|
|
|
Рассмотрим случай непрерывных случайных величин.
Пусть задана
n-мерная
случайная величина
![]() с плотностью распределения вероятности
с плотностью распределения вероятности
![]() и задана функция
и задана функция
![]() .
Чтобы определить случайную величину
.
Чтобы определить случайную величину
![]() необходимо уметь вычислять вероятности
необходимо уметь вычислять вероятности
![]() для любых
для любых
![]() .
Обозначим через D
– множество точек
.
Обозначим через D
– множество точек
![]() .
.
Тогда получим
![]() .
.
Определение. Скажем,
что случайная величина
![]() ,
если для любых
,
если для любых![]() ,
,
![]()
Рассмотрим уравнение
![]() где
где
![]() дифференцируемая функция и пусть
дифференцируемая функция и пусть
![]() ,
,
![]() – функции, обратные к функции
– функции, обратные к функции
![]() .
.
Тогда
![]() ;
;
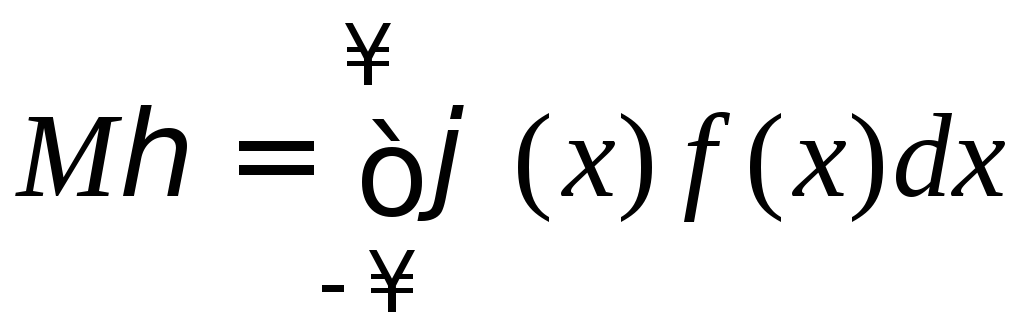 ;
;
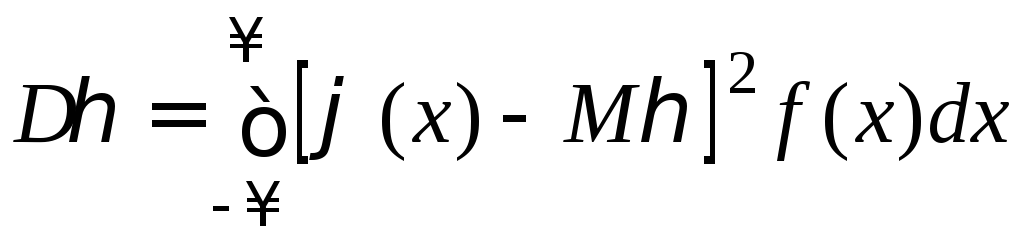 ;
;
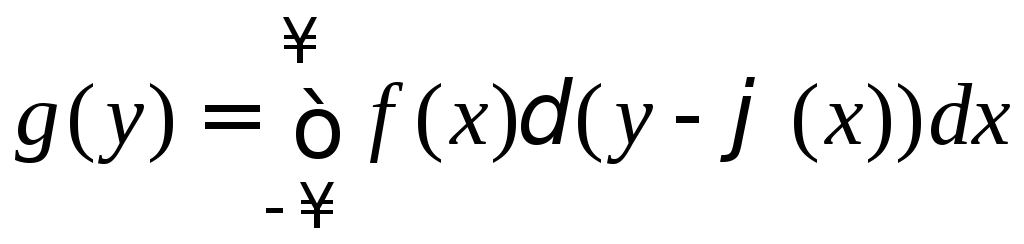 .
.
Для случайного
вектора
![]() с плотностью распределения
с плотностью распределения
![]() ,
если
,
если
![]() ,
то
,
то
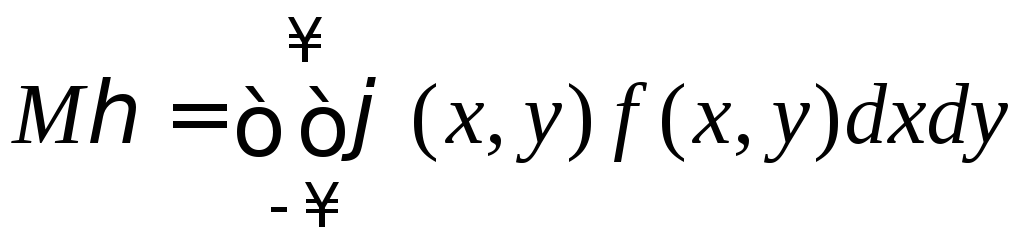 .
.
Примеры функций случайных аргументов.
Распределение
Пирсона
![]() с
с
![]() степенями свободы.
Пусть
степенями свободы.
Пусть
![]() и независимы. Тогда
и независимы. Тогда
![]() имеет плотность распределения
имеет плотность распределения
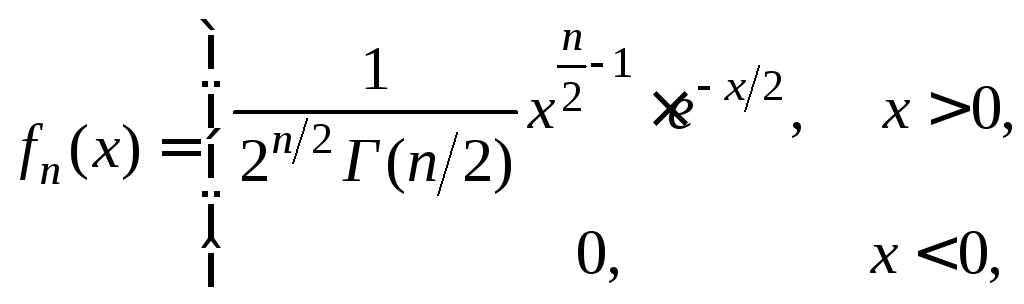
где
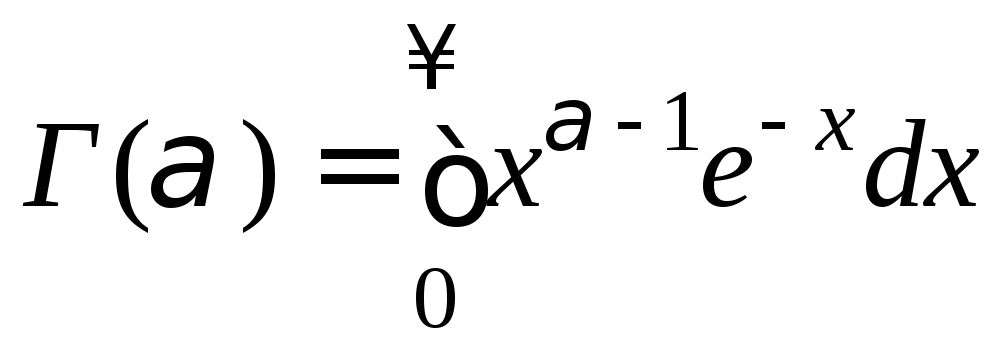 – гамма-функция.
– гамма-функция.
![]() ,
, ![]() .
.
Распределение
Стьюдента с
![]() степенями свободы
степенями свободы
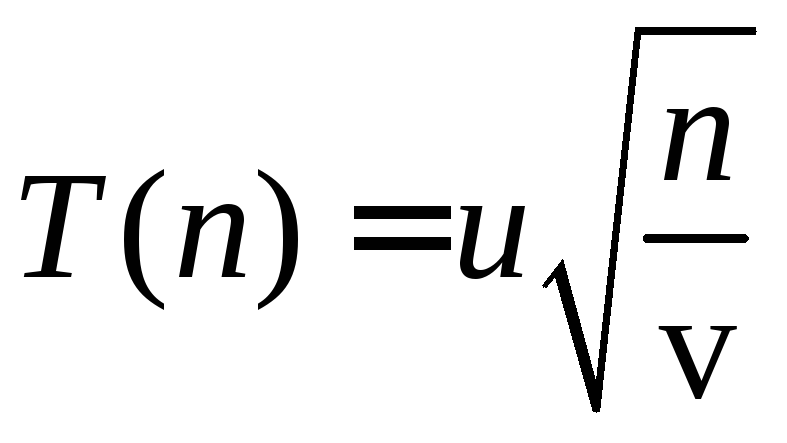 ,
,
где
![]() ,
,
![]() ,
,
![]() – независимые случайные величины, имеет
плотность распределения
– независимые случайные величины, имеет
плотность распределения
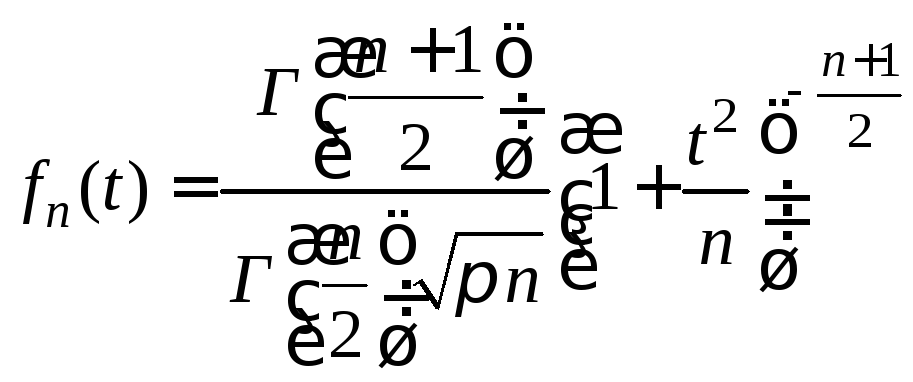 ;
;
![]() ,
, ![]() ,
, ![]() .
.
Пример 4.
Случайная величина
![]() равномерно распределена на отрезке
равномерно распределена на отрезке
![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() ,
где
,
где
 ,
,
![]() .
.
Решение. Так
как случайная величина
![]() равномерно распределена на отрезке
равномерно распределена на отрезке
![]() ,
то
,
то
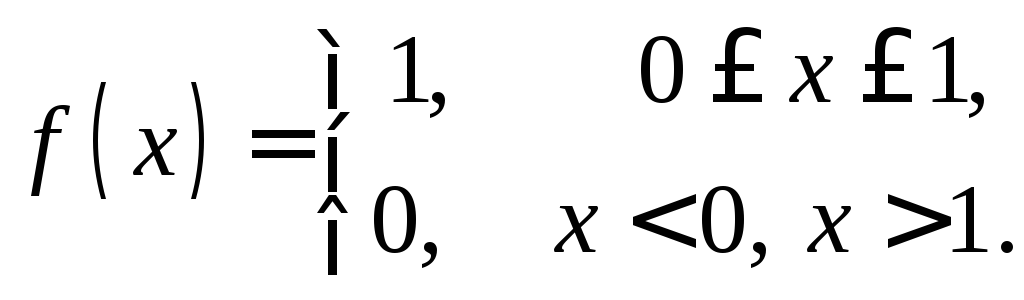
Следовательно,
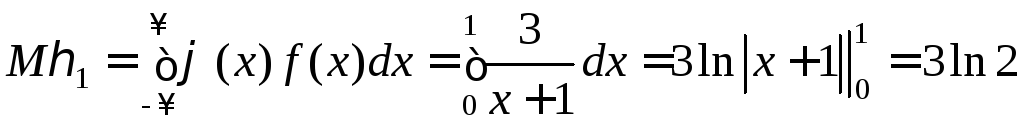 .
.
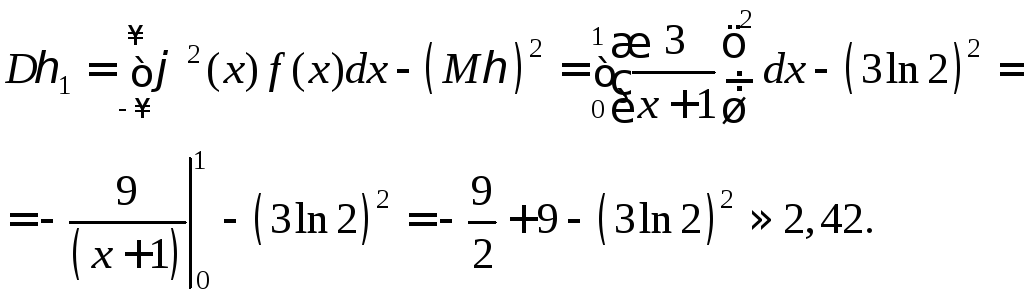
![]() .
.
Аналогично найдем
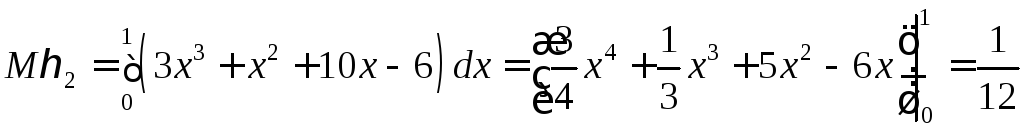 .
.
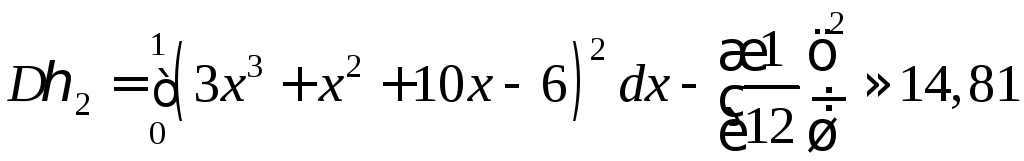 ,
,
![]() .
.
Пример 5. Случайная
величина
![]() распределена по экспоненциальному
закону с параметром
распределена по экспоненциальному
закону с параметром
![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() ,
где,
,
где,
![]() ,
,
![]() .
.
Решение. По условию параметр экспоненциального распределения равен 4, следовательно,

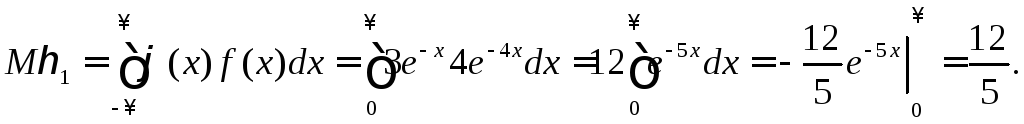

![]() .
.
Аналогично найдем
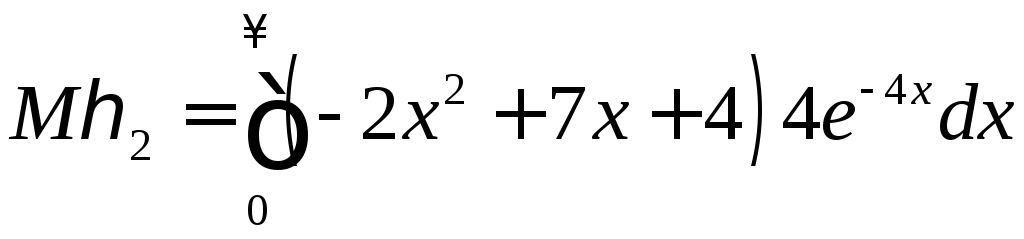 .
Дважды интегрируя по частям, получим
.
Дважды интегрируя по частям, получим
 .
.
Пример 6.
Плотность
распределения случайной величины
![]() равна
равна
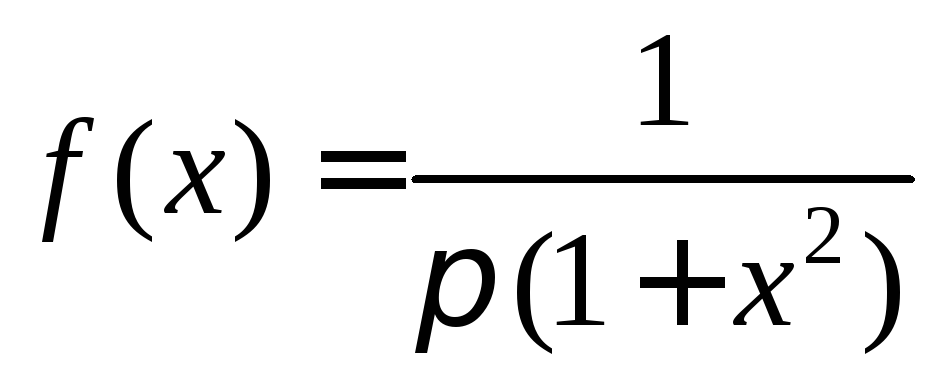 .
Найти плотность распределения
.
Найти плотность распределения
![]() случайной величины
случайной величины
![]() .
.
Решение.
Так как функция
![]() строго возрастающая при всех
строго возрастающая при всех
![]() и имеет обратную, то плотность распределения
и имеет обратную, то плотность распределения
![]() случайной
величины
случайной
величины
![]() найдем по формуле
найдем по формуле
![]()
Для этого находим
![]() ,
,
![]() Подставляем эти выражения в формулу,
представляющую решение задачи в общем
виде. То есть плотность распределения
случайной величины
Подставляем эти выражения в формулу,
представляющую решение задачи в общем
виде. То есть плотность распределения
случайной величины ![]() будет равна
будет равна
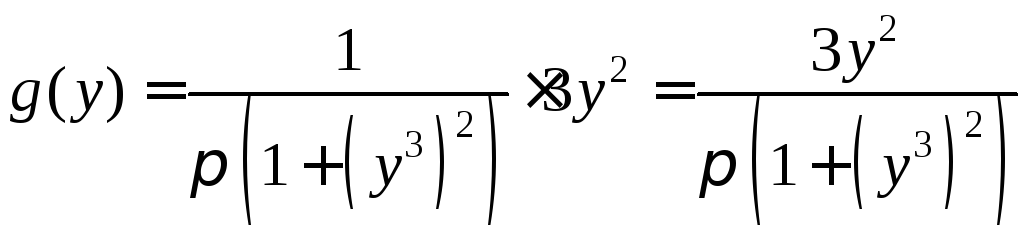 .
.
Пример 7.
Плотность
распределения случайной величины
![]()
равна
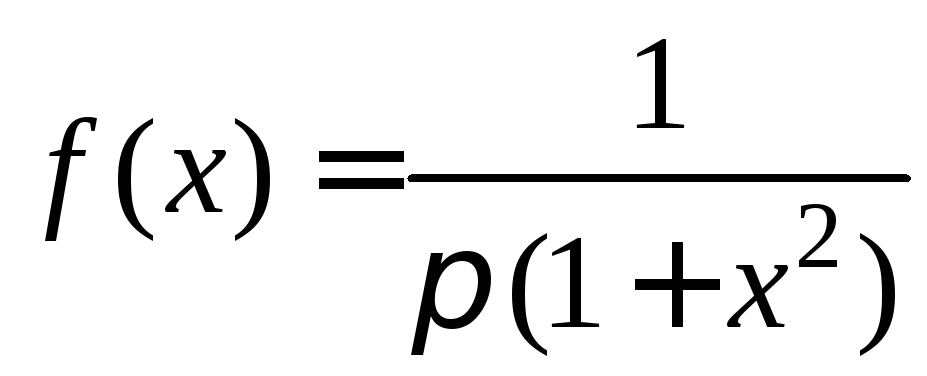 .
Найти плотность распределения
.
Найти плотность распределения
![]() случайной величины
случайной величины
![]() .
.
Решение. 1
способ. Решение
задачи располагаем в виде двух столбцов:
слева будем писать обозначения функций,
принятые в общем случае; справа –
конкретные функции, соответствующие
данному примеру. Учитывая, что, несмотря
на разрывный характер функции
![]() обратная функция
обратная функция![]() однозначна, и решая задачу по правилам
для монотонной функции, получаем:
однозначна, и решая задачу по правилам
для монотонной функции, получаем:
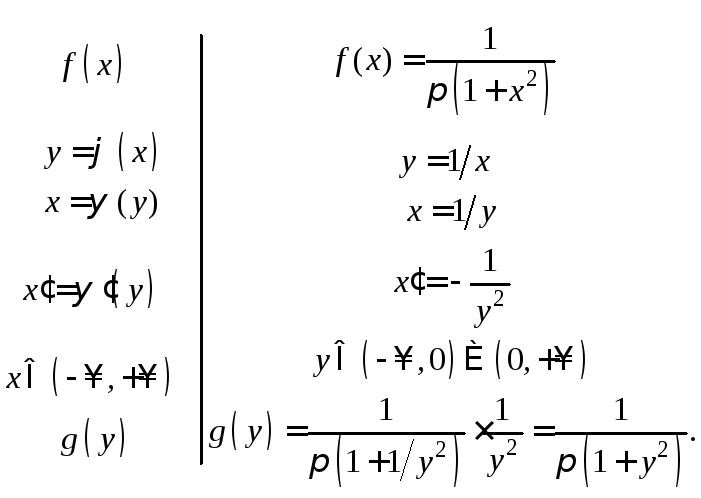
2 способ.
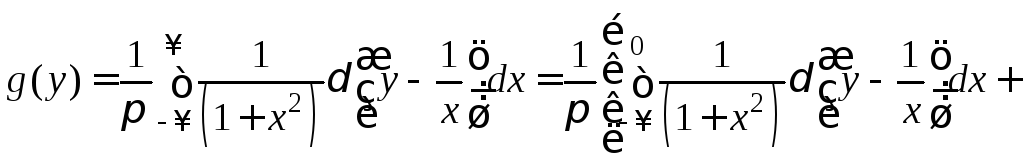
![]()
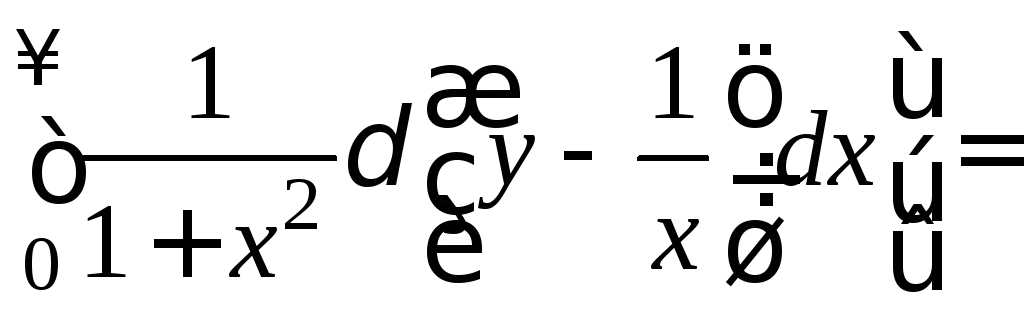
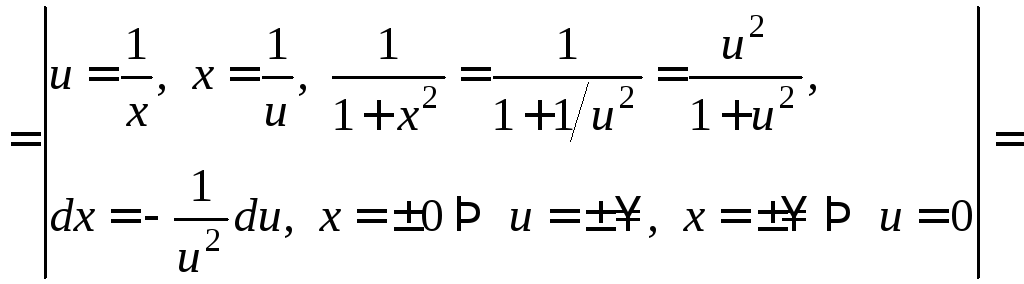

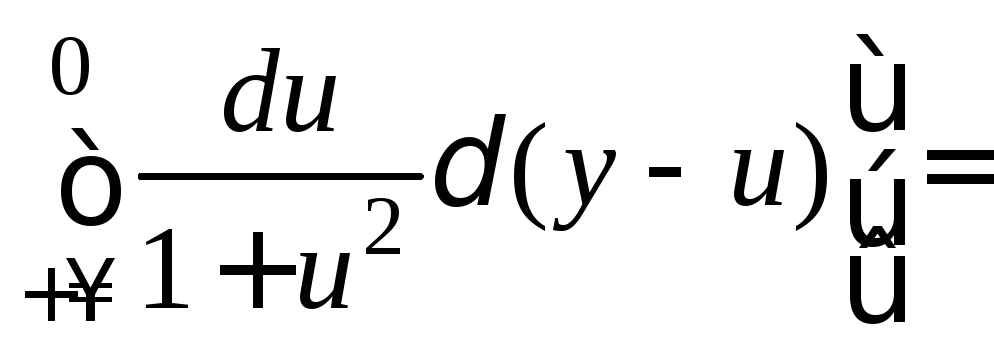
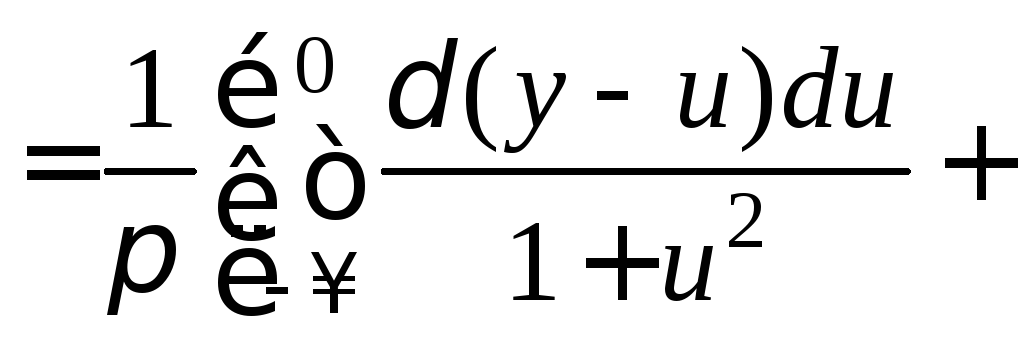
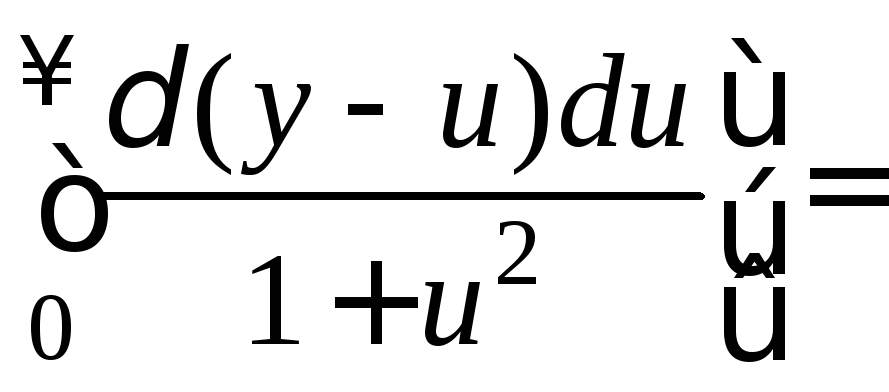
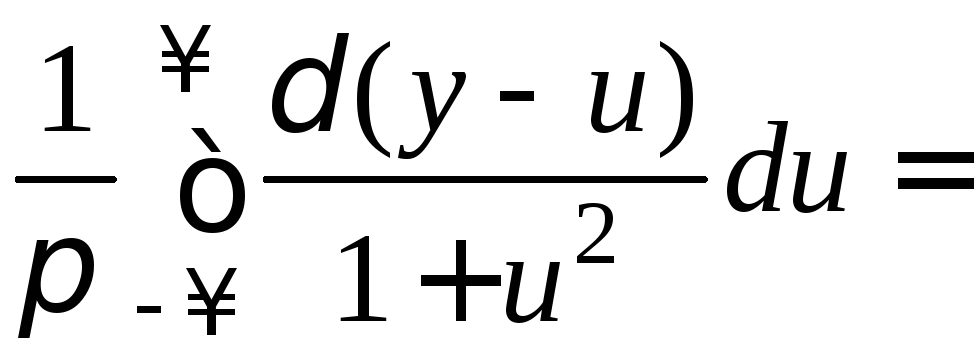
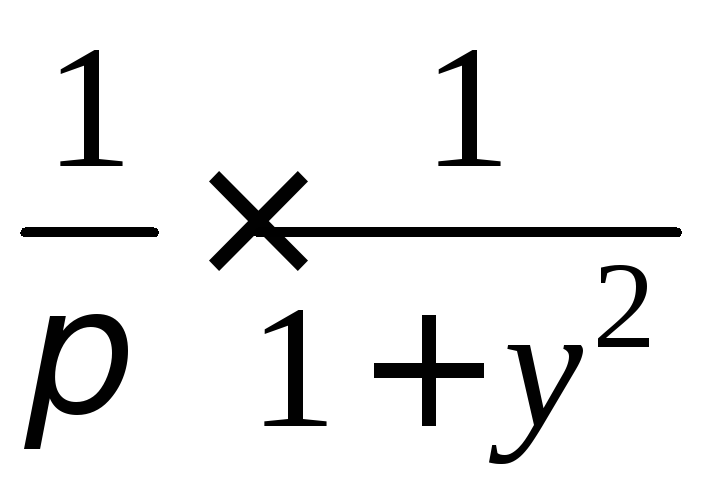 .
.
Пример 8. Случайная
величина
![]() распределена равномерно на интервале
[0,2].
распределена равномерно на интервале
[0,2].
Функция
![]() задана графически
задана графически

Рис. 3
Найти плотность
распределения вероятности
![]() случайной величины
случайной величины
![]() .
.
Решение. В
данном случае функцию
![]() аналитически
можно задать следующим образом:
аналитически
можно задать следующим образом:
![]() или
или
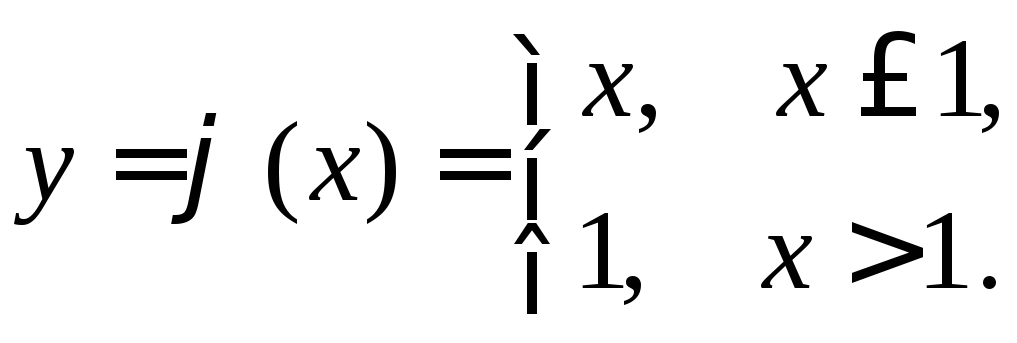
Плотность
распределения случайной величины
![]() имеет вид
имеет вид
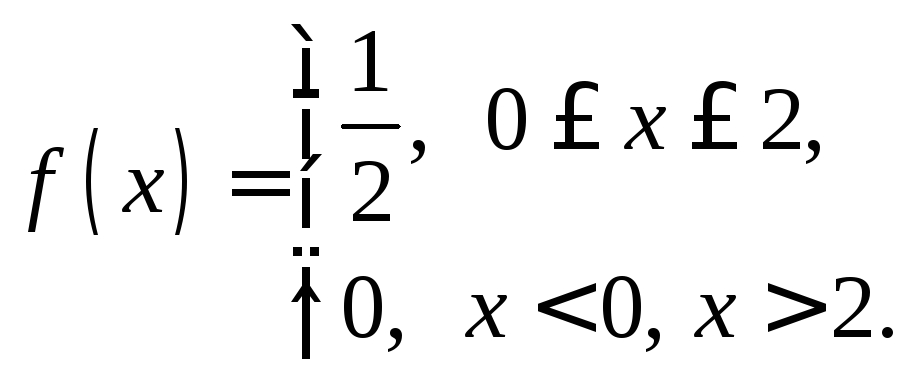
Для нахождения
![]() воспользуемся формулой
воспользуемся формулой
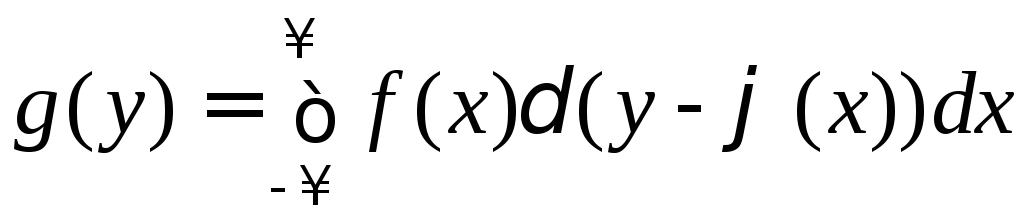 .
Тогда
.
Тогда
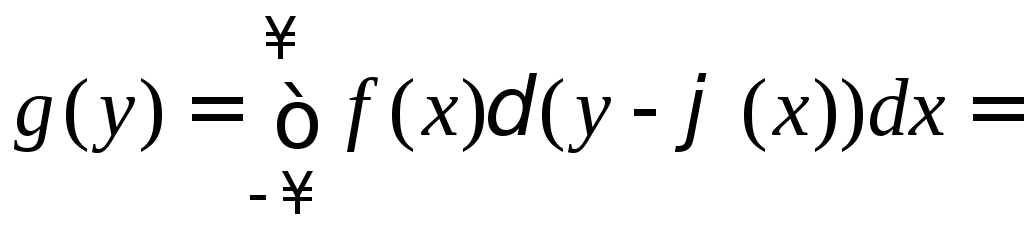
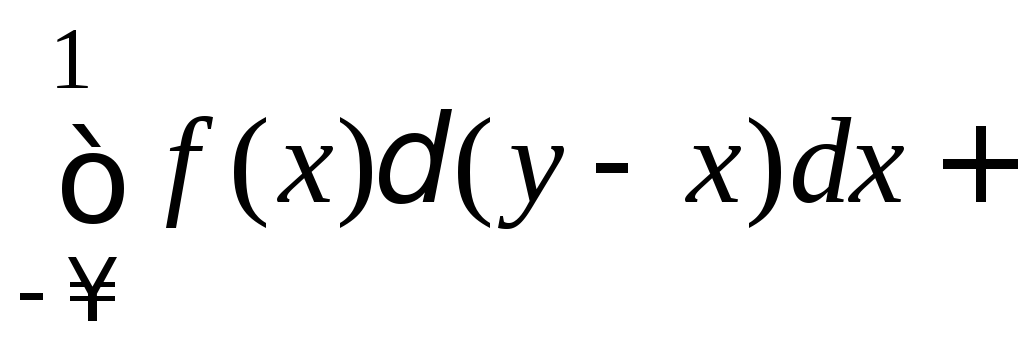

=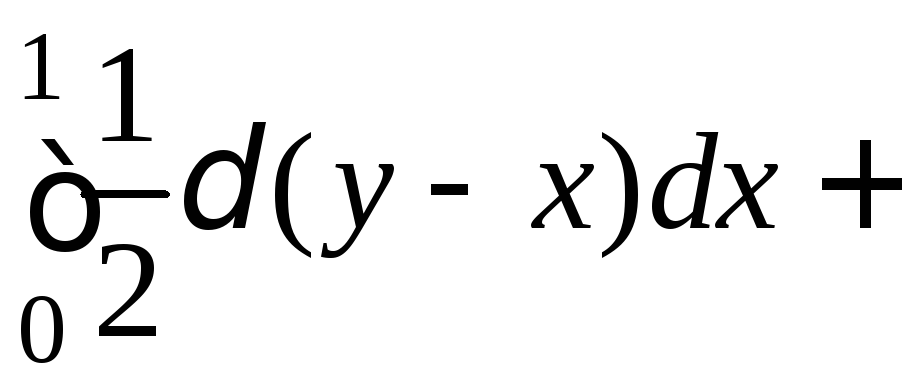
 =
=![]()
 .
.
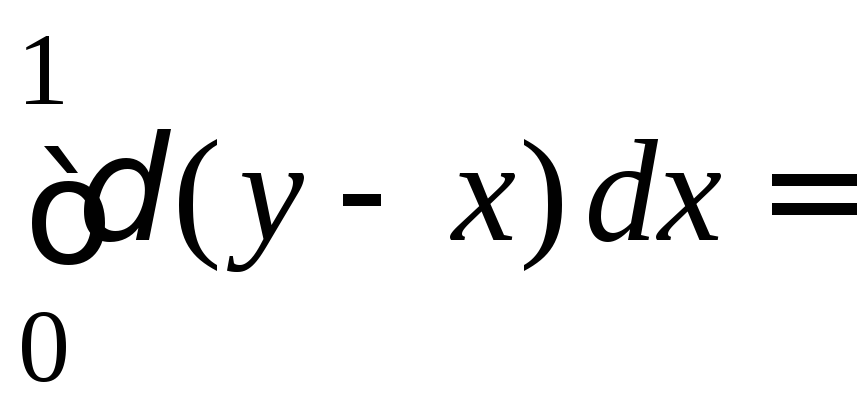
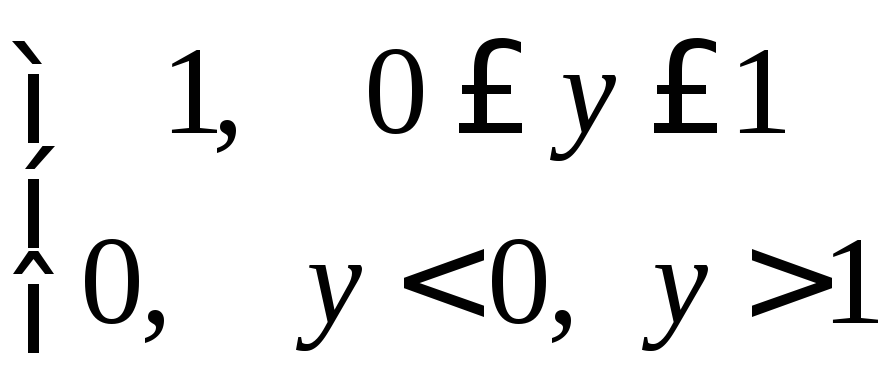 =
=![]() ,
,
где
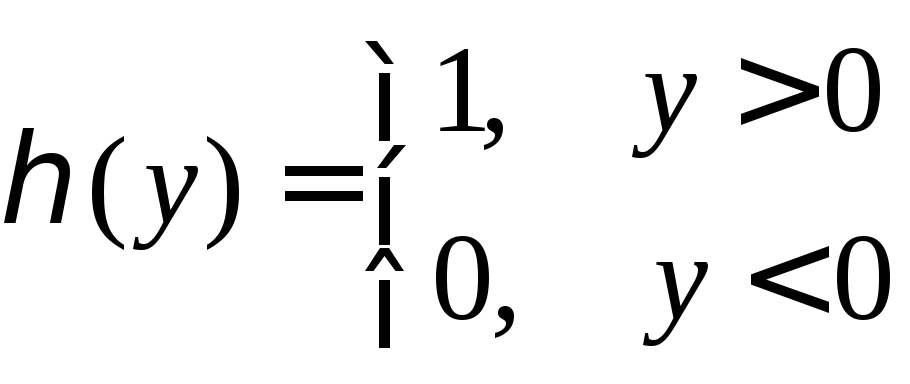 – функция
Хэвисайда.
– функция
Хэвисайда.
Итак,
![]()
![]() .
.
Пример 9.
Случайная
точка
![]() распределена равномерно внутри круга
радиуса
распределена равномерно внутри круга
радиуса
![]()
![]() Найти математическое ожидание случайной
величины
Найти математическое ожидание случайной
величины
![]() .
.
Решение. Плотность распределения вероятности
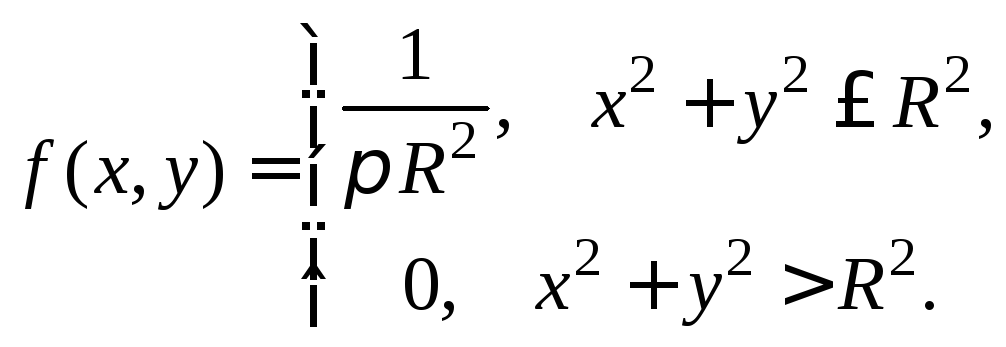
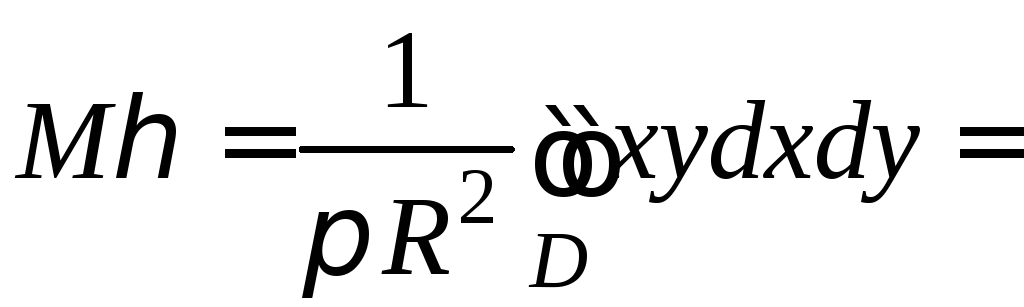
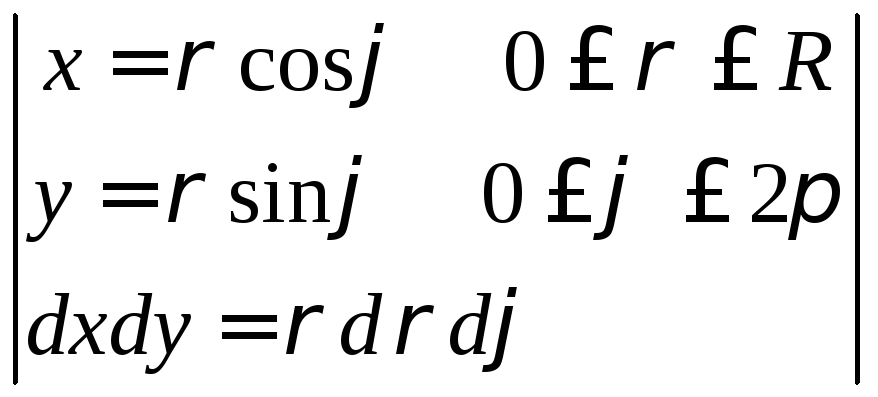 =
=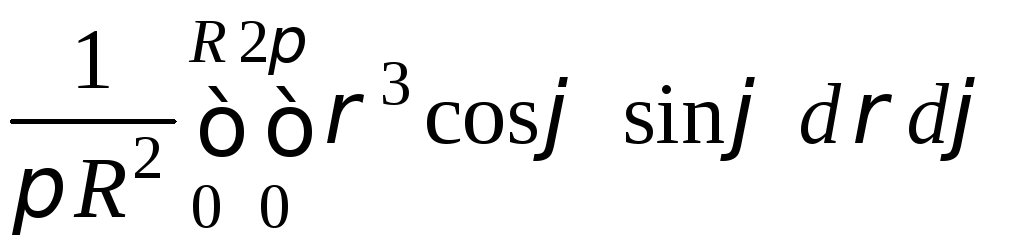 =
=
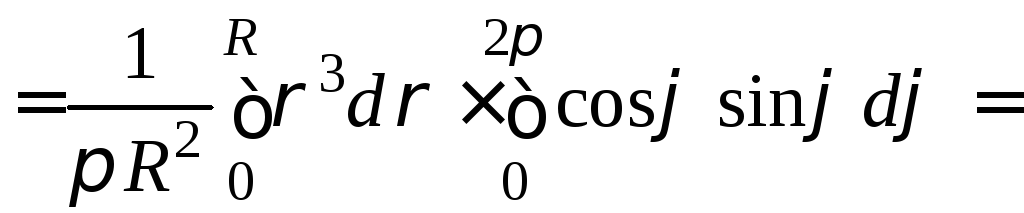
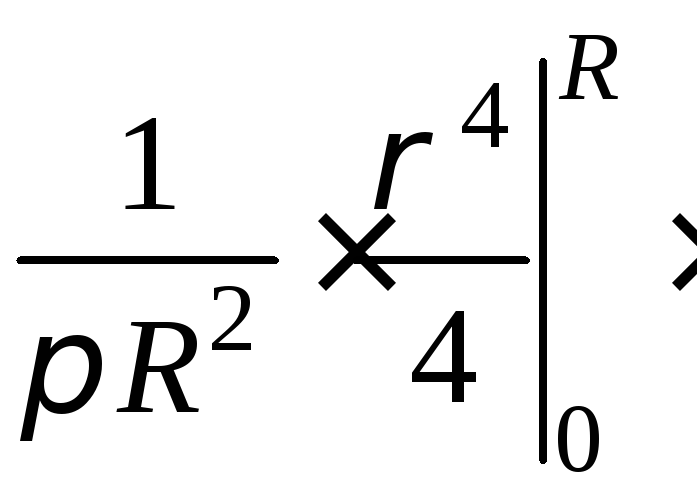
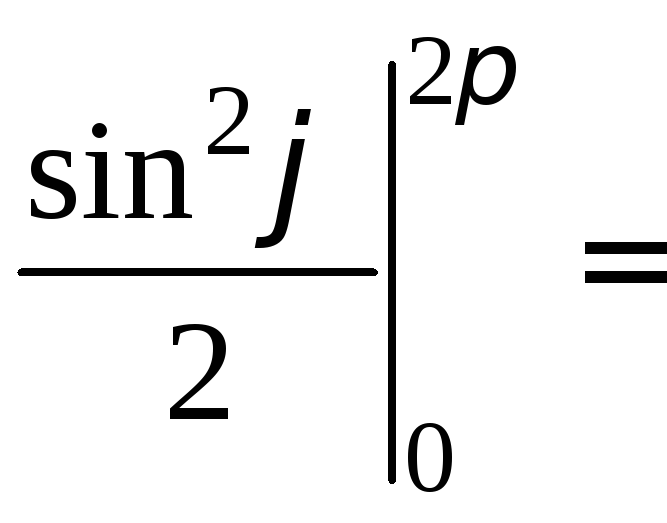
![]() .
.![]()
В приложениях часто используется следующая теорема.
Теорема. Пусть
![]() независимые случайные величины,
независимые случайные величины,
![]() Тогда
Тогда
![]() .
.
Замечание.
Здесь и в дальнейшем запись
![]() означает, что непрерывная случайная
величина
означает, что непрерывная случайная
величина
![]() имеет плотность распределения вероятности
имеет плотность распределения вероятности
![]()
![]() .
.
Замечание. Операция![]() называется сверткой функции f1
и f2.
называется сверткой функции f1
и f2.
Пример 10.
Независимые случайные величины
![]() имеют показательные распределения с
параметрами
имеют показательные распределения с
параметрами
![]() и
и
![]() .
Найти плотность распределения случайной
величины
.
Найти плотность распределения случайной
величины
![]() .
.
Решение. По
условию задачи случайные величины
![]() имеют плотности распределения
имеют плотности распределения
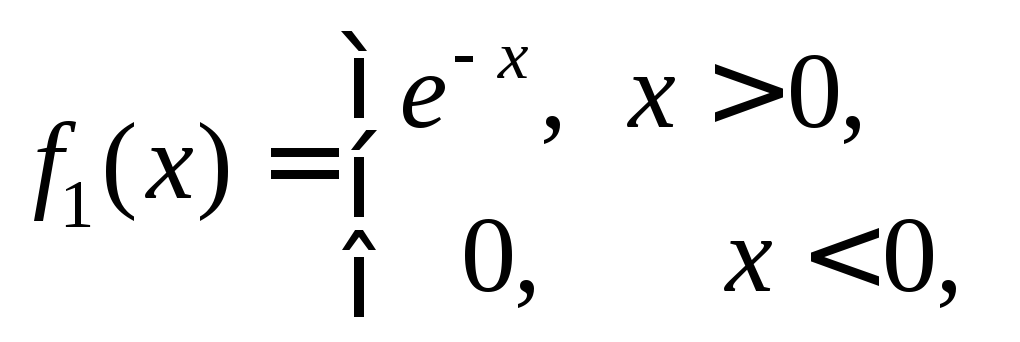 и
и
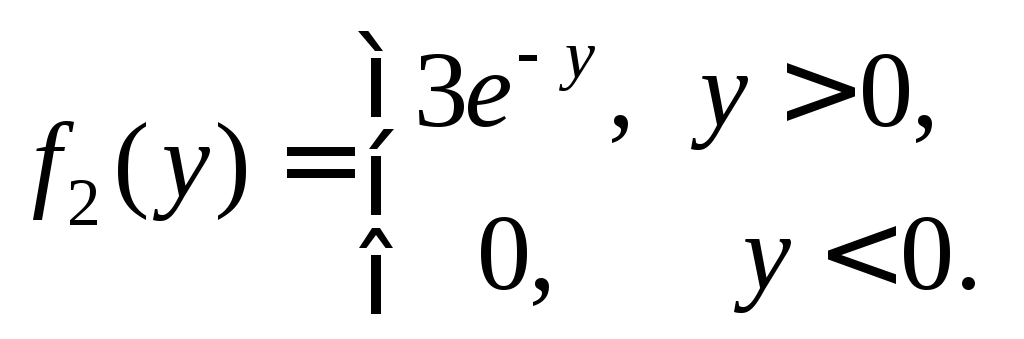
![]()
Так как случайные
величины
![]() независимы, то их совместная
плотность распределения
независимы, то их совместная
плотность распределения
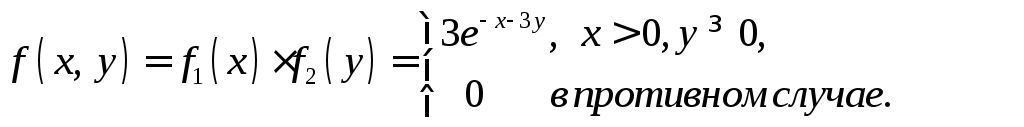
Случайная величина
![]() может принимать только положительные
значения, следовательно
может принимать только положительные
значения, следовательно

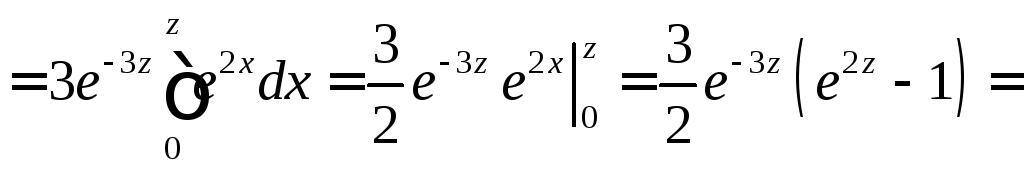
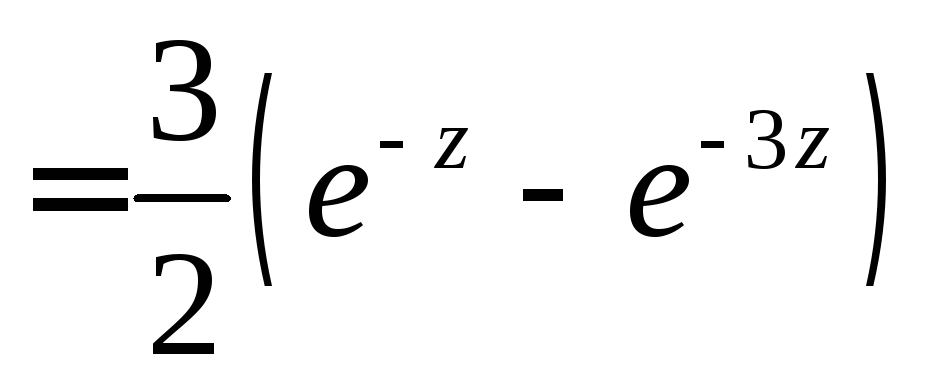 .
.
![]()
![]()
