11. Характеристические функции

Характеристической функцией случайной величины называется математическое ожидание случайной величины , , – вещественный параметр.

Для дискретной случайной величины .

Для непрерывной случайной величины с плотностью распределения

, .

Свойства характеристических функций

1) , .

2) , где – величина комплексно-сопряженная к .

3) Если , то .

4) Если – независимые случайные величины с характеристическими функциями , и , то .

5) Если существует , то

Примеры характеристических функций

Случайная величина распределена по биномиальному закону, тогда

, .

Случайная величина распределена по закону Пуассона с параметром , тогда

.

Случайная величина распределена по показательному закону

с параметром , тогда

.

Если .

Если .

Если – распределение Пирсона с n степенями свободы, то

.

Пример 1. Пусть принимает значения –1 и 1 с вероятностями каждое, имеет показательное распределение с параметром . Вычислить характеристические функции .

Решение. Характеристическая функция случайной величины , закон распределения вероятностей которой имеет вид

	–1	1

равна .

Характеристическая функция случайной величины равна

(т.к. то ).

Тогда, используя свойства характеристических функций, получим

,

где характеристическая функция случайной величины .

12. Закон больших чисел. Неравенство Чебышева

Пусть случайная величина имеет конечную дисперсию . Тогда для любого справедливо неравенство Чебышева

или

.

Теорема Чебышева

Пусть случайные величины независимы, существуют , и , , – некоторая постоянная.

Тогда для любого

.

В частности, если все имеют одно и то же математическое ожидание и дисперсию , то

.

Для биномиального распределения

.

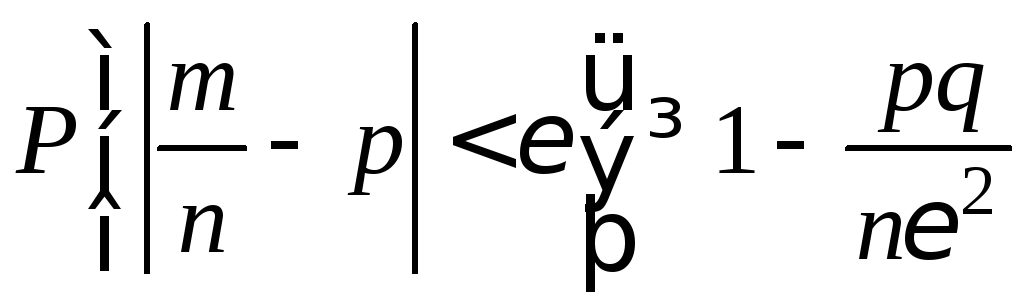Здесь – вероятность появления события в одном испытании, , – общее число испытаний, – число испытаний, в которых событие произошло.

Пример 1. При изготовлении некоторой детали брак равен 5%. Оценить вероятность того, что при просмотре партии в 2000 штук выявляется отклонение доли бракованных деталей от установленного процента брака меньше чем на 1%.

Решение. Воспользуемся формулой .

Здесь , , , .

Тогда .

Пример 2. Сколько нужно произвести измерений, чтобы с вероятностью, равной 0,95, утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,1, если .

Решение. Воспользуемся формулой .

Здесь , .

Имеем , , .

13. Квантили случайных величин

Пусть непрерывная случайная величина имеет функцию распределения , плотность распределения – и пусть задано число .

Определение. Квантилью уровня случайной величины называется такое число , что .

Рис. 4

Обозначим через квантиль уровня случайной величины ;

через – квантиль уровня распределения Пирсона с степенями свободы,  – квантиль уровня распределения Стьюдента с степенями свободы.

Свойства квантилей

1) , ;

2) если квантиль уровня случайной величины , то ;

3) при ;

4) ;

5) ;

6) для малых .