IV. Теория вероятности и математическая статистика Справочный материал и принципы решения задач

1. Классическое определение вероятности

Под опытом или экспериментом будем понимать всякое осуществление комплекса определенных условий, в результате которых будет происходить интересующее нас явление.

Будем считать фиксированным комплекс условий σ, который мы называем опытом, и будем рассматривать некоторую систему событий A, B, C,…, каждое из которых может либо произойти, либо не произойти.

Пример 1.  Опыт σ: стрельба по мишени. Событие А – попадание по мишени. Событие В – промах.

Пример 2. Опыт σ: выбор изделий из партии готовых. Событие А – изделие браковано. Событие В – изделие стандартное.

Элементарным событием (или элементарным исходом) называется любой простейший, то есть неделимый в рамках данного эксперимента, исход опыта. Множество всех элементарных исходов будем называть пространством элементарных событий и обозначать Ω. То есть множество исходов опытов образует пространство элементарных событий, если:

в результате опыта один из исходов обязательно происходит;

появление одного из исходов опыта исключает появление остальных;

в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.

Записывают это так:

Ω ={w_1, w_2, …w_n,…}={w_{k ,} k=1…n, …}.

Пример 3. Опыт: подбрасывание монеты 1 раз.

Здесь Ω={w_{г ,} w_ц}, где w_г – выпадение герба, w_ц – выпадение цифры.

Опыт: монета подбрасывается 2 раза. В данном случае пространство элементарных событий Ω={w_{г г,}w_{г ц ,} w_{ц г ,}w_{ц ц} }.

Опыт заключается в определении числа вызовов, поступивших на телефонную станцию за время Т. Здесь Ω={0,1,2.…n,… }.

Любой набор элементарных исходов или произвольное подмножество АΩ называетсяслучайным событием.

Пусть Ω  пространство элементарных событий, S  некоторое подмножество случайных событий, удовлетворяющее следующим условиям:

Множество S – замкнуто относительно операций сложения, умножения и отрицания.

.

Достоверное E и невозможное события принадлежатS.

Иногда требуют большего: для любой бесконечной последовательности событий

, .

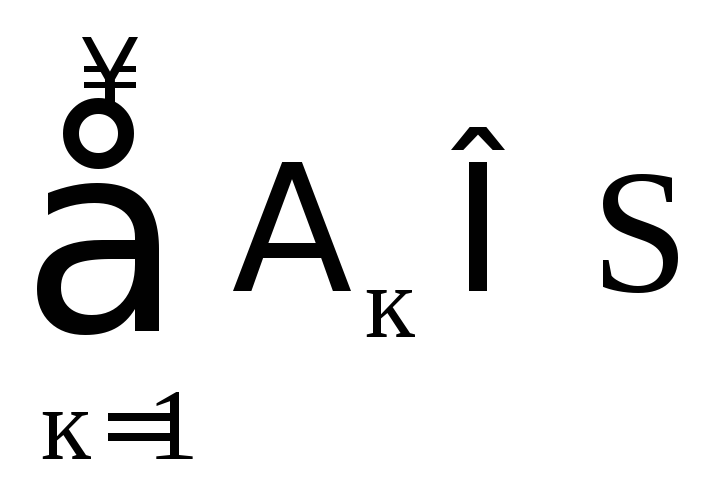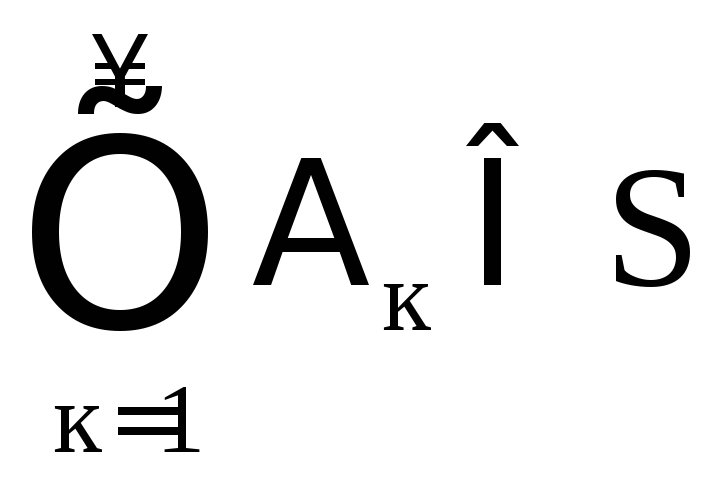Подмножество S, удовлетворяющее этим условиям, называется σ – алгеброй.

Пусть задана функция, которая каждому случайному событию из S ставит в соответствие число из интервала [0,1]; Р: S → [0,1], и при этом выполняются следующие аксиомы:

,

Р(Е)=1, Р(Ø)=0,

Для любой последовательности А₁,…А_n… попарно несовместных событий А_iS,

i,j, і≠ј,

.

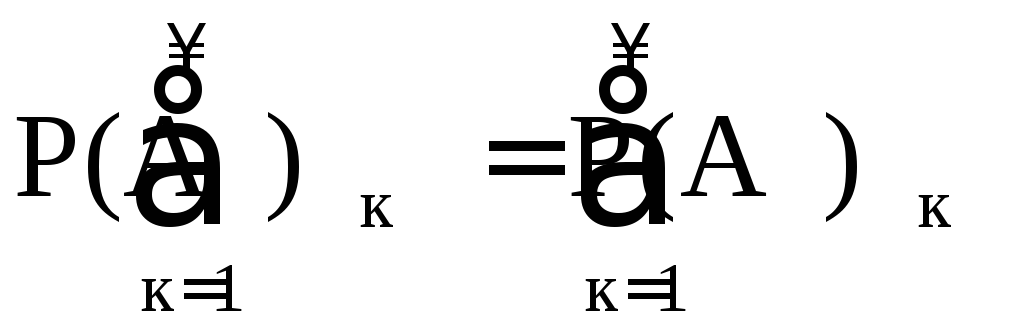Функцию Р, удовлетворяющую этим аксиомам, называют вероятностью, а значение Р(A) называют вероятностью события А.

Определение. Тройка объектов (Ω, S, Р), где Ω – пространство элементарных событий, S – σ-алгебра, Р – вероятность, называется вероятностным пространством.

Классическое определение вероятности служит хорошей математической моделью тех случайных явлений, для которых исходов опыта конечное число n и все исходы равновозможны. В классическом определении вероятности полагают:

;

вероятность события равной

.

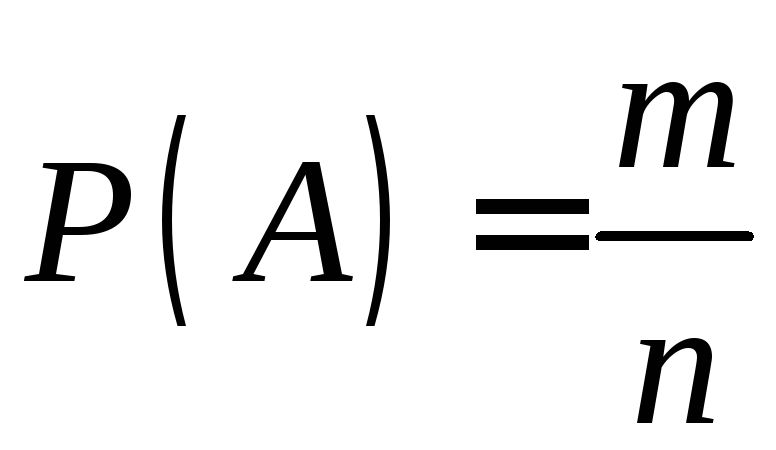Иными словами вероятность события равна отношению числа элементарных событий, входящих в, к общему числу элементарных событий в.

Общепринята так же следующая формулировка классического определения вероятности: вероятностью события называется отношение числа исходов опыта, благоприятствующих появлению события , к общему числу равновозможных исходов опыта.

То есть вероятность события определяется как.

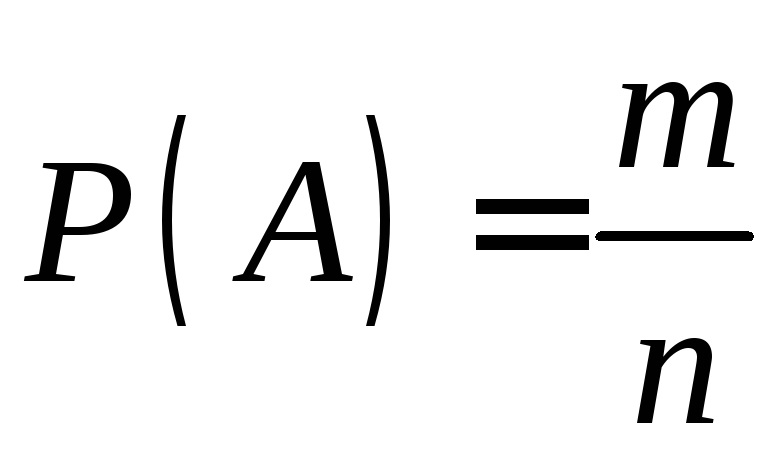Пример 4. Какова вероятность появления герба, по крайней мере, один раз при двукратном бросании монеты?

Решение.  Пространство равновозможных элементарных событий данного опыта состоит из следующих событий: Событие={при двукратном бросании монеты герб появится, по крайней мере, один раз} состоит из несовместных элементарных событий. Следовательно,.

Таким образом, .

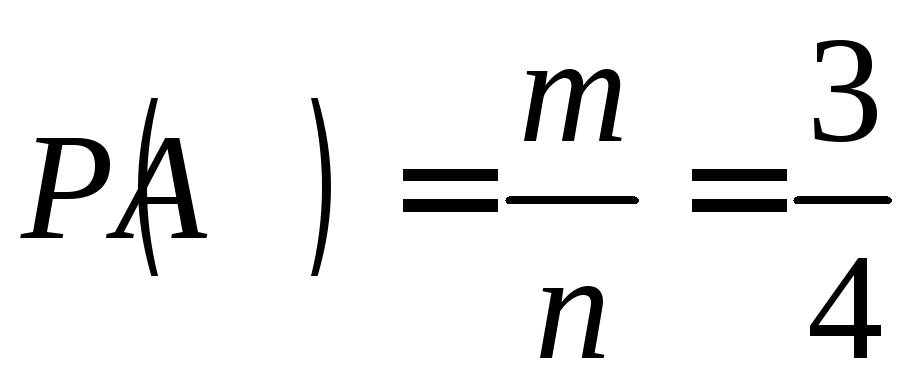Пример 5. Какова вероятность того, что случайно названное двузначное число будет делиться на одиннадцать без остатка?

Решение. Так как всех двузначных чисел 90, то число равновозможных исходов данного опыта . Из этих чисел на 11 без остатка делятся 11, 22, 33, 44, 55, 66, 77, 88, 99. Следовательно, число исходов, благоприятствующих событию {двузначное число будет делиться на одиннадцать без остатка}. Искомая вероятность будет равна.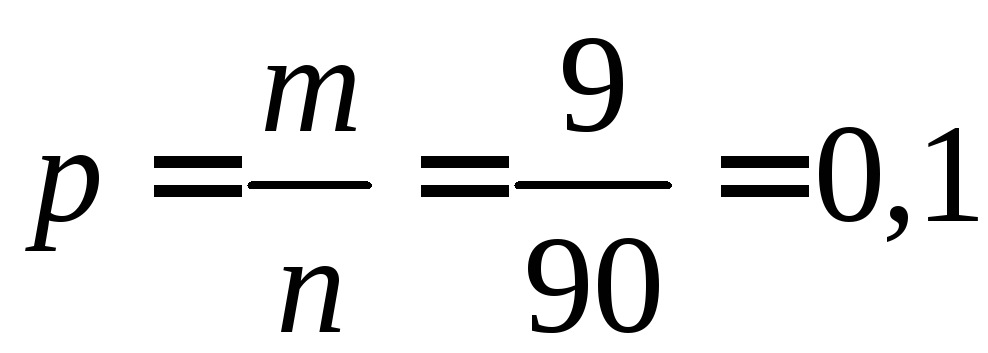

Пример 6. Какова вероятность того, что в сентябре наугад выбранного года окажется 5 воскресений?

Решение. В сентябре любого года 30 дней. Количество воскресений в сентябре зависит от того, какой день недели будет 1-е сентября. 1-е сентября может быть любым днём недели. Так как в неделе 7 дней, то и число всех возможных исходов . Если сентябрь начнется с понедельника, вторника, среды, четверга или пятницы то воскресений будет 4. Если сентябрь начнется с субботы или воскресенья, то воскресений будет 5. Среди 7 равновозможных исходов 2 будут благоприятны событию {в сентябре наугад выбранного года окажется 5 воскресений}, следовательно,. Искомая вероятность.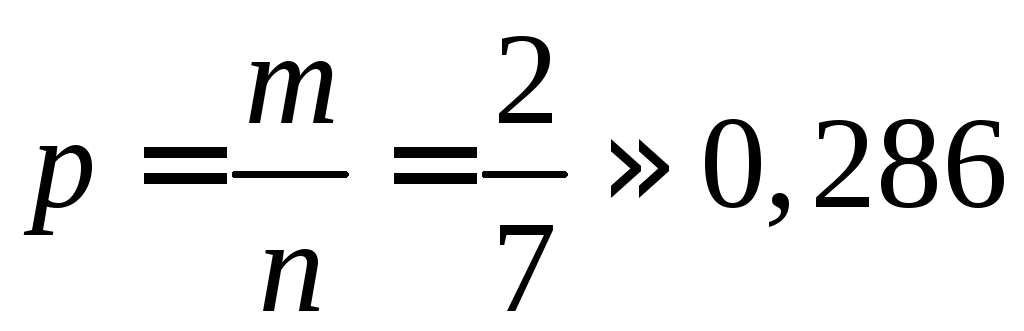

Пример 7. Имеются пять отрезков длиной 3, 5, 6, 9 и 11 см. Определить вероятность того, что из трех наугад взятых отрезков (из этих пяти) можно построить треугольник.

Решение. Имеется равновозможных исходов данного опыта:,,,,,,,,,.

Для того чтобы из трех отрезков можно было построить треугольник, необходимо, чтобы больший отрезок был меньше суммы двух других отрезков. Этому условию удовлетворяют следующие исходы ,,,,. Число таких исходов. Следовательно,

.

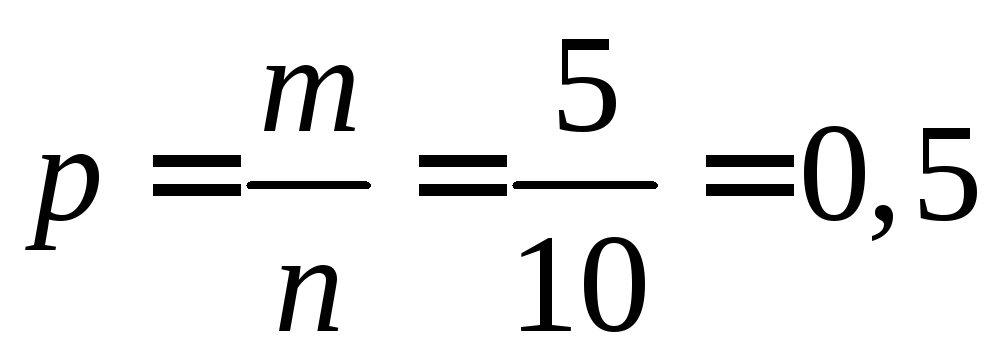В тех случаях, когда прямой перебор всех возможных исходов становится громоздким, целесообразно использовать комбинаторику.