9. Условный экстремум

Говорят, что функция u = f(x₁; x₂; . . .; x_n), определённая в некоторой окрестности точки , имеет в точке М условный максимум (условный минимум), если для любой точкиN(x₁; x₂; . . .; x_n) из вышеуказанной окрестности точки М, отличной от M, координаты которой удовлетворяют соотношениям

(6)

m < n, выполняется неравенство f(N) < f(M) (f(N) > f(M)), при этом считается, что координаты точки удовлетворяют уравнениям (6). Уравнения (6) называются уравнениями связи.

Для нахождения условного экстремума функции u = f(x₁; x₂; . . .; x_n) при уравнениях связи (6) (все рассматриваемые функции считаются дважды дифференцируемыми) вводят в рассмотрение функцию Лагранжа L(x₁; x₂; ...; x_n;) =f(x₁; x₂; ...;x_n) +(x₁; x₂;...;x_n)+ +(x₁; x₂; ... ; x_n) + ... + (x₁; x₂; ... ; x_n) и решают задачу нахождения экстремума функции L(x₁; x₂; ... ; x_n; ) при условии, что выполнены равенства

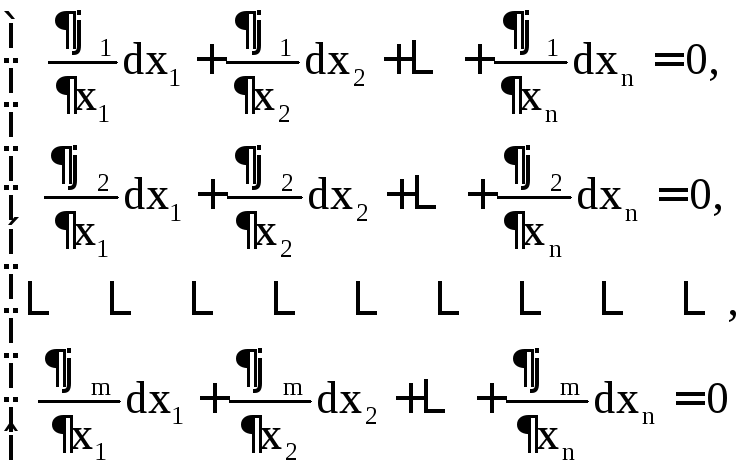(7)

для всевозможных наборов , для которых(есть приращение j - го аргументав точке М).

Теорема 6. Пусть – стационарная точка функции Лагранжа L(x₁; x₂; ... ; x_n; ). Если для всевозможных, подчинённых в точкеусловиям (7), справедливо неравенство

, то является точкой максимума, если для таких жетоявляется точкой минимума.

Замечание.  является квадратичной формой от переменных ; с учётом условий (10) число независимых переменных средиоказывается равным, что делаетквадратичной формой отнезависимых переменных. Вопрос знакопостоянства квадратичной формы можно решать с помощью критерия Сильвестра.

Пример 13. В полушар радиусом R вписать прямоугольный параллелепипед наибольшего объёма.

Решение. Обозначим через x, y, z измерения параллелепипеда: ,,. Пусть 0 – центр основания;. Тогда согласно теореме Пифагора

или

. (8)

Это есть уравнение связи. Обозначим левую часть уравнения (8) через . Фактически требуется решить следующую задачу на условный экстремум: найти наибольшее значение функции V = = xyz при условии, что переменные x, y, z удовлетворяют уравнению (8). Введём в рассмотрение функцию Лагранжа

.

Найдём стационарные точки функции :

, ,,.

Решим систему уравнений

Вычитая из первого уравнения, предварительно умноженного на x, второе, предварительно умноженное на y, получим . Учитывая особенности задачи (), заключаем, что. Действуя так же, находим, что. Отсюда получаем,,. Таким образом,или, если положить, является стационарной точкой функции.

Для выяснения того, является ли точкой экстремума, исследуем второй дифференциалпри условии, что в точке М dx, dy, dz связаны следующим соотношением (являющимся следствием равенства (8)):

;

;

.

Из последнего равенства получаем

(9)

Запишем формулу второго дифференциала функции , считая её функцией трёх переменныхx, y, z :

.

Имеем

,,,

,,,

,,.

.

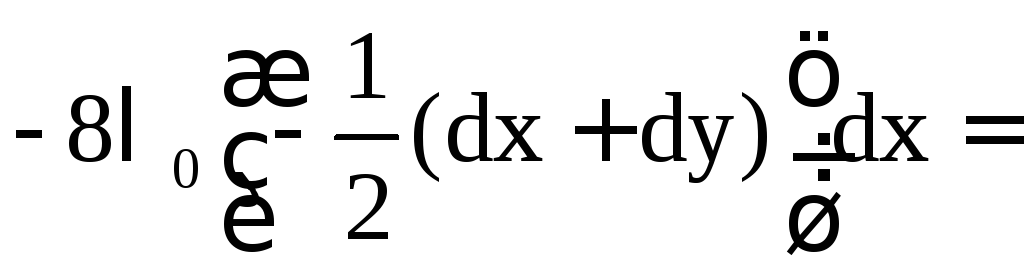
Так как выражение в квадратных скобках положительно при любых dx, dy, удовлетворяющих условию , а, то; следовательно, точкаявляется точкой условного максимума, и искомый параллелепипед имеет измерения,,, где x, y – измерения основания прямоугольного параллелепипеда, лежащего на круге полушара, а z – высота.

Замечание. Для решения вопроса знакопостоянства квадратичной формы в примере 19 можно было привлечь критерий Сильвестра. Образуем симметричную матрицу

.

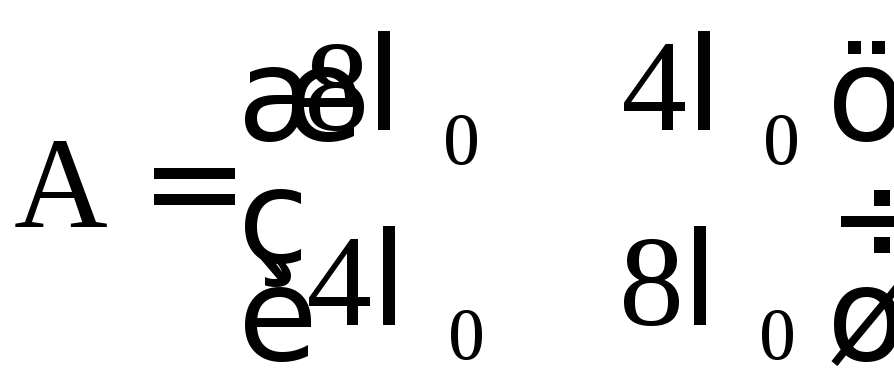Имеем

, ().

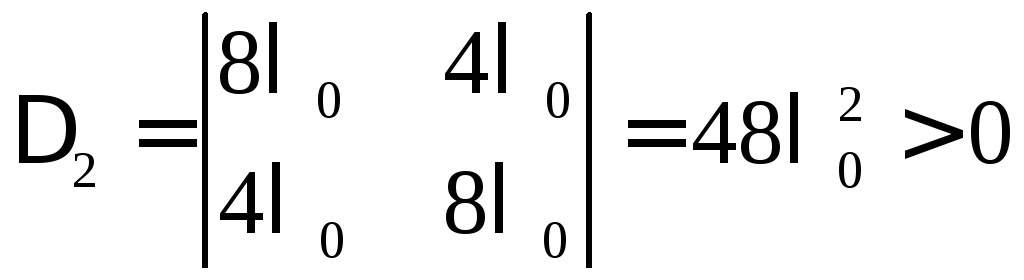Следовательно, отрицательно определён и поэтомуявляется точкой условного максимума.

В случае функции двух переменных справедливо следующее утверждение.

Теорема 7. Пусть требуется найти условный экстремум дважды непрерывно дифференцируемой функции u = f(x; y) с уравнением связи (x; y) = 0. Пусть – стационарная точка функции Лагранжа. Рассмотрим функцию

.

Тогда 1) если , тоявляется точкой условного минимума; 2) если, тоявляется точкой условного максимума.

Пример 14. Найти условный экстремум функции

при уравнении связи .

Решение. Составим функцию Лагранжа

.

Найдём стационарные точки этой функции

, ,.

Решим систему уравнений

Решив систему, находим ,,. Имеем,,,.

, следовательно, является точкой условного максимума.