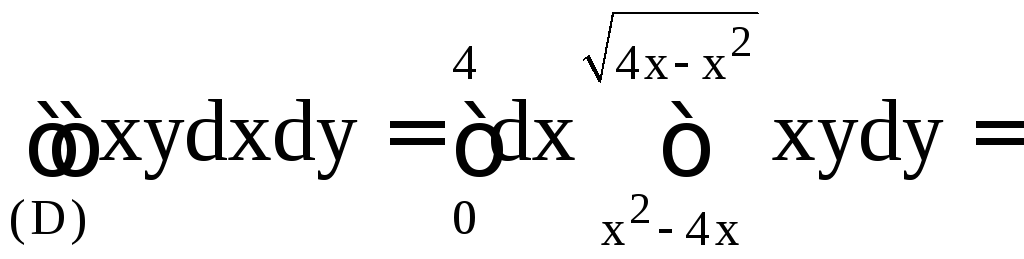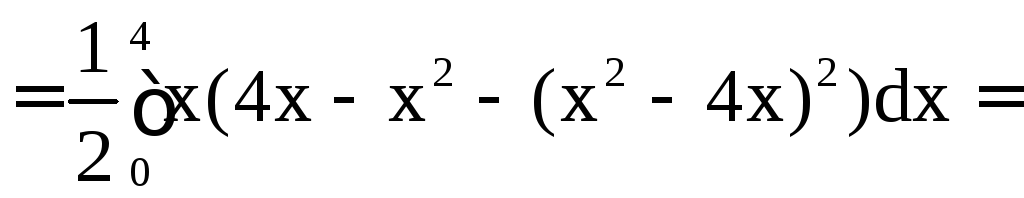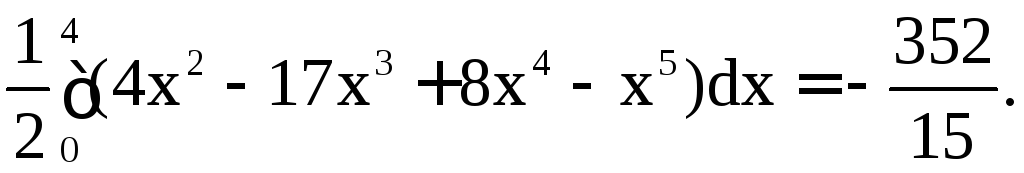IX. Кратные интегралы

1. Двойной интеграл

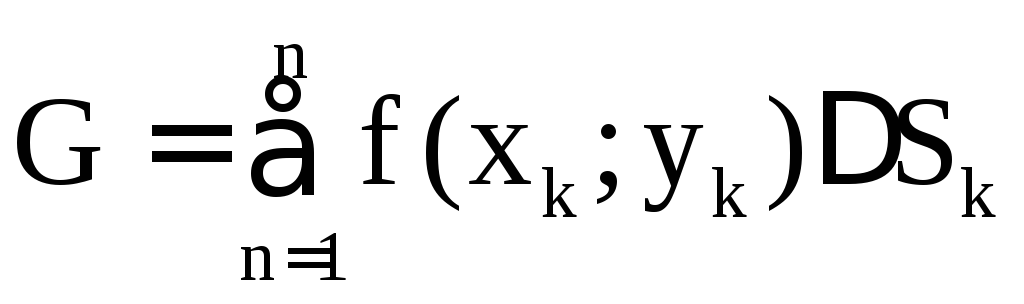Пусть функция f(x;y) определена в замкнутой ограниченной области (D)R². Разобьем эту область на частичные области (D₁), (D₂),, (D_n), площади которых равны S₁, S₂,, S_n соответственно. Обозначим через d_k диаметр области (D_k) d_k = sup{MM; M,M(D_k)}. Число называется диаметром разбиения. В каждой частичной области (D_k) возьмем по точке М_k(x_k;y_k). Выражение называется интегральной суммой функцииf(x;y) по области (D). Если существует конечный предел интегральных сумм G при 0, предел, не зависящий ни от способа разбиения, ни от выбора точек М_k, то этот предел называется двойным интегралом от функции f(x;y) по области (D) и обозначается

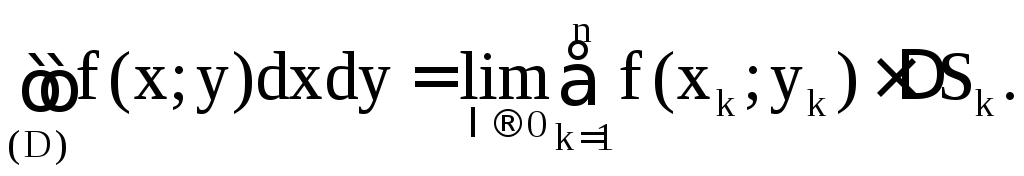
При этом говорят, что f(x;y) интегрируема в (D).

Для интегрируемости f(x;y) в ограниченной замкнутой области (D) достаточно, чтобы f(x;y) была непрерывна в (D).

Теорема 1. Если f(x;y), g(x;y) интегрируемы в (D), то k₁f(x;y)+k₂g(x;y) также интегрируема в (D) и при этом

Теорема 2. Если f(x;y) интегрируема в области (D), и пусть площадь множестваравна нулю. Тогда

Вычисление двойного интеграла сводится к вычислению повторного интеграла. Если f(x;y) непрерывна в замкнутой области (D) и (D) ограничена непрерывными линиями y = (x), y = (x), x = а, x = b, (x)(x) при

а  x  b, то

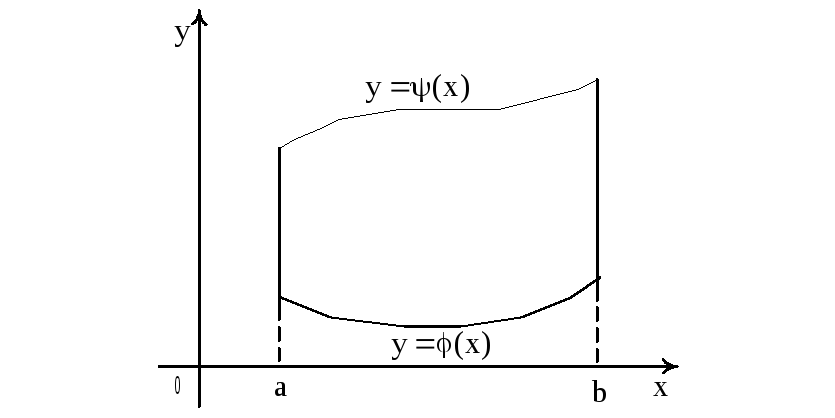
Правая часть последнего равенства обычно записывается иначе:

Иногда удобно производить внешнее интегрирование по y, внутреннее – по x: если (D) ограничена линиями x = (y), x = (y), y = c, y = d,

(y)  (y) при y c,d, то

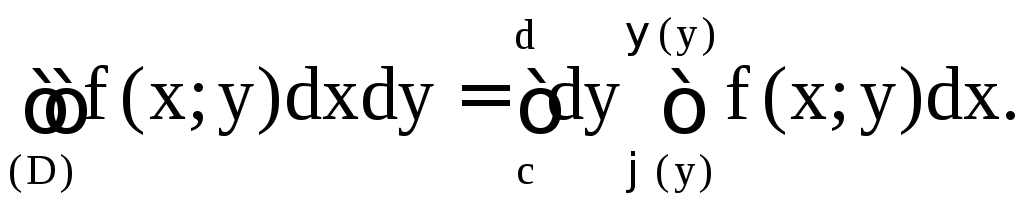
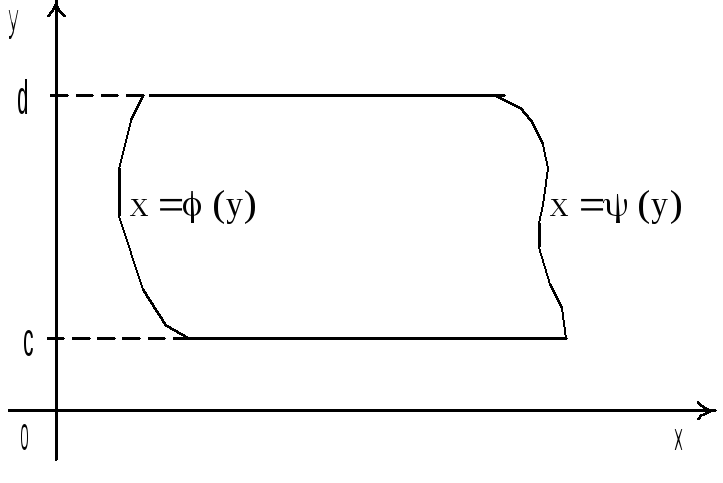
В случае, если область (D) имеет сложный вид, то ее разбивают на простые подобласти и применяют теорему 2.

Пример  1. Область (D) задана неравенствами :

а) построить область (D);

б) записать двойной интеграл в виде повторного;

в) изменить порядок интегрирования в повторном интеграле.

Решение. а) Уравнение определяет параболу с вершиной в точке, уравнение– верхнюю полуокружность окружности.

В самом деле, уравнение эквивалентно системе

или 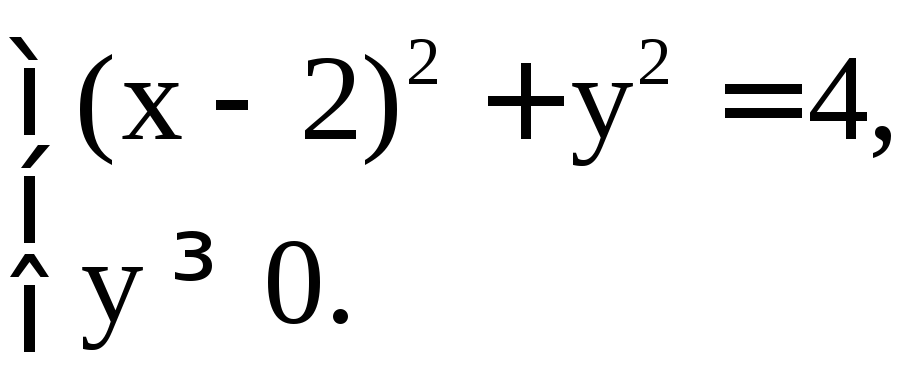. Сделаем рисунок. Область (D) заключена между параболой и полуокружностью.

б) Найдем пределы изменения переменного x – проекции (D) на ось 0x. Для этого составим и решим уравнение

Отсюда находим ,. Таким образом,x пробегает все значения из отрезка 0;4. При каждом фиксированном значении x₀0;4 прямая пересекает область (D) по отрезку, тянущемуся от точки параболы с абсциссой x₀ до точки полуокружности с той же абсциссой. Поэтому область (D) определяется системой неравенств:

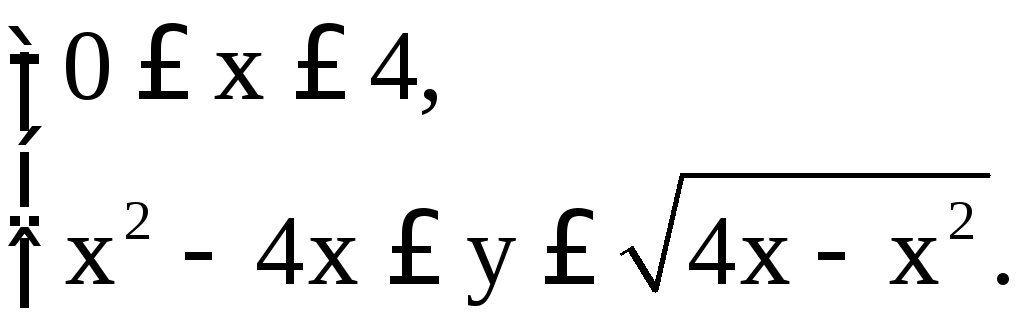
Следовательно

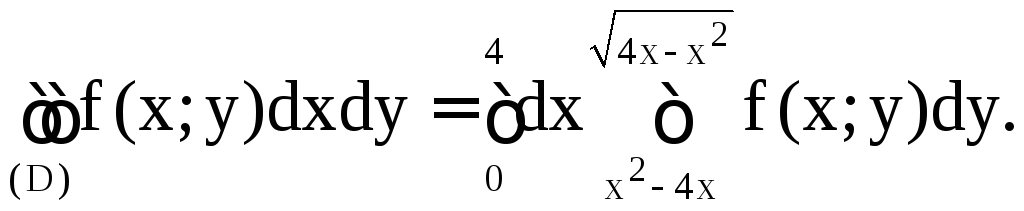
в) Изменим порядок интегрирования, приняв в качестве внешнего переменного y, внутреннего – x. Составим уравнения линий, ограничивающих (D), выразив x через y. Для уравнения окружности получим: ,,,левая полуокружность,правая полуокружность. Для уравнения параболы:левая ветвь параболы,правая ветвь параболы. Переменноеy меняется в целом от –4 до 2. Покуда y меняется в пределах от –4 до 0, x меняется от абсциссы соответствующей точки левой ветви параболы до абсциссы соответствующей точки правой ветви параболыЕсли жеy меняется в пределах отрезка [0;2], то x меняется от абсциссы соответствующей точки левой полуокружности до абсциссы соответствующей точки правой полуокружностиТаким образом, если считать область (D) разбитой на две части: (D₁) – ниже от 0x и (D₂) – выше от 0x, то пределы изменений переменных можно выразить следующими неравенствами:

для (D₁):

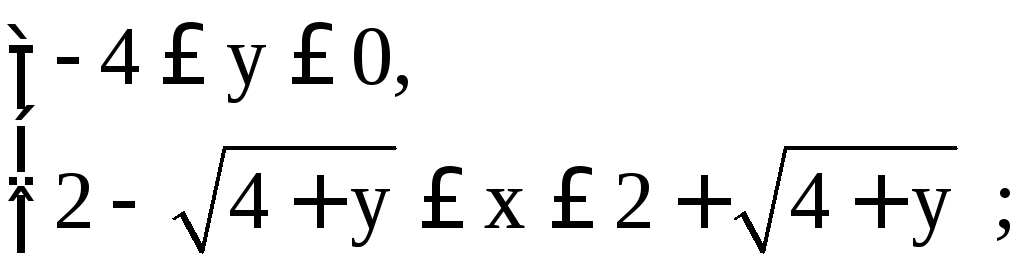
для (D₂):

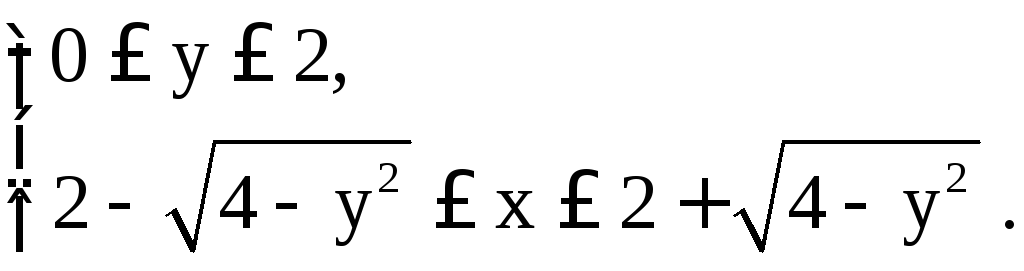
Эти соображения приводят к следующему представлению двойного интеграла:

Пример 2. Вычислить двойной интеграл где (D) – область из примера 1.

Решение. Имеем