5. Уравнение касательной плоскости и нормали к поверхности

Если поверхность задана уравнениеми– дифференцируемая функция, то уравнение касательной плоскости, проведённой к поверхности () в точке, имеет вид

.

Уравнение нормали к этой поверхности в той же точке имеет вид

.

В частности, если уравнение поверхности задано в явной форме , то уравнение касательной плоскости к поверхности в точкеможет быть задано в виде

,

а уравнения нормали –

.

Пример 7. Составить уравнения касательной плоскости и нормали к поверхности в точке M(2; –1; 1).

Решение. Обозначим . Имеем

, ,

, ,

, .

Отсюда находим уравнение касательной плоскости

9(x – 2) + 14(y + 1) – 3(z – 1) = 0

или

9x + 14y – 3z–1 = 0

и уравнения нормали

.

6. Дифференцирование сложной функции

Пусть – дифференцируемая функция отn переменных и пусть переменные, в свою очередь, являются дифференцируемыми функциями от переменных:

Тогда     становится дифференцируемой функцией от переменныхи при этом

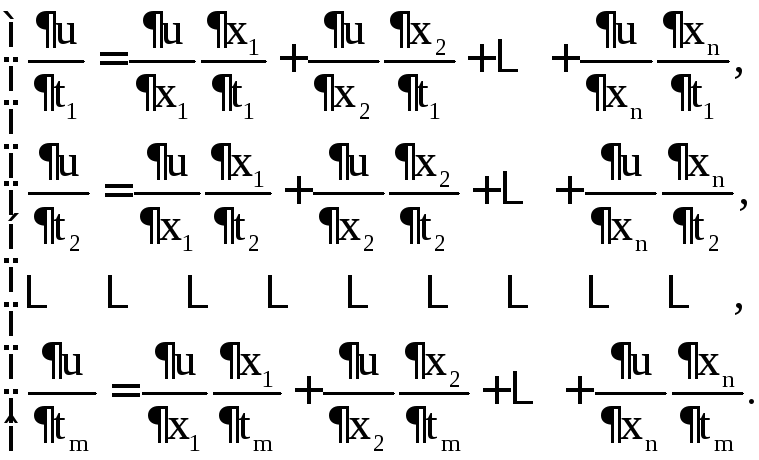
В частности, если зависят от одного переменного t , то u становится функцией от одного переменного t и

.

Пример 8. Найти , если,,.

Решение. Имеем

, ,

, ,,.

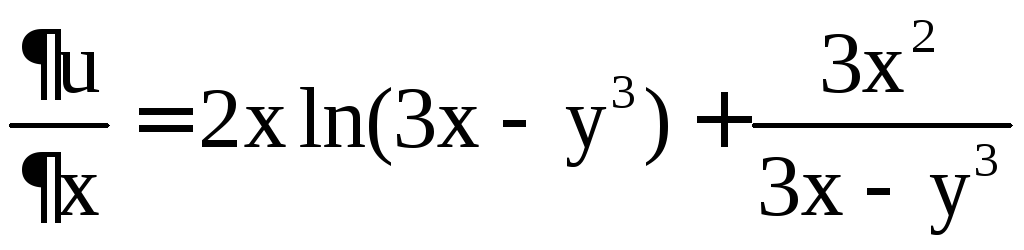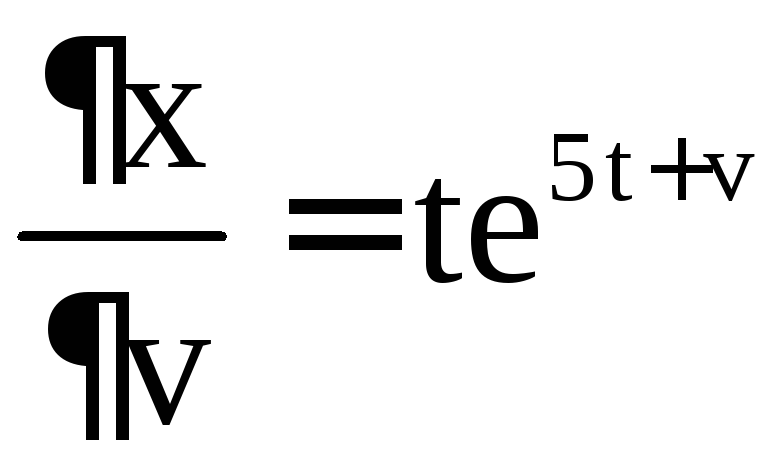Отсюда получаем

,

.

7. Дифференцирование неявно заданной функции

Пусть функция F(x; y) определена в области (D) и (a; b), (c, d) – проекции (D) на оси 0x и 0y соответственно. Говорят, что уравнение

F(x; y) = 0 (2)

в области (D) задаёт неявную функцию y = f(x) , если для любого уравнениеимеет единственное решение(это решение и является правилом задания функции: каждомуставится в соответствие решение уравнения F(x; y) = =0 ).

Если уравнение (2) в (D) задаёт неявную функцию ,

F(x; y) дифференцируема в (D) и , тодифференцируема и

.

Вторая производная находится повторным дифференцированием последнего равенства.

Пример 9. Найти , если.

Решение. Обозначим левую часть уравнения через F(x; y). Тогда

.

Аналогично определяется неявная функция многих переменных. Пусть функция определена в областии– проекции (D) на n-мерную координатную плоскостьи на ось 0u соответственно. Говорят, что уравнение

(3)

задаёт в (D) неявную функцию , если для любой точкиуравнениеимеет единственное решение. Если уравнение (2) в области (D) задаёт неявную функцию,дифференцируема в (D) ивсюду в (D), то функцияявляется дифференцируемой и

.

Пример 10. Найти , если

.

Решение. Обозначим через F(x; y; z) левую часть уравнения. Имеем

,

.

Подобным образом определяются системы неявных функций. Пусть дана система из m уравнений с (n + m) переменными

(4)

и функции определены в области (D)-мерного пространства. Пусть– проекция (D) на координатную плоскость, () – проекция (D) на координатную плоскость. Если для любой точкисистема уравнений

имеет единственное решение , такое что, то говорят, что система (4) задаёт неявные функции

, , ....

Решение системы (4) относительно и является правилом задания функции: каждомуставится в соответствие решение,     ,..., системы (4).

8. Экстремум функции многих переменных

Пусть функция определена в некоторой окрестности точки. Говорят, что точка М является точкой максимума (минимума) функции, если существует окрестность V точки М, такая что для любой точки N из этой окрестности V, отличной от точки М, справедливо неравенство f(N) < f(M) (f(N) > f(M)). Точки максимума и точки минимума функции называют точками экстремума функции, а значения функции в этих точках – экстремумами функции.

Теорема 3 (необходимое условие экстремума). Если М – точка экстремума дифференцируемой функции , то

. . . . (5)

Точка М, в которой выполнены условия (5), называется стационарной точкой. Не любая стационарная точка функции является точкой экстремума. Cледующая ниже теорема даёт достаточное условие для того, чтобы стационарная точка функции двух переменных была точкой экстремума.

Теорема 4 (достаточное условие экстремума для функции двух переменных). Пусть – стационарная точка функции двух переменных u = f(x; y), дважды непрерывно дифференцируемой в некоторой окрестности точки М.

Рассмотрим определитель

.

1) Если , тоявляется точкой экстремума функции u(x; y) = f(x; y), а именно: а) если, то М – точка минимума; б) если, то М – точка максимума.

2) Если , то М не является точкой экстремума.

Пример 11. Найти точки экстремума функции

.

Решение. Найдём стационарные точки функции ,. Решим систему уравнений

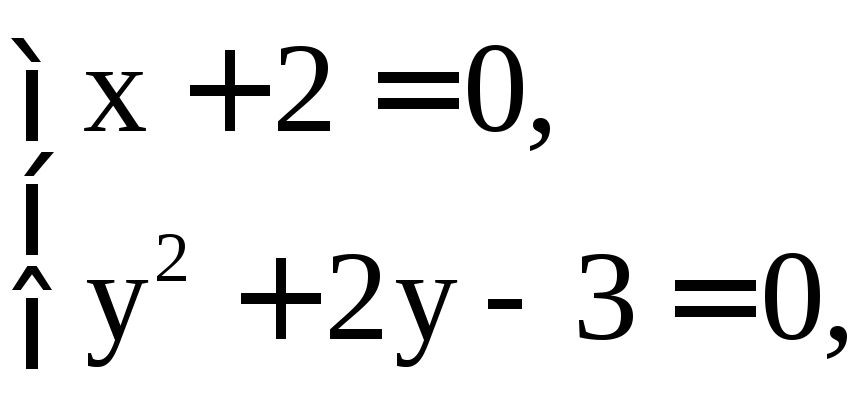
Решением системы являются точки M₁(–2; –3), M₂(–2; 1). Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:

, ,.

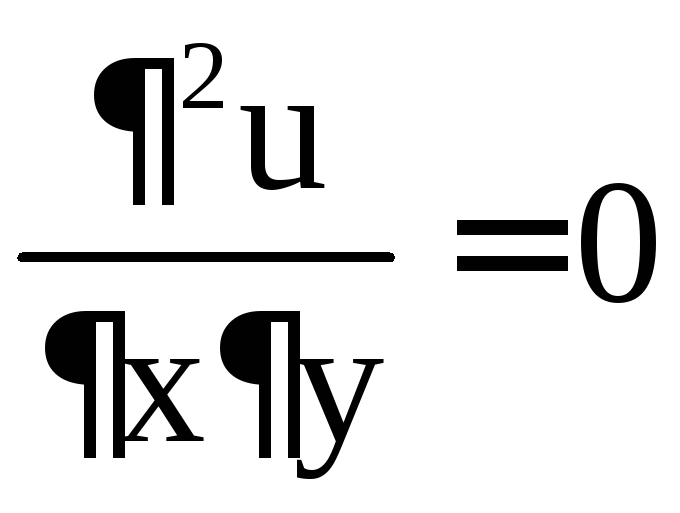Имеем

.

, следовательно, M₁(–2; –3) не является точкой экстремума.

, что говорит о том, что M₂(–2; 1) является точкой экстремума. А так как , то заключаем, что M₂ – точка минимума.

Теорема 5 (достаточное условие экстремума для функции трёх переменных). Пусть – стационарная точка функции

, дважды непрерывно дифференцируемой в некоторой окрестности точки М. Рассмотрим определители

, ,

.

Пусть . Тогда имеем:

a) если , то– точка минимума;

б) если , то– точка максимума;

в) во всех остальных случаях (при условии ) М не является точкой экстремума.

Пример 12. Найти точки экстремума функции

.

Решение. Найдём стационарные точки функц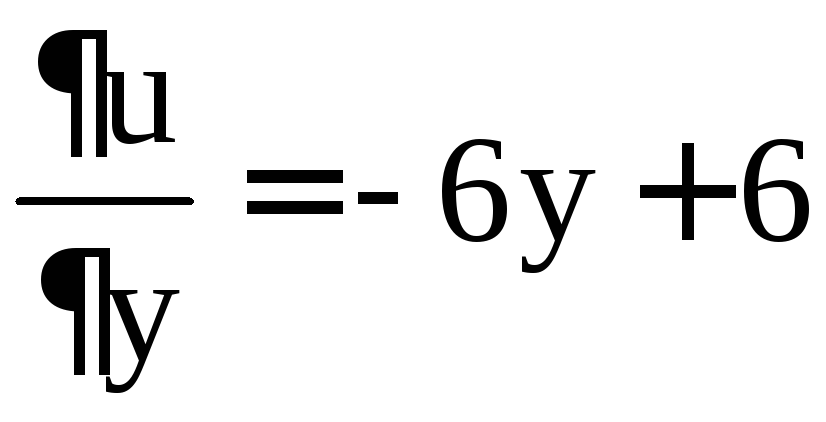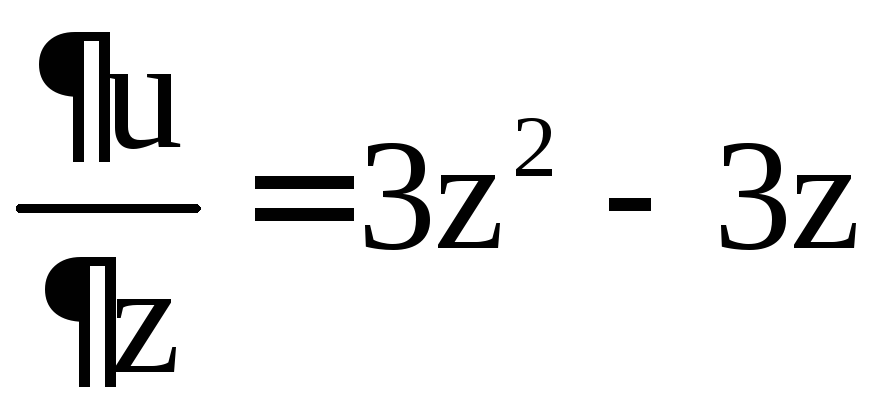ии ,,. Решим систему уравнений

Решение этой системы приводит к двум стационарным точкам

M₁(–2; 1; 0) и M₂(–2; 1; 1). Проверим, являются ли эти точки точками экстремума.

–2, ,,,,.

, ,

.

.

Следовательно, является точкой максимума.

, что означает, что не является точкой экстремума.

Аналог теоремы 5 справедлив и для функции u = f(x₁; . . .; x_n) n переменных, n > 3.