3. Частные производные

Пусть функция определена в некоторой окрестности точки. Придадим переменномуx_k в этой точке приращение . Тогда функция получит приращение

.

Конечный предел (если он существует)

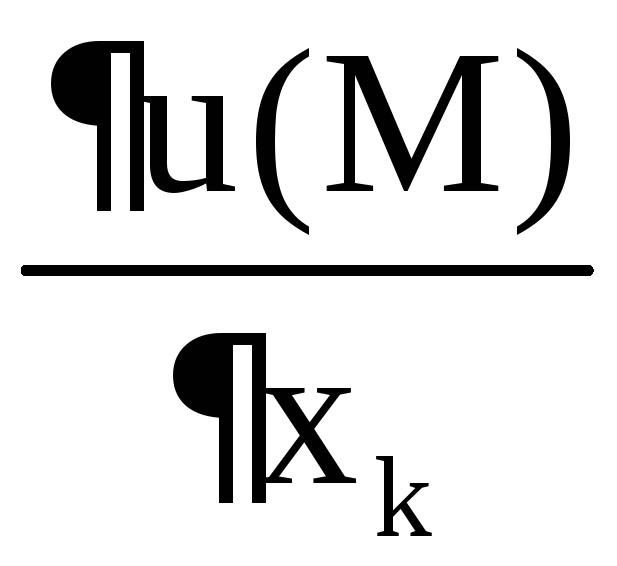называется частной производной (первого порядка) функции по переменному x_k в точке и обозначаетсяилиили. Процесс нахождения частной производной называют дифференцированием функции.

Для частных производных справедливы те же правила дифференцирования, что и для функции одного переменного (формулы производной суммы, произведения и т.п.).

При нахождении частной производной по переменному x_k следует действовать так, как если бы все остальные переменные являлись постоянными величинами.

Пример 3. Найти 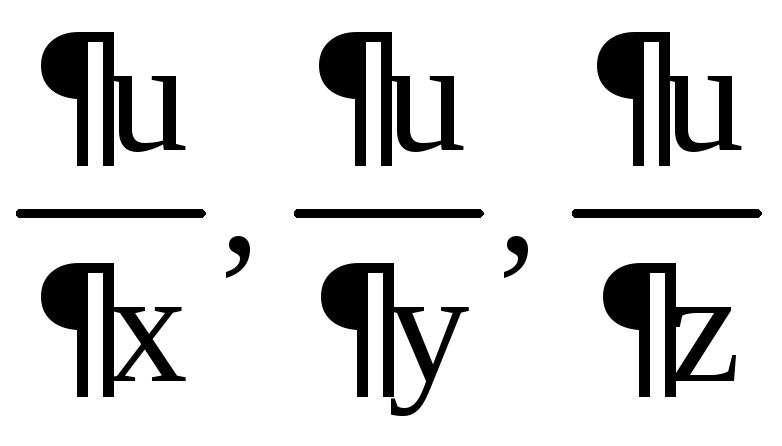для функции. Найти.

Решение.

;

;

.

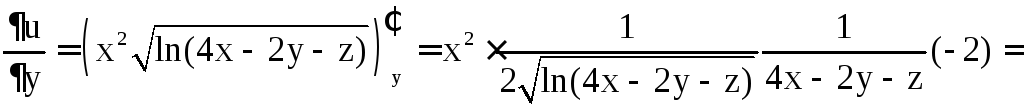
Из последнего равенства находим

.

Частная производная от частной производной первого порядка называется частной производной второго порядка. Приняты следующие обозначения частных производных второго порядка функции :

.

Аналогично определяются частные производные более высоких порядков.

Пример 4. Найти все частные производные второго порядка функции . Найти.

Решение. ,,,

;

;

;

;

;

;

;

;

(1; –1; 2) = 4 – 32⁴ = 4 – 48 = – 44.

Возникает естественный вопрос: зависят ли частные производные высших порядков от порядка дифференцирования (в последнем примере мы видели, что ,,). Оказывается, что, вообще говоря, смешанные производные зависят от порядка дифференцирования. Однако справедливо следующее утверждение.

Теорема 1. Если все частные производные функции до m-го порядка включительно непрерывны, то смешанные производные m-го порядка не зависят от порядка дифференцирования.

Пример 5. Показать, что функция удовлетворяет уравнению колебания струны.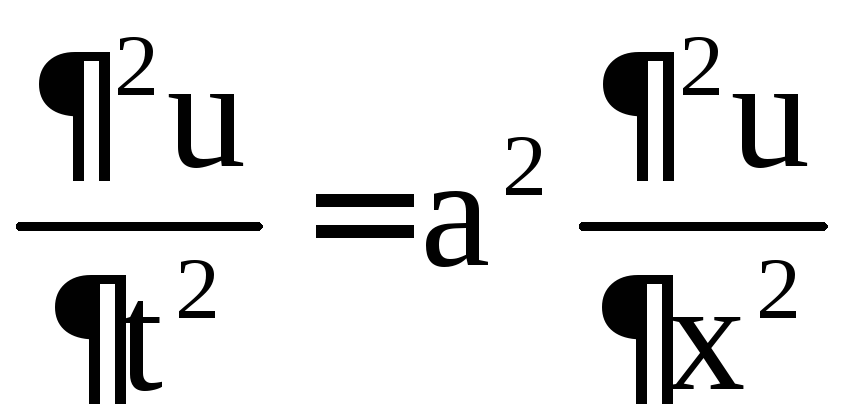

Решение. Имеем ;

;

; .

Сравнивая полученные выражения, видим, что .

4. Дифференциал функции многих переменных

Пусть функция определена в некоторой окрестности точки. Придадим переменнымв этой точке приращения. Тогда функция получит (полное) приращение

.

Функция называется дифференцируемой в точке, если существуют числаA₁, A₂, ... ,A_n, такие что

(1)

при ,

где

. (Числа A₁, A₂, ... , A_n не зависят от .)

Если имеет непрерывные частные производные первого порядка по всем переменным, то она дифференцируема, причём,, . . . ,.

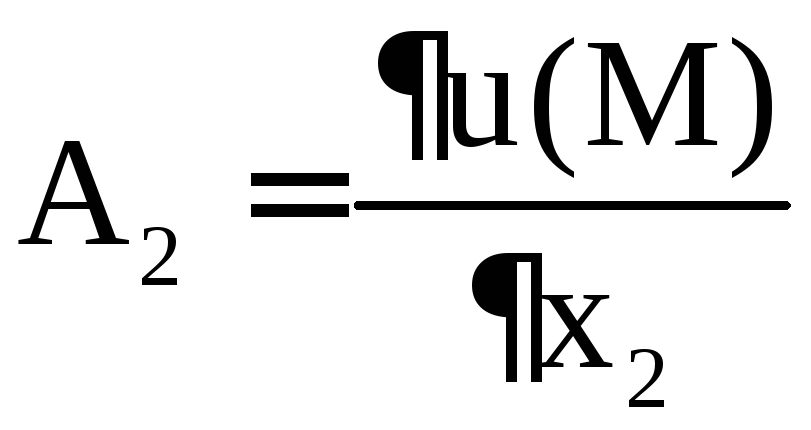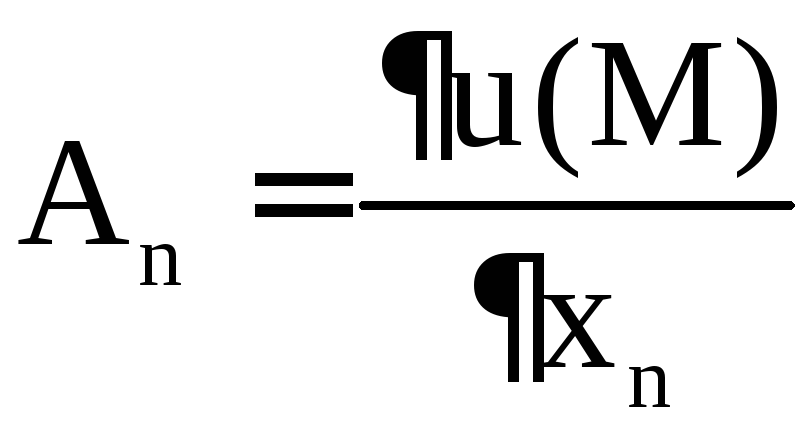Линейная часть приращения функции называется дифференциалом (первого порядка) функции и обозначается

или просто

.

Если являются независимыми переменными (т.е. не зависят от других переменных), то полагают дифференциалы этих переменных равными их приращениям:. С учётом этого, а также того, что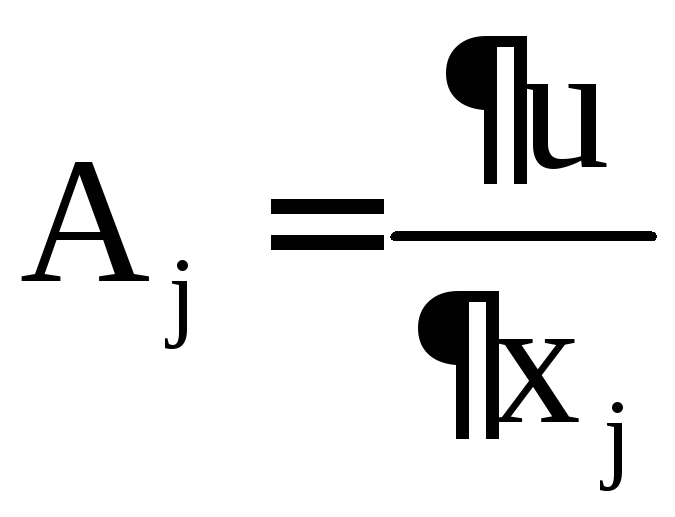, получаем

.

В частности, для функции двух переменных

.

Для дифференциала функции многих переменных справедливы те же правила, что и для функции одного переменного: ,,.

Дифференциал от первого дифференциала функции называется дифференциалом второго порядка и обозначается:. Аналогично определяются дифференциалы более высоких порядков:,и т.д.

Если все частные производные функции до m-го порядка включительно непрерывны, аявляются независимыми переменными, то дифференциал m-го порядкавыражается символической формулой

.

При этом выражение в скобках раскрывается по формуле бинома Ньютона, а затем перед множителями над чертой дописывается буква u. Например, для функции двух переменных

,

.

Для функции трёх переменных

Следует иметь в виду, что под понимаются квадраты дифференциалов, а не дифференциалы квадратов:,,.

Пример 6. Найти du и d²u для функции .

Решение. , ;

.

, ,.

.